Презентация "Применение правильных многогранников" по математике – проект, доклад
Презентацию на тему "Применение правильных многогранников" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 19 слайд(ов).
Слайды презентации
Список похожих презентаций
Мир правильных многогранников
Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, ...Элементы правильных многогранников
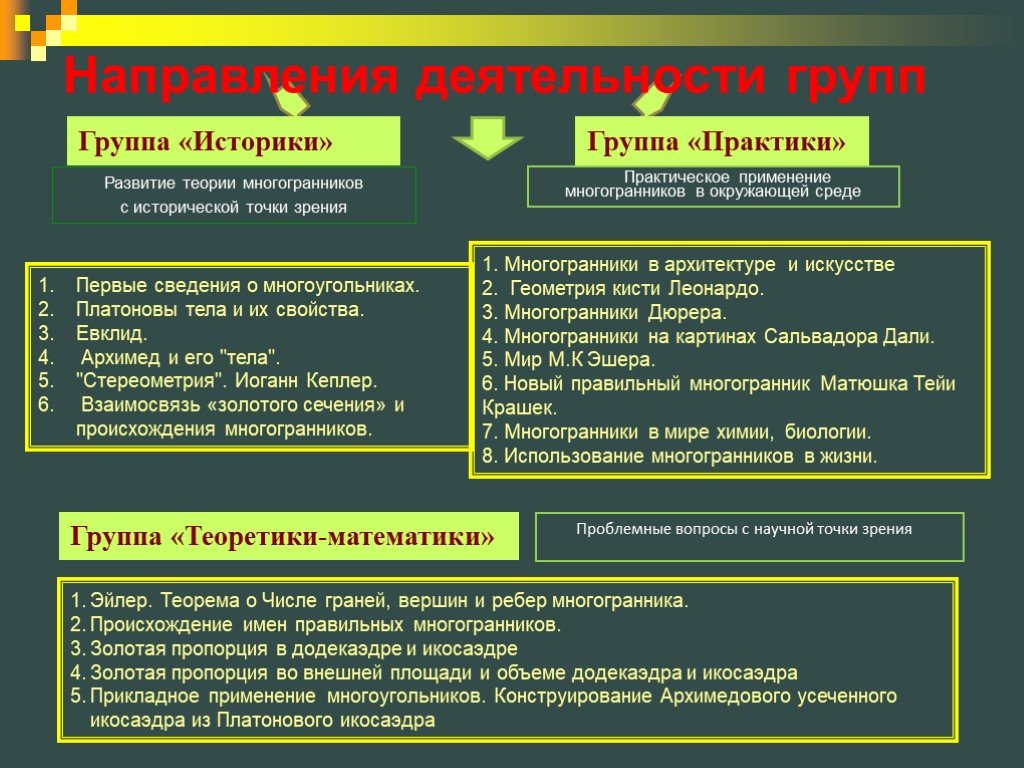
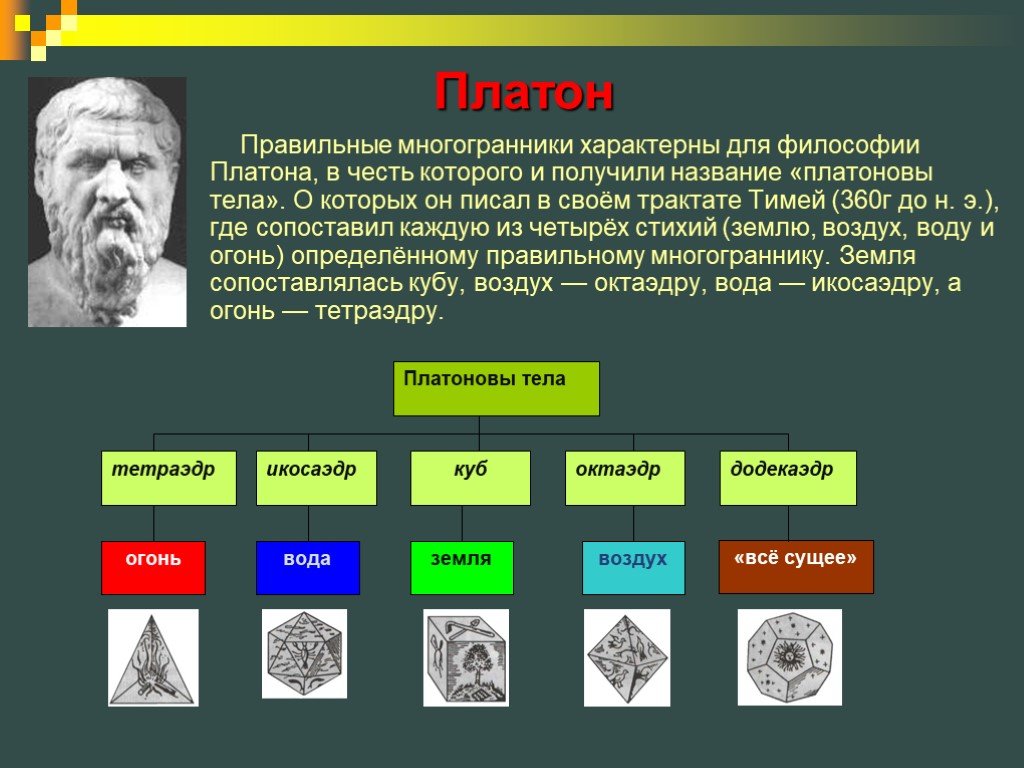
Содержание:. Цель пректа Термин Многогранники История Платон Платоновы тела Евклид Архимед Архимедовы тела Иоганн Кеплер Космологическая гипотеза ...Классификация и свойства правильных многогранников
Свойства многогранников Многогранники представляют собой простейшие тела в пространстве. Многогранные формы мы видим ежедневно: спичичный коробок, ...Виды правильных многогранников
Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук. Л. Кэрролл. ...Применение свойств действий с рациональными числами
С каким настроением я начинаю урок? хорошее среднее плохое. Рациональные числа. Числа, которые можно представить в виде отношения - натуральное число, ...Применение распределительного свойства умножения
Цели урока:. Закрепить навыки применения распределительного свойства умножения для упрощения выражений и устного счета. Проверка выполнения домашнего ...Применение производной к исследованию функций
Цель урока – закрепить и систематизировать знания учащихся по исследованию функций с помощью производной. Применение производной к исследованию функции. ...Применение производной к исследованию и построению графиков функций
Цель урока:. научиться применять таблицу производных при исследовании функций и построении графиков. Математический диктант. Вариант 1. (Cu)’=… …=(u’v-v’u)/v² ...Применение производной в различных областях науки
Первый корпус БелГУ. с. Ливенка 2012год. Урок – деловая игра по теме: «Применение производной в различных областях науки». Корнева Г.Н., учитель математики, ...Применение производной
Дифференциальное исчисление создано Ньютоном и Лейбницем сравнительно недавно, в конце 17 столетия. Тем более поразительно, что за долго до этого ...Виды многогранников
Многогранником называется тело, ограниченное конечным числом плоскостей. Поверхность многогранника состоит из конечного числа многоугольников, которые ...Применение Формулы Пика
Георг Пик. Формула Пика была открыта австрийским математиком Георгом Пиком в 1899г. Краткая Биография. Георг Алекса́ндр Пик (10 августа 1859 — 13 ...Применение свойств функций к решению уравнений и неравенств
Содержание.Метод мажорант (метод оценки) Использование свойств функций: Область определения Множество значений Четность и нечетность 3. Задачи с ...
Логарифмы. Применение логарифмов
повторить определение логарифма; закрепить основные свойства логарифмов; - способствовать формированию умения применять свойства логарифмов при упрощении ...Каскады многогранников
Куб и тетраэдр. Тетраэдр можно вписать в куб так, что вершинами тетраэдра будут некоторые вершины куба. Упражнение 1. Найдите ребро тетраэдра, вписанного ...Вклад философов-математиков в развитие теории многогранников
Математика: лабиринты открытий. Стереометрия как наука известна уже очень давно. Изысканиями в этой области занимались многие видные умы древности. ...Виды многогранников
Геометрия является самым могущественным средством для изощрения наших умственных способностей.Г.Галилей. Многогранником называется тело, ограниченное ...
Применение теоремы Пифагора и пифагоровых троек для решения геометрических задач
Объект исследования: Теорема Пифагора и пифагоровы тройки. Предмет исследования: Применение пифагоровых троек для быстрого решения геометрических ...Модели многогранников
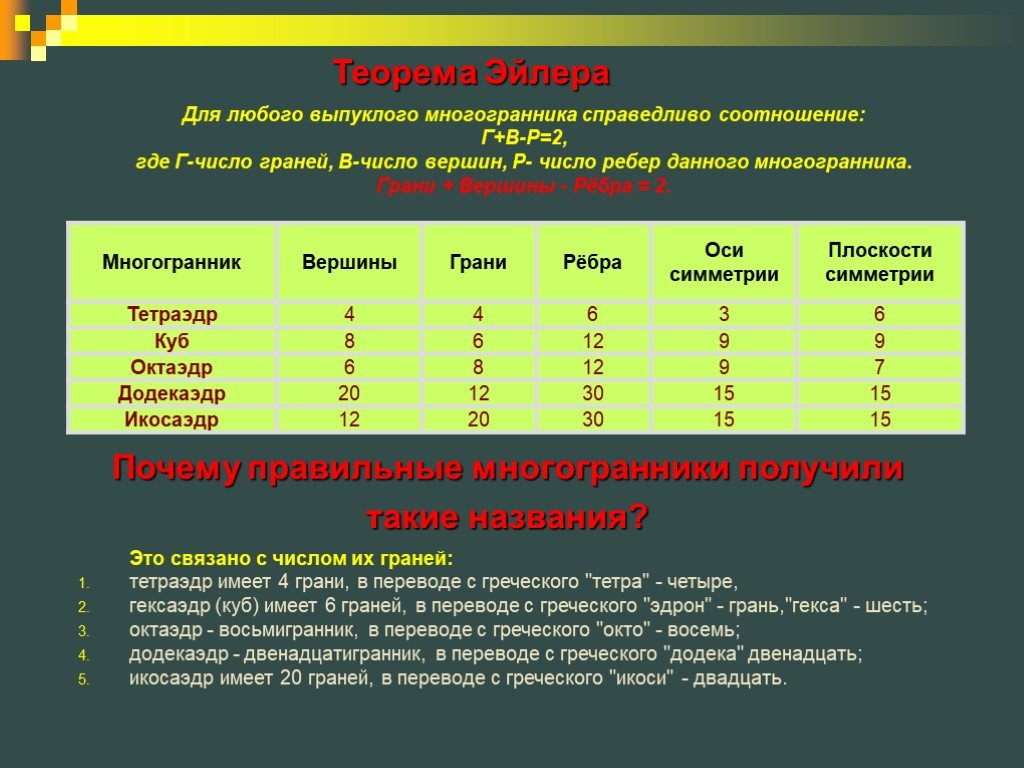
Правильным многогранником называется многогранник, у которого все грани правильные равные многоугольники, и все двугранные углы равны. Существует ...Сечение многогранников
Определения:. Секущая плоскость - плоскость, по обе стороны от которой имеются точки данного многогранника. Многоугольник – сторонами которого являются ...Конспекты
Применение формул сокращенного умножения
Конспект урока алгебры в 8 классе. Тема. : «Применение формул сокращенного умножения». . Тип урока:. урок обобщения и систематизации знаний. ...Применение свойств арифметического квадратного корня
Урок математики по теме: "Применение свойств арифметического квадратного корня" (8-й класс). . Аксютченко. . Жанна Владимировна,. учитель математики. ...Применение свойств рациональных чисел для рационализации вычислений
Тема: Применение свойств рациональных чисел для рационализации вычислений. Тип урока:. Формирование умений и навыков. Цели урока:. Обучающие:. ...Применение различных способов разложения на множители
Логинова Марина Николаевна. учитель математики. МКОУ Василёвская основная общеобразовательная школа. . Гусь-Хрустального района. ...Применение распределительного свойства умножения
Урок разработала:. Газеева Галина Вениаминовна. Класс:. 6. Предмет:. математика. Место проведения. : кабинет математики. Учебник: . «Математика, ...Применение производной к исследованию функции
МОУ Греково-Степановская СОШ. . Чертковского района Ростовской области. Учитель математики и информатики. Киселева Лариса Анатольевна. Урок алгебры ...Применение производной к исследованию функций. Наибольшее и наименьшее значение функции
ГОУ «Школа здоровья и индивидуального развития». Красногвардейского района. Санкт-Петербурга. Урок алгебры и начал анализа. ...Построение сечений многогранников
Государственное бюджетное образовательное учреждение. Лицей №281. «Построение сечений многогранников». Урок геометрии. 10 класс. ...Построение сечений многогранников на основе аксиоматики
Чудаева Елена Владимировна, учитель математики,. МОУ «Инсарская средняя общеобразовательная школа №1»,. г. Инсар, Республика Мордовия. . Автор. ...Построение правильных многоугольников
Открытый урок по геометрии в 9 классе(в рамках ФГОС). Учитель 1 кв. категории - Савченко Мария Анатольевна. МАОУ «Молчановская СОШ № 2» Молчановского ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:29 октября 2018
Категория:Математика
Содержит:19 слайд(ов)
Поделись с друзьями:
Скачать презентацию