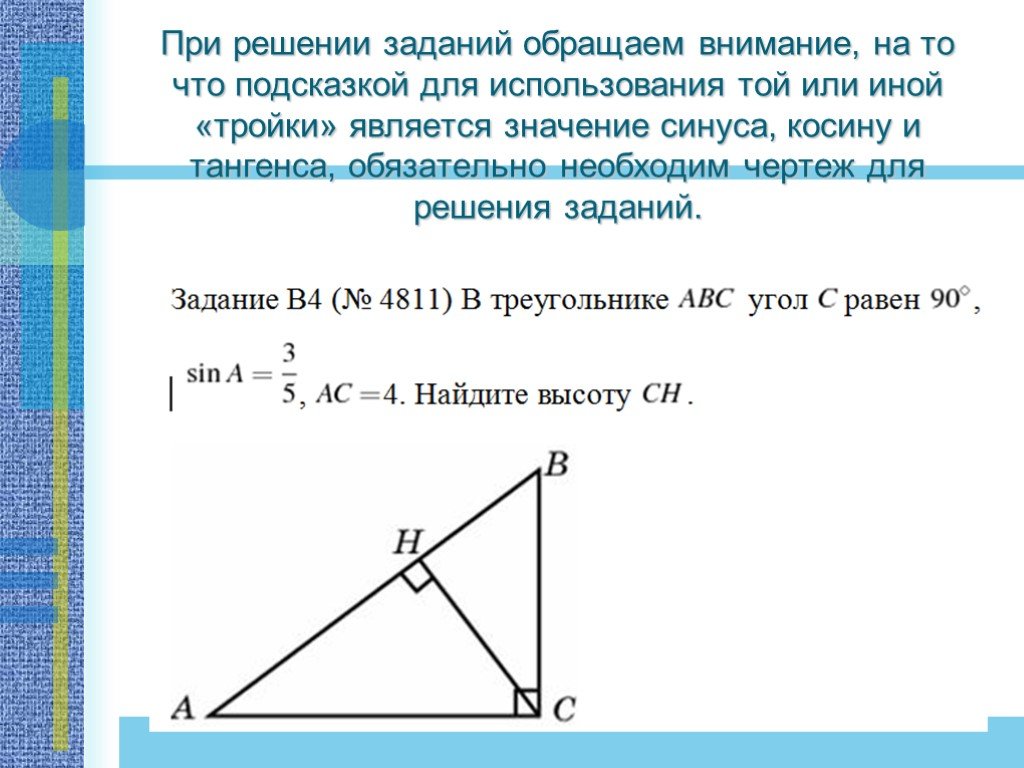
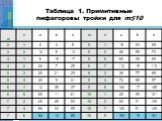
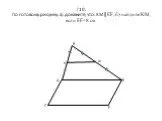
Презентация "Применение теоремы Пифагора и пифагоровых троек для решения геометрических задач" по математике – проект, доклад
Презентацию на тему "Применение теоремы Пифагора и пифагоровых троек для решения геометрических задач" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 24 слайд(ов).
Слайды презентации
Список похожих презентаций
«Применение производной для исследования функции»
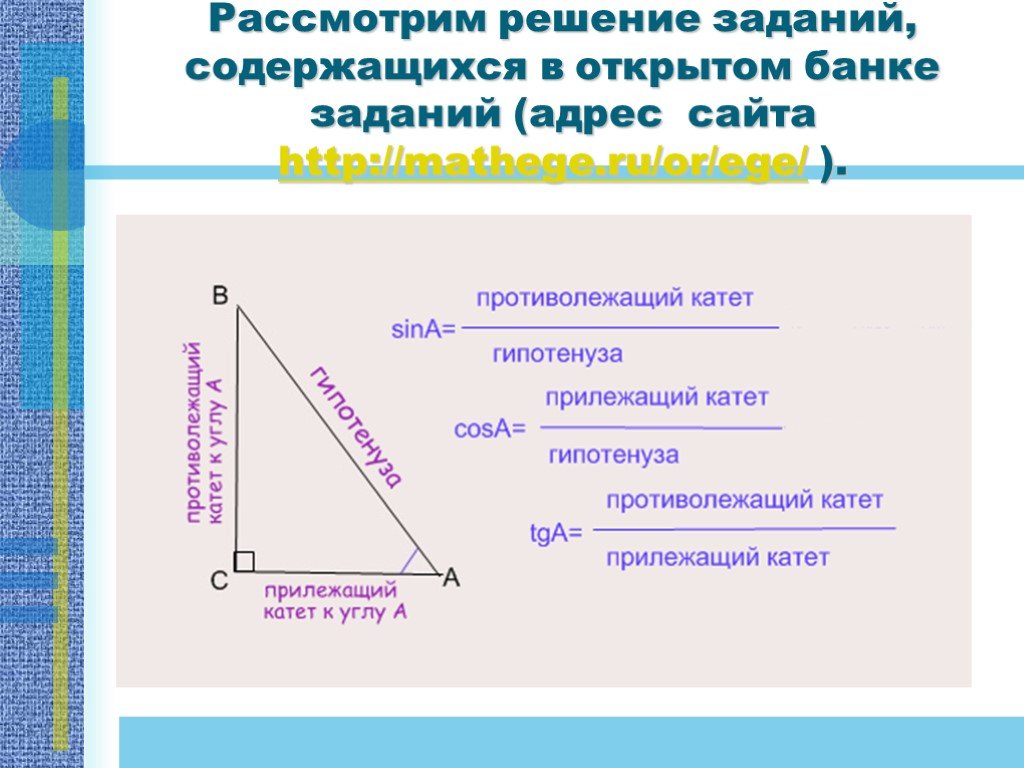
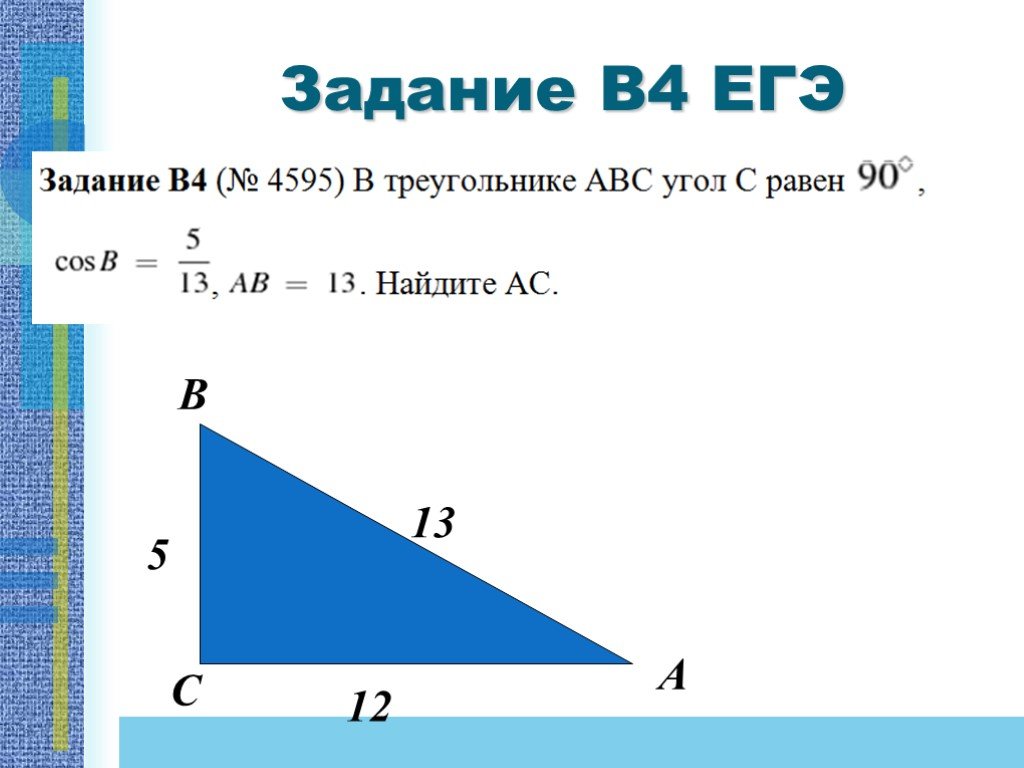
Справимся легко! №1. По графику функции y=f(x) ответьте на вопросы: Сколько точек максимума имеет эта функция? Назовите точки минимума функции. Сколько ...Cпособы доказательства теоремы Пифагора
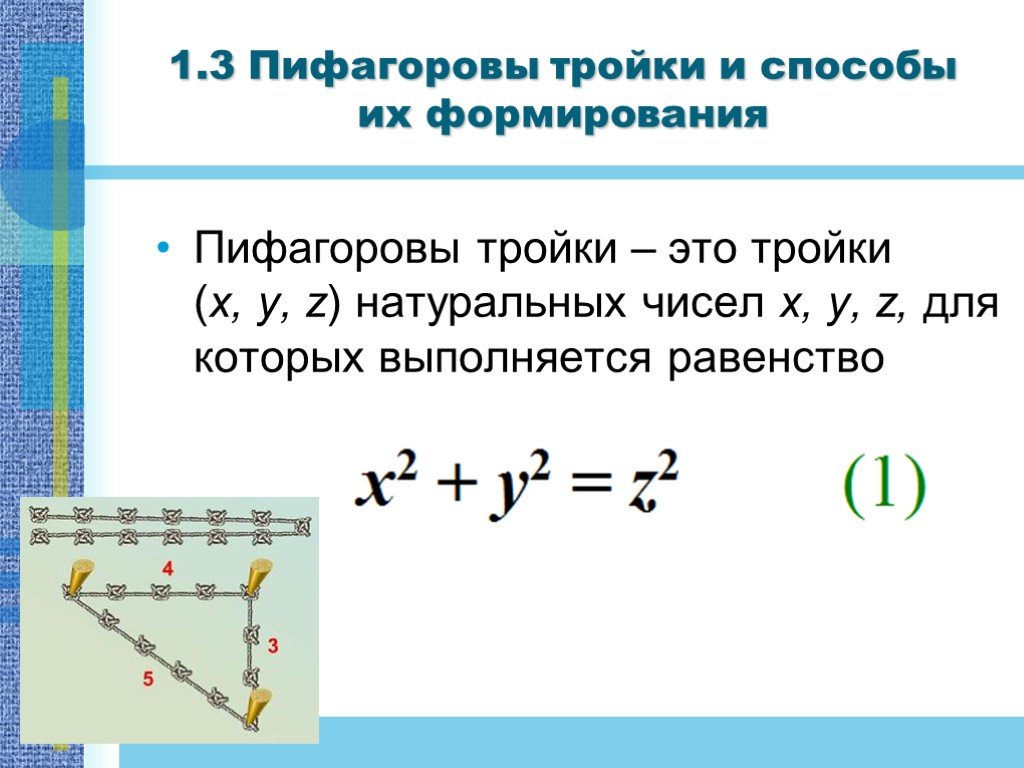
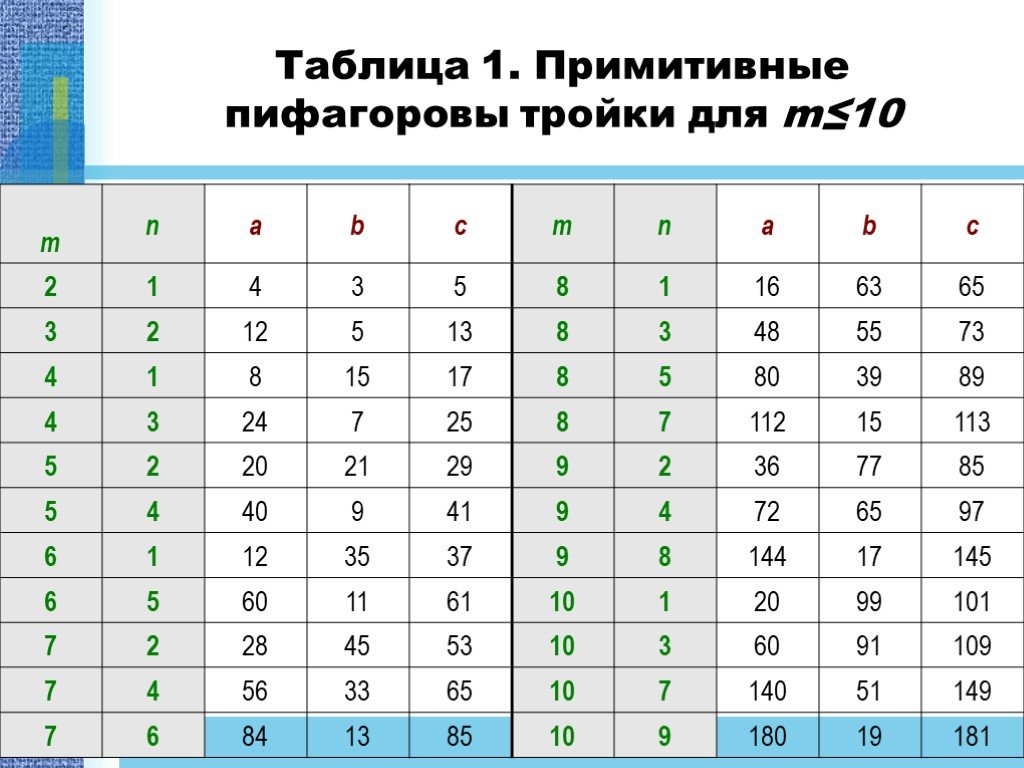
a2+b2=c2 c a b П. Пифагор не открыл это свойство прямоугольного треугольника, он, вероятно, первым сумел его обобщить и доказать, перевести тем самым ..."Разрезание геометрических фигур на части"
ЗАДАЧИ НА РАЗРЕЗАНИЯ. Теорема Бойяи-Гервина гласит: любой многоугольник можно так разрезать на части, что из этих частей удастся сложить квадрат. ...«Решение задач с помощью пропорций»
Найти значение Х: Х:3=4:6 5:Х=2:6 7:3=Х:18 Устная работа. Указать вид пропорциональной зависимости:. Какова зависимость пути от времени? Какова зависимость ...Алггоритм. Решение задач
Задача 1. В урне хранится некоторое количество чёрных и белых шаров. Требуется разложить эти шары по двум корзинам чёрного и белого цвета: белые шары ...«Решение задач по математике»
10 февраля. В классе. Задача условие вопрос решение ответ. Быстро и правильно считать. Правильно записывать решение задачи. Кричать и сердиться, когда ...Автоматизация труда учителя на примере решения систем алгебраических уравнений с использованием программного пакета MATHCAD
Ознакомить учителей математики с возможностями продукта MathCAD Обеспечить автоматизацию работы учителей с использованием MathCAD Рассмотреть решение ...Авторские задачи по математике и физике, составленные по повести Н.В. Гоголя «Ночь перед Рождеством
Методологическая основа: Класс арифметических задач огромен. Учащиеся старших классов обычно пытаются решать такие задачи алгебраически, так как владеют ...Аксиомы стереометрии Решение задач
Через любые две точки пространства проходит единственная прямая. Через любые три точки пространства, не принадлежащие одной прямой, проходит единственная ...7 способов решения тригонометрического уравнения
Математики видят ее в:. гармонии чисел и форм, геометрической выразительности, стройности математических формул, решении задач различными способами, ...Аксиомы стереометрии и их следствия. Решение задач
Цель урока: обобщение и применение аксиом и их следствий к решению задач. Математический диктант. 1). Сформулируйте аксиомы стереометрии: Аксиома ...10 способов решения квадратных уравнений
История развития квадратных уравнений. Квадратные уравнения в Древнем Вавилоне: Х2+Х=3/4 Х2-Х=14,5. Как составлял и решал Диофант квадратные уравнения. ...«Треугольники и их виды»
Геометрические фигуры. а ж е д с б и з. Треугольники и их виды. Определение треугольника, элементы треугольника Виды треугольников Сумма углов треугольника ..."Турнир веселых и смекалистых знатоков истории, физики, химии, математики"
Цели мероприятия: 1.Развитие у учащихся интереса к изучаемым предметам. 2.Показать необходимость знаний по математике в других науках. 3.Формирование ...Активные и Смелые, Артисты и Спортсмены, Аккуратные и Старательные, Артистичные и Симпатичные, Одним словом, наш класс- ПЯТЫЙ АС!
Наш класс весёлый и смешной, Красивый он и смелый. Там есть артисты и певцы, Танцоры и спортсмены. И там улыбка каждый день, И солнце в окна светит, ..."Число и цифра 9"
Число и цифра 9. Тема урока:. Цель урока:. познакомить с числом 9, обучить написанию цифры 9. Задачи урока:. вспомнить времена года, дни недели, месяцы; ..."Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке
1. Найти наибольшее значение функции по её графику на [ -5;6] и [-7; 6]. 5 4 -5 у наиб. = 4 [-5; 6] у наиб. = 5 [-7; 6] 1. 2. Найти наименьшее значение ..."Сложение и вычитание рациональных чисел"
I. II. III. IV. Тема: "Сложение и вычитание положительных и отрицательных чисел". Станции: Историческая Биологическая Географическая Математическая. ...«Правильные и неправильные дроби»
«Учёные Грузии нашли золото в составе крови человека». Из журнальной статьи. “ЗОЛОТАЯ КРОВЬ” (ЭДУАРД АСАДОВ). Не так давно учёные открыли Пусть небольшой, ...«Параллельность прямых и плоскостей»
ABCD – трапеция, AD , E и F – середины AB и CD соответственно. Докажите, что EF ǁ α. α. α. α. α. A B C D α. Через вершины А и С параллелограмма ABCD ...Конспекты
Алгоритм решения задачи на нахождение целого и частей
. Тимошенкова. Ирина Викторовна. Учитель начальных классов. МБ НОУ «Гимназия № 70». Г. Новокузнецк. Алгоритм. решения задачи. ...Web -разработка. Применение производной.10 класс
ТЕХНОЛОГИЧЕСКАЯ КАРТА КОНСТРУИРОВАНИЯ УРОКА С ИСПОЛЬЗОВАНИЕ СРЕДСТВ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ. Учитель Беломестнова Наталья Петровна. Предмет, ...Бинарный урок математики и кубановедения. Проценты
Бинарный урок математики и кубановедения. Проценты. Цель урока:. воспитательные:. - активизация познавательной и творческой деятельности учащихся;. ...Белоснежка и семь гномов
Муниципальное автономное дошкольное общеобразовательное учреждение. «Детский сад комбинированного вида» №221. Кемеровской области. Конспект ...Арифметический корень натуральной степени и его свойства
Урок алгебры в 9 классе. . Тема урока. : «Арифметический корень натуральной степени и его свойства». . Из опыта работы учителя математики. ...Арифметический квадратный корень и его свойства
Тема: «Арифметический квадратный корень и его свойства». Урок-игра «Аукцион математических знаний». Цели урока. :. . Образовательные:. - ...+ двухзначных и однозначных чисел в пределах 100
УРОК МАТЕМАТИКИ. Тема:. + двухзначных и однозначных чисел в пределах 100 (урок обобщения). Цель:. Создание условий для формирования УУД при ...Верные и неверные равенства и неравенства
Муниципальное бюджетное образовательное учреждение. средняя общеобразовательная школа №1. . города Ярцева Смоленской области. . Конспект ...Величины (длина, масса, время, объем) и единицы измерения
Математика 3-1-8. . Тема урока. :. Величины (длина, масса, время, объем) и единицы. . измерения. Цели:. повторить единицы измерения массы, ...Алгоритм и его формальное исполнение
Тема урока: «. Алгоритм и его формальное исполнение. ». Цели:. усвоить что такое алгоритм и каковы его свойства;. . научиться составлять ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 апреля 2019
Категория:Математика
Содержит:24 слайд(ов)
Поделись с друзьями:
Скачать презентацию