Конспект урока «Применение производной к исследованию функции» по алгебре

МОУ Греково-Степановская СОШ

Чертковского района Ростовской области

Учитель математики и информатики

Киселева Лариса Анатольевна

Урок алгебры в 11 классе

Урок – смотр знаний

Тема урока

Применение производной к исследованию функции

Цели урока:

Дидактическая:

обеспечить проверку теоретических знаний и умений по теме «Применение производной к исследованию функции».

Развивающая:

развитие умений применять знания в конкретной ситуации; развитие логического мышления; умений сравнивать, обобщать, правильно излагать мысли; развитие самостоятельной деятельности учащихся.

Воспитательная:

воспитание интереса и любви к предмету через содержание учебного материала, умения работать в коллективе, взаимопомощи, культуры общения; воспитание таких качеств характера, как настойчивость в достижении цели; умение не растеряться в проблемных ситуациях.

План проведения урока:

1. Организационный момент.

2. Актуализация знаний учащихся.

3. Работа в группах по карточкам.

4. Историческая справка.

5. Домашнее задание.

6. Итог урока.

Ход урока

1. Организационный момент.

• Приветствие.

• Сообщение цели урока.

• Объявление плана урока.

2. Актуализация знаний учащихся.

1. Учащиеся поднимают руку, если согласны с утверждением, и не поднимают – если не согласны.

• В точке возрастания функции её производная больше нуля. (Верно).

• Если производная функции в некоторой точке равна нулю, то в этой точке имеется экстремум! (Неверно).

• Производная произведения равна произведению производных. (Неверно).

• Наибольшее и наименьшее значения функции на некотором отрезке наблюдаются или в стационарных точках, или на концах отрезка. (Верно).

• Любая точка экстремума является критической точкой. (Верно).

2. На экране по очереди появляются слайды с чертежами и заданиями к ним. Учащиеся фиксируют в тетрадях ответ. Затем на экран выводятся правильные ответы. Самопроверка.

1 слайд

1 задание: Функция y = f(x) определена на промежутке (- 6; 6). На рисунке изображён график её производной. Найдите точки, в которых производная функции равна нулю.

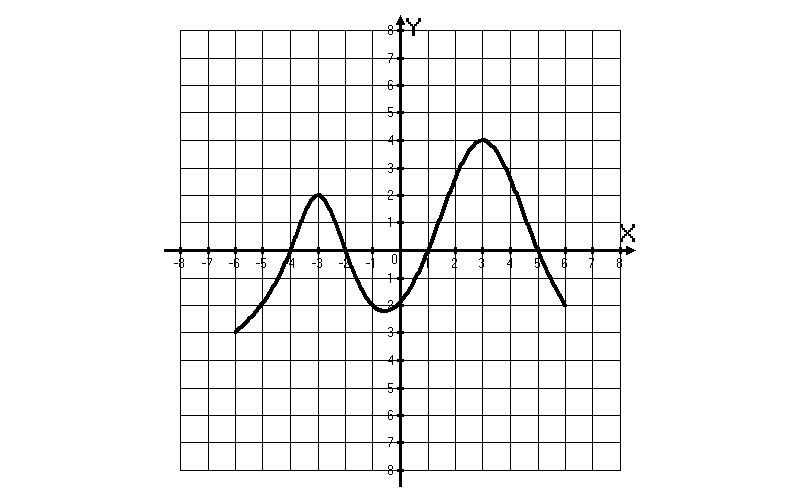
2 слайд

2 задание: Функция y = f(x) определена на промежутке (-6; 5). На рисунке изображён график её производной. Укажите количество промежутков, на которых функция возрастает.

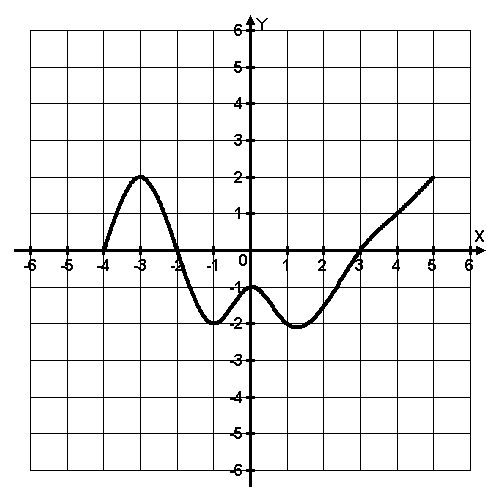
3 слайд

3 задание: Функция y = f(x) определена на промежутке (-4; 5). На рисунке изображён график её производной. Найдите точку минимума функции y = f(x).

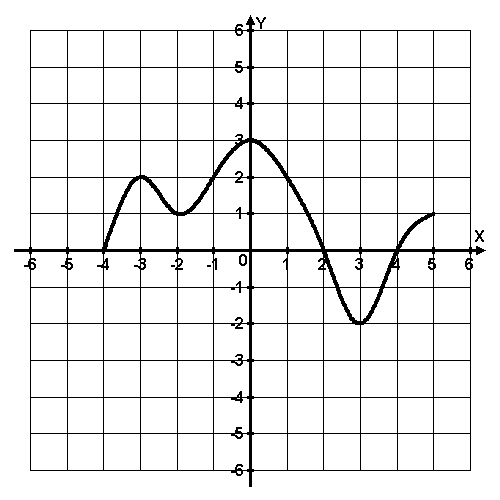
4 слайд

4 задание: Функция y = f(x) определена на промежутке (-4; 5). На рисунке изображён график её производной. Найдите точку максимума функции y = f(x).

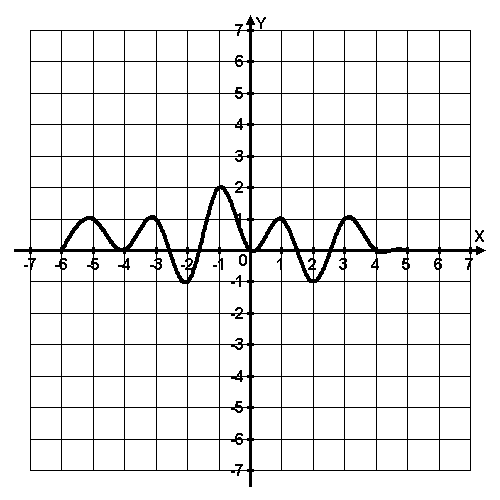
5 слайд

5 задание: Функция y = f(x) определена на промежутке (-5; 5). На рисунке изображён график её производной. Укажите точку, в которой функция принимает наименьшее значение.

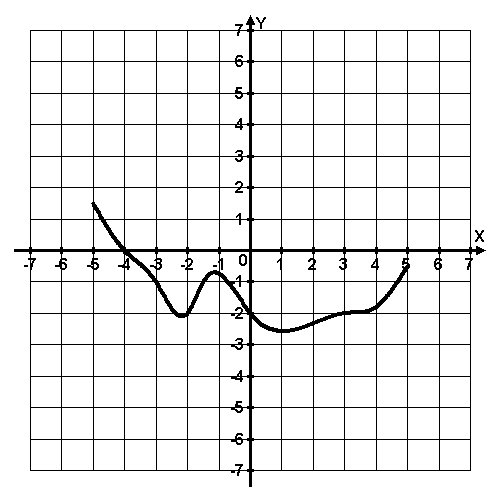
6 слайд

Ответы: 1 задание: х = - 4; х = - 2; х = 1; х = 5

2 задание: 5

3 задание: х = 3

4 задание: х = 2

5 задание: х = - 4

3. Работа в группах по карточкам.

Учащиеся делятся на 3 группы. Каждая группа получает карточку. Через некоторое время каждая группа по очереди отвечает у доски.

Карточка № 1.

1. Расскажите достаточные признаки возрастания и убывания функции.

2. Исследуйте функцию и постройте её график f(x) = 1/3х³ – 3х

3. Найдите наибольшее и наименьшее значения функции f(x) = - x³ + 2x² -8х + 1 на отрезке [- 2; 1].

Карточка № 2.

1. Расскажите о применении производной к нахождению критических точек, её максимумов и минимумов.

2. Найдите наибольшее и наименьшее значения функции f(x) = 1/3x³ – 9х + 10 на отрезке [0; 6].

3. Исследуйте функцию и постройте её график f(x) = x⁴ – 8x².

Карточка № 3.

1. Расскажите план нахождения наибольшего и наименьшего значения функции на отрезке.

2. Найдите промежутки возрастания и убывания функции

f(x) = 0,2х⁵ – х³ – 4х + 1

3. Исследуйте функцию и постройте её график f(x) = 6х – 2х³ + 1

4. Историческая справка.

Производная - одно из фундаментальных понятий математики. Оно возникло в XXVII веке в связи с необходимостью решения ряда задач из физики, механики и математики, но в первую очередь следующих двух: определение скорости прямолинейного движения и построения касательной к прямой. Независимо друг от друга И. Ньютон и Г. Лейбниц разработали аппарат, которым мы и пользуемся в настоящее время. И. Ньютон в основном опирался на физическое представление о мгновенной скорости движения, считая его очевидным и сводя к нему другие случаи производной, а Г. Лейбниц использовал понятие бесконечно малой. Исчисление созданное Ньютоном и Лейбницем, получило название дифференциального исчисления. С его помощью был решен целый ряд задач теоретической механики, физики и астрономии. В частности, используя методы дифференциального исчисления, ученые предсказали возвращение кометы Галлея, что было большим триумфом науки XVIII в. С помощью тех же методов математики изучали в XVII и XVIII вв. различные кривые, нашли кривую, по которой быстрее всего падает дифференциального исчисления сыграл Л. Эйлер, написавший учебник «Дифференциальное исчисление».

Основные понятия дифференциального исчисления долгое время не были должным образом обоснованы. Однако в начале XIX в. французский математик О. Коши дал строгое построение дифференциального исчисления на основе понятия предела.

Применяемая сейчас система обозначений для производной восходит к Лейбницу и Лагранжу.

В настоящее время понятие производной находит большое применение в различных областях науки и техники.

5. Домашнее задание: (дифференцировано по уровню сложности).

1. «Проверь себя!»

2. № 968; № 970 (1); № 973

6. Итог урока.

ИСТОЧНИКИ МАТЕРИАЛОВ

1. Глейзер Г.И. История математики в школе. IX—X кл.  М.: Просвещение, 1983.

2. Григорьева Г.И. Алгебра: 11 класс: Ч. 1, 2: Поурочные планы по учебнику Ш.А.Алимова, Ю.М.Колягина, Ю.В.Сидорова. М.: Просвящение. 2002

3. ЕГЭ -2011. Математика. Типовые экзаменационные варианты: 30 вариантов. Под ред. Семенова А.Л., Ященко И.В. М.: Национальное образование, 2010

4. Максимовская М. А. Тесты по математике 5 – 11 классы. М: Олимп. 2003

5. Математика. Подготовка к ЕГЭ- 2011.  Под ред. Лысенко Ф.Ф., Кулабухова С.Ю. Ростов-на-Дону: Легион-М, 2010

6. Ткачева М.В. Федорова Н.Е. Шабунин М.И. Алгебра и начала анализа: Дидактические материалы для 10-11 классов. М.: Мнемозина. 2001

7. http://www.neuch.ru/referat/41434.html

8. http://studyport.ru/tochnyie-nauki/ekstremumyi-funktsiy