Конспект урока «Производная. Физический и геометрический смыл производной» по алгебре для 11 класса

Тема «Производная. Физический и геометрический смыл производной»

Тип урока – обобщающий.

Вид – комбинированный.

Цели урока:

• Обучающие:

повторить основные формулы и правила дифференцирования, физический и геометрический смысл производной; сформировать умение комплексного применения знаний, умений, навыков и их перенос в новые условия; проверить знания, умения, навыки учащихся по данной теме.

• Воспитательные: Воспитывать интерес к предмету.

• Развивающие: содействовать развитию мыслительных операций: анализ, синтез, обобщение; формированию умений самооценки и взаимооценки, познавательную активность, развивать вычислительные навыки.

Оборудование:

• Мультимедийный проектор.

• Мультимедийная доска.

• Компьютер.

• Презентация с заданиями.

• Приложения с основными формулами и правилами дифференцирования .

• Карточки для проведения рефлексии, оценочные листы

1. Организационный момент.

Приветствие класса. Проверка готовности класса к уроку.

2. Сообщение темы и целей урока.

3. Теоретический опрос.

• Сформулируйте определение производной.

• Как называется операция нахождения производной?

• Какая функция называется дифференцируемой в точке?

• В чем заключается физический смысл производной?

• В чем заключается геометрический смысл производной?

• Какая функция называется дифференцируемой на некотором промежутке?

• Сформулируйте правило нахождения производной суммы, произведения, частного.

Параллельно один из учащихся работает с формулами на мультимедийной доске. Работа проходит в виде игры в лото «Собери формулы» Например:

(a^x)’

.

4. «Верно- неверно».

Каждому учащемуся раздаются карточки белого и черного цветов. Если ученик согласен с ответом -он поднимает белую карточку, если - нет – черную. Цель данного задания – понимание смысла теоретических знаний.

• Верно ли, что тангенс угла наклона касательной к графику функции– это есть значение производной в точке касания?

да

• Верно ли, что функция дифференцируема на отрезке [a,b], если она имеет производную в каждой точке интервала (а,b)?

нет

• Верно ли, что производная суммы функций равна сумме производных функций?

да

• Верно ли, что производная функции у = ln x имеет производную в точке х = - 5?

нет

• Верно ли , что первая производная пути от времени – это есть ускорение материальной точки?

нет

• Верно ли, что функция у =cos x дифференцируема на множестве действительных чисел?

да

• Верно ли, ( f(x)·g(x))’=f’(x)·g’(x)?

нет

5. Устный счёт. Задачи с выбором ответов .

У каждого учащегося на столе лежат карточки с номерами 1, 2, 3. Учащиеся поднимают номер правильного ответа.

1.

Найти у’, если у = ln(3x-1)

2

Найти у’, если у = (2х+1)²

1. 2. 3.

3.

1. 4(2х+1) 2. 2(2х+1) 3. 4х

4. Найти мгновенную скорость точки, если закон её движения выражается формулой s(t) =

1. 2. 3.

5. Вычислить угловой коэффициент касательной в точке х=4 к графику функции

1. 2. 3. 2

Работа у доски.

1. Найти значение производной функции у(х) в заданной точке х ₀

• у = ln(x+1)-e^x+3sin3x+log₃Х X₀ =0

• y = 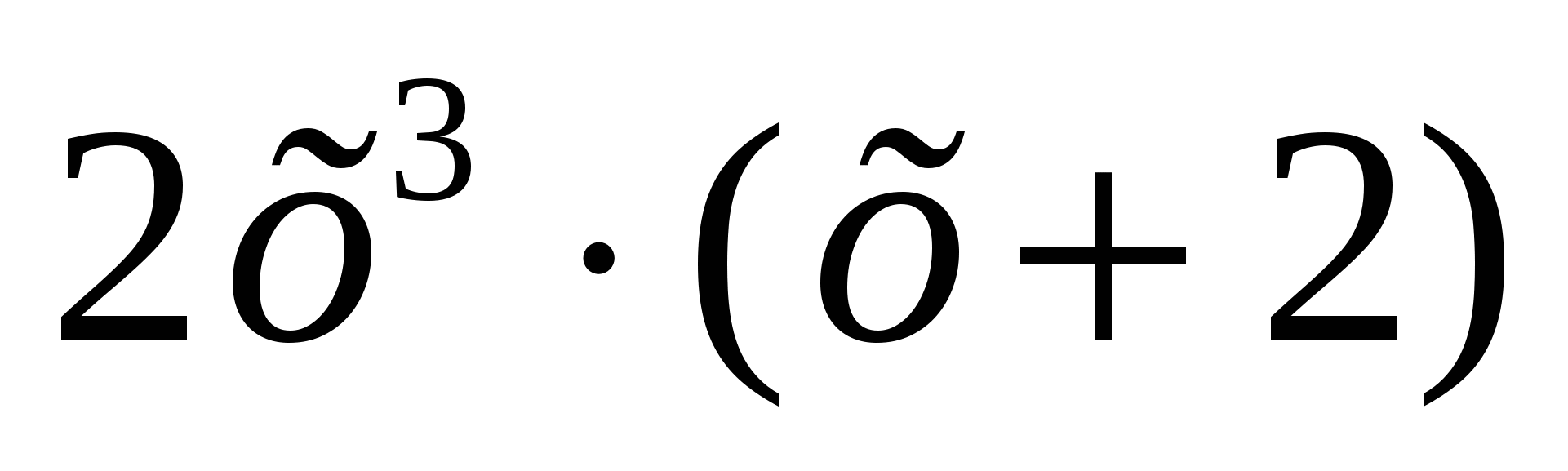- 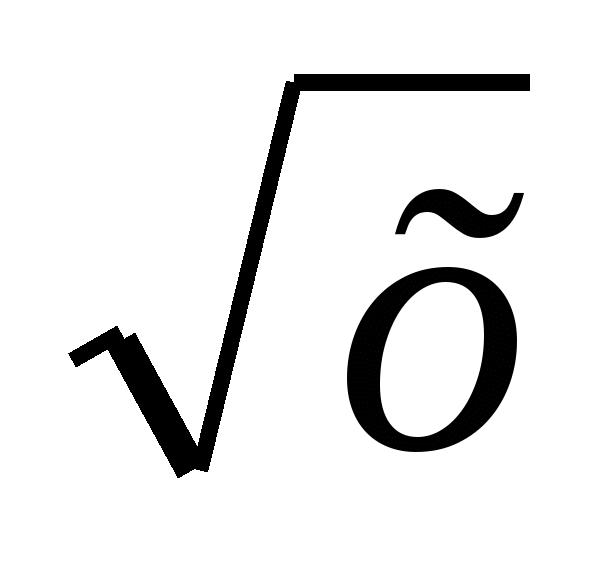X₀ =1

• y = 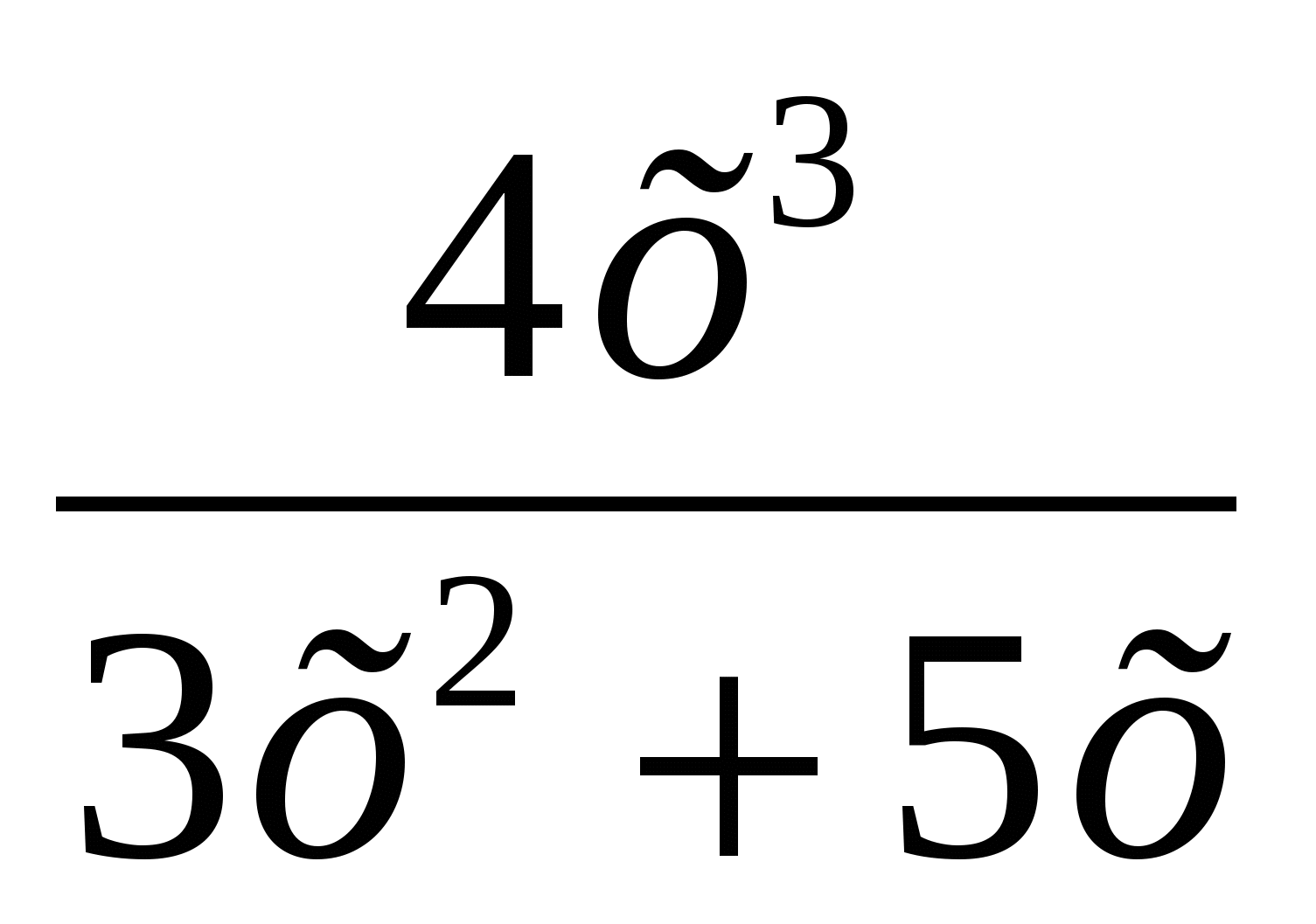+ lnx X₀ =1

2. При движении тела по прямой расстояние S (в метрах ) от начальной точки изменяется по закону s(t) = (t – время движения в секундах). Через сколько секунд после начала движения тело сделает вторую мгновенную остановку, если V_мгн = 0.

3. Найти тангенс угла наклона касательной к графику функции у = 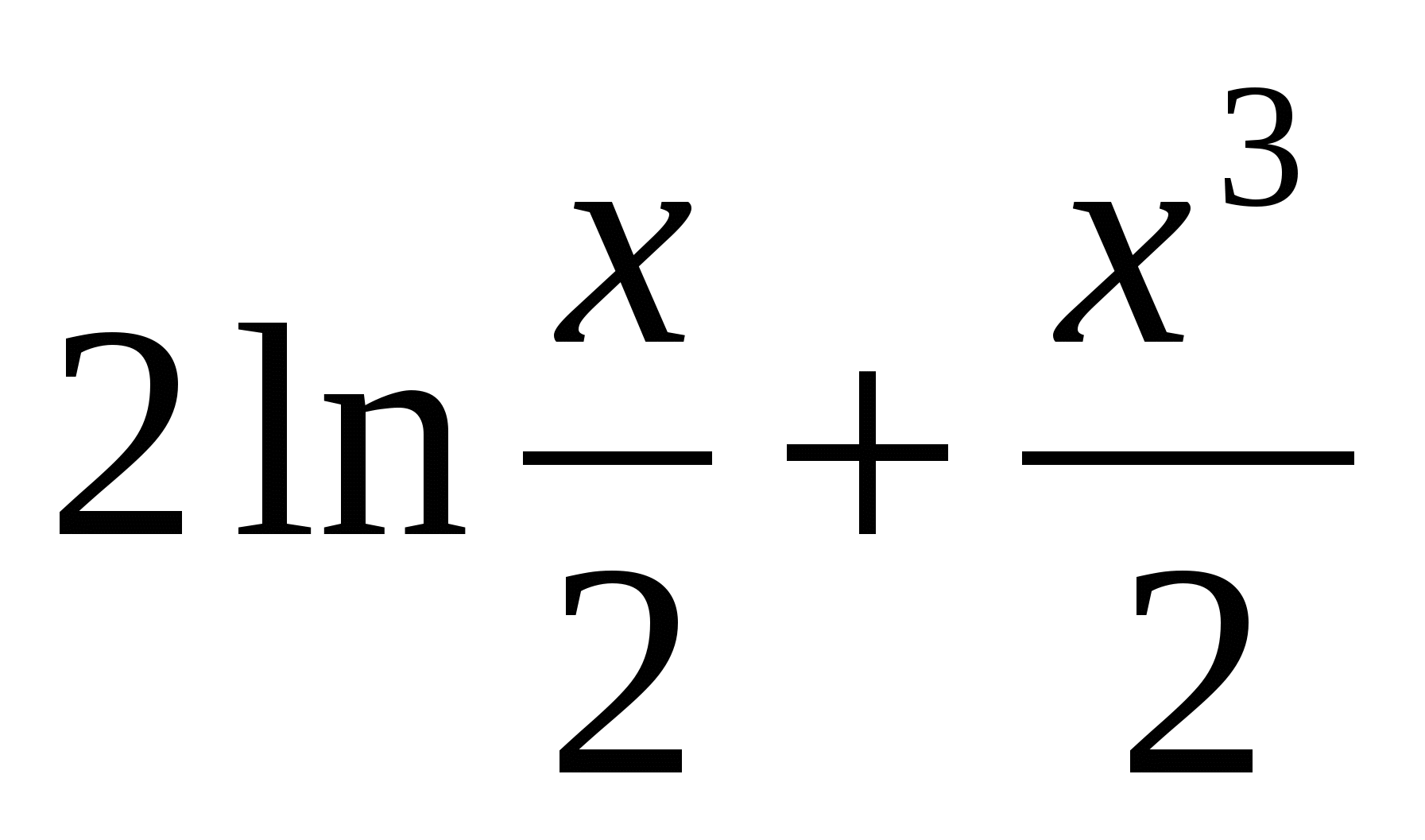в точке с абсциссой .

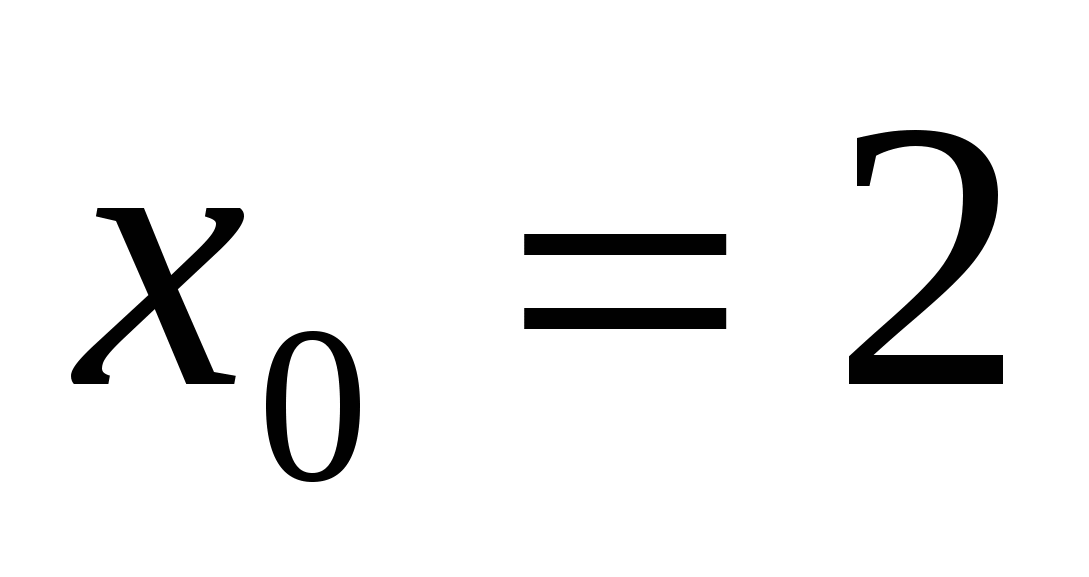Самостоятельная работа.

I вариант

1. При движении тела по прямой расстояние S (в метрах ) от начальной точки изменяется по закону s(t) = 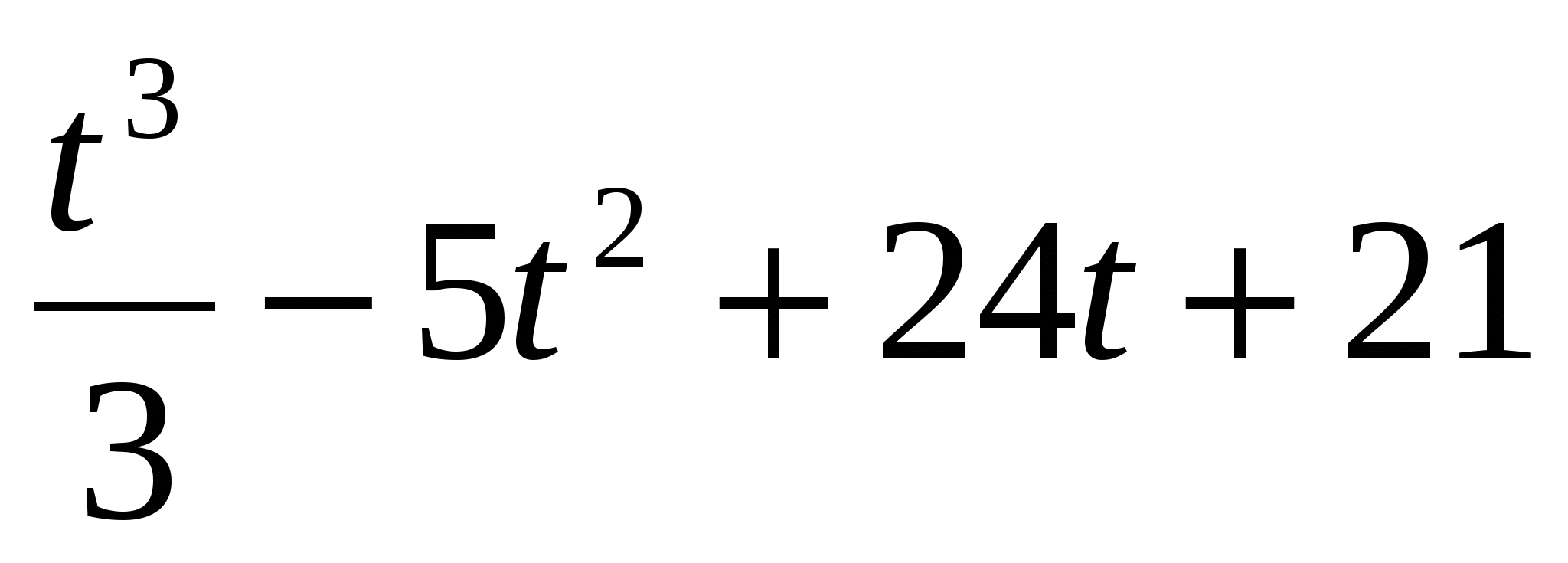(t – время движения в секундах). Сколько мгновенных остановок сделает тело за первые 5 сек. своего движения, если V_мгн = 0.

2. Вычислить производную функции у =

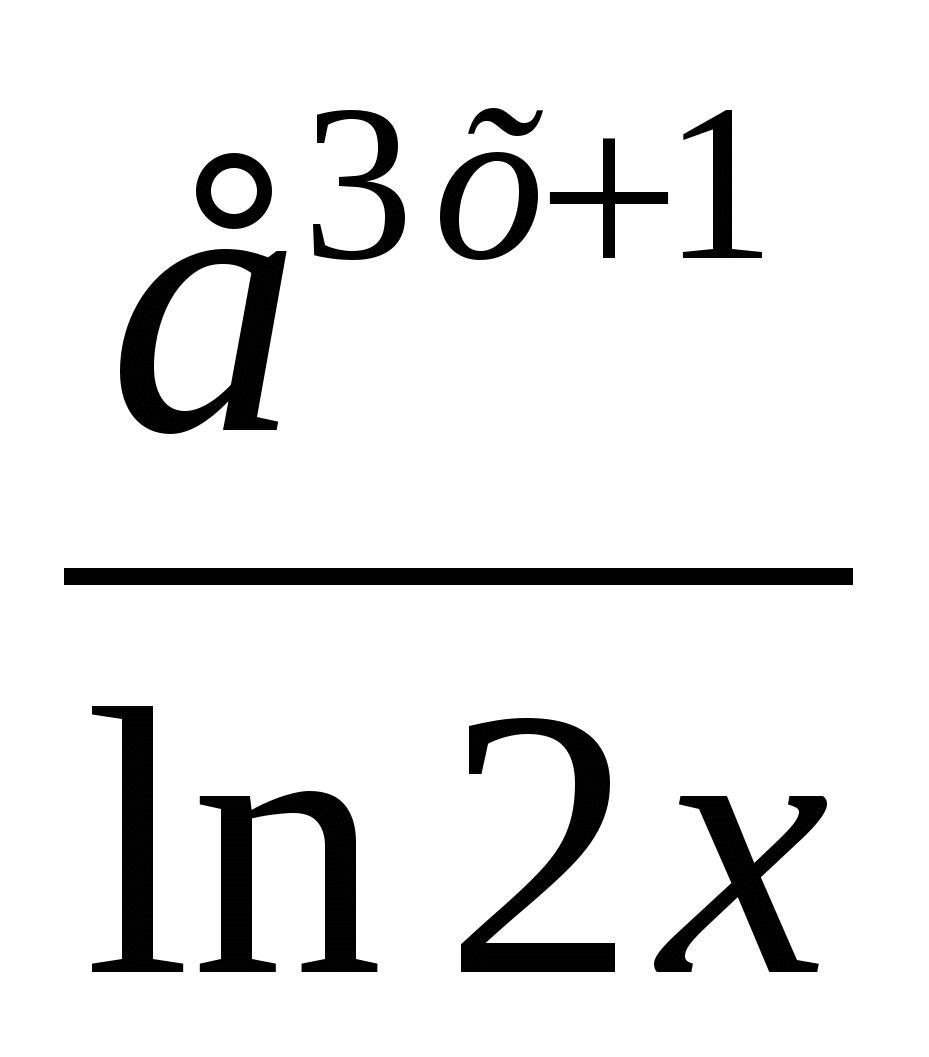
II вариант.

1. Через точку графика функции у = 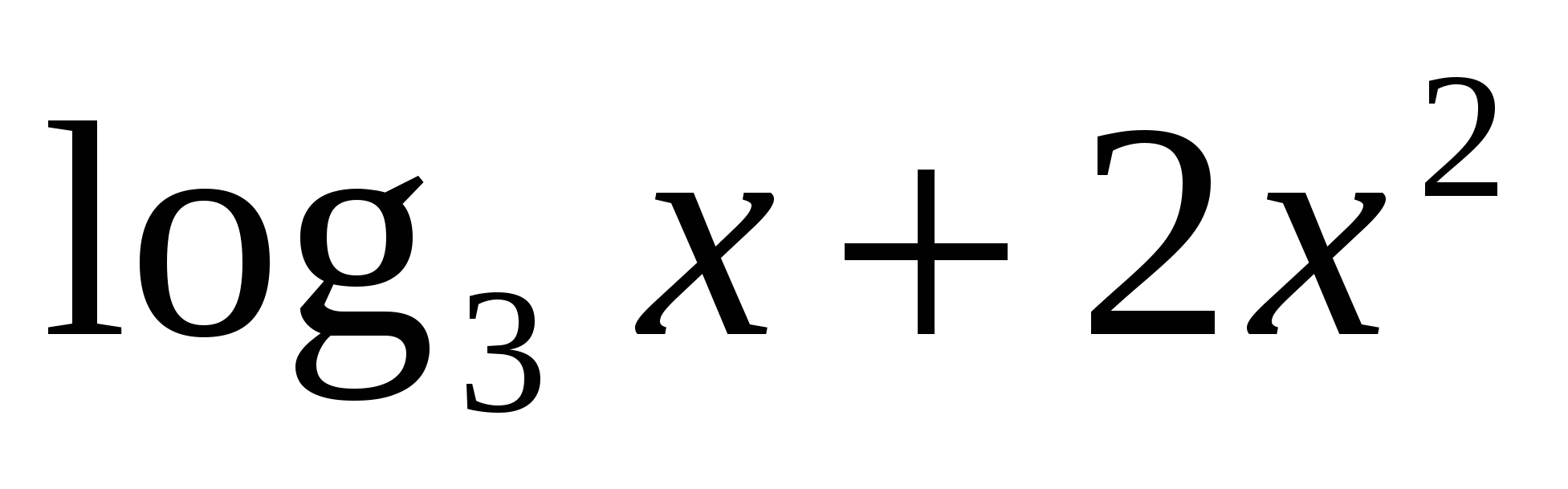с абсциссой 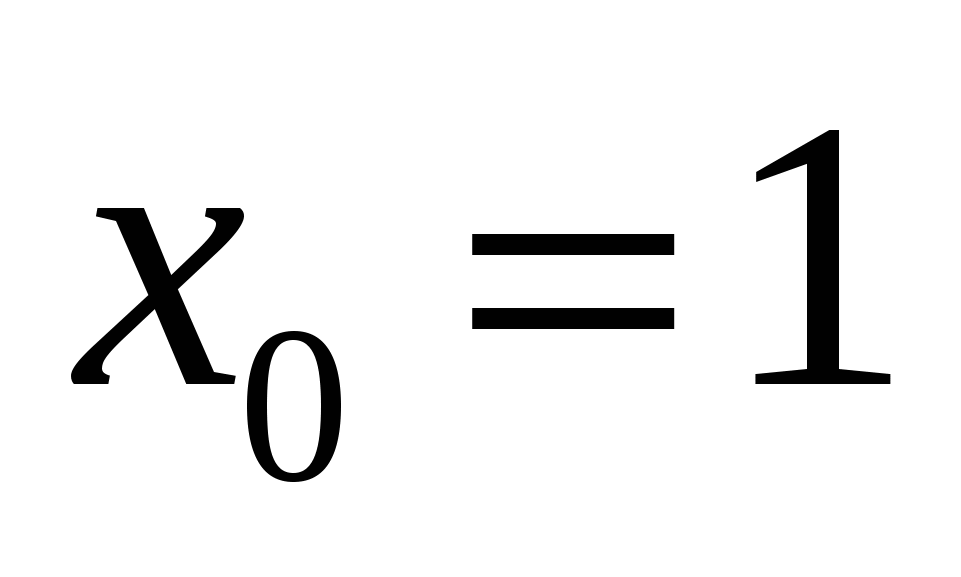проведена касательная. Найдите её угловой коэффициент.

2. Вычислить производную функции у = cos(8-4x)· .

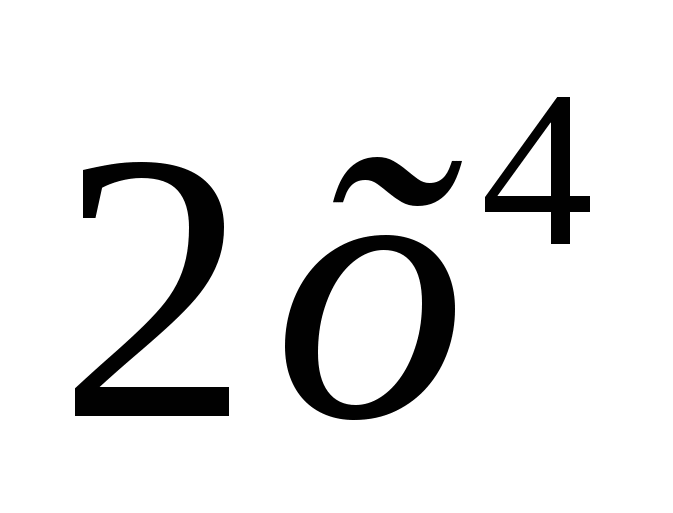Итог урока.

Учащимся предлагается ответить на следующие вопросы:

Сегодня на уроке:

Я повторил …………..

Я закрепил умения вычислять………………..

Теперь я знаю ………………………

Оценивание учащихся по учетным карточкам.

Домашнее задание.

Проверь себя стр. 254

Фамилия Имя. Класс ____________________________________