Конспект урока «Геометрический смысл производной» по алгебре

Открытый урок по теме:

«Геометрический смысл производной».

Цели урока: дать понятие углового коэффициента прямой, определение угла между прямой и осью Ох; выяснить геометрический смысл производной, научить составлять уравнение касательной к графику функции и применять теоретические знания на практике.

Тип урока: комбинированный.

Оборудование: презентация по изучаемой теме, карточки-задания.

Ход урока:

1. Организационный момент (3 мин)

2. Сообщение темы урока, постановка его целей и задач, мотивация учебной деятельности ( 5 мин) (слайд №1)

Нам необходимо ответить на следующие вопросы:

1)Что называется секущей и касательной?

2)В чём заключается геометрический смысл производной функции в точке?

3)Какое уравнение имеет касательная к графику функции в точке?

Эпиграфом нашего урока будут следующие слова, которые принадлежат российскому учёному-математику: (слайд №2).

«Холодные числа, внешне сухие формулы математики полны внутренней красоты и жара сконцентрированной в них мысли»

3. Активизация познавательной деятельности, воспроизведение и коррекция опорных знаний (12 мин)

Закончите предложение (записывая подряд буквы правильных, по вашему мнению, слов, вы узнаете фамилию этого учёного) (слайд № 3 ):

1) Закон или правило, согласно которому каждому элементу х из одного множества ставится в соответствие единственный элемент у из другого множества.

2) Элемент х называется …

3. Элемент у называется…

Точка на координатной плоскости имеет два значения: х и у.

4) Значение х называется… .

5) Значение у называется… .

6) Функция, заданная формулой у = кх + b, где к, b- числа, х-переменная называется… .

7) Функция, заданная формулой у=ах²+bх+с, где а, b, с - числа, х - переменная называется… .

8) Функция, заданная формулой у=хᵖ, где р-любое число, х- переменная называется… .

9) Функция, заданная формулой у=аᵡ, где а˃0,а≠1, х-переменная называется… .

10) Функция, заданная формулой у=Ɩogₐх, где а˃0, а≠1, х˃0 называется… .

11) Функция, заданная формулой у=соsх, где х - переменная называется…

Слова для справок:

(К) Абсциссой

(Р) Показательной

(А) Функцией

(С) Ординатой

(О) Логарифмической

(Л) Аргументом

(В) Тригонометрической

(Е) Значением функции

(А) Линейной

(Д) Степенной

(Н) Квадратичной

4. Подготовка к восприятию нового материала. (10 мин.)

Решение многих задач приводит к понятию производной: это и определение мгновенной скорости и ускорения в данный момент времени, мощности, силы тока и напряжения переменного тока и т.д.

Сейчас мы остановимся на геометрической задаче - построение касательной к кривой. Сначала вспомним: (слайд №4)

1) как называется график линейной функции у = кх + b. (Прямая).

2) Как называется коэффициент к. (Угловым коэффициентом прямой)

α- угол между прямой и положительным направлением оси Ох.

3) Какая связь между к и α. (к = tgα)

4) Что называется тангенсом угла. (Это отношение абсциссы точки к её ординате)

Итак, если известен угол α, то можно определить число к. А, если дана точка на прямой, то и число b.

Пример 1. Найти значения k и b, если прямая у = кх + b проходит через точку (x₀; y₀) и образует с осью Ох угол α

α = π∕4, х₀=2, у₀=-3. Найти к и b. Решение: к = tg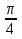 = 1, у₀ = кх₀ + b, b = у₀ - кх₀, b = -3-2=-5

Ответ: 1 и -5.

5. Изучение нового материала. (15 мин)

Если не дан угол α, то число к можно найти с помощью производной (слайд №5)

Рассмотрим график функции. Пусть точки А и М принадлежат графику этой функции. Прямая АМ называется секущей. Определим координаты точек А, М и С.

А(х, ƒ(х)), М(х+h, ƒ(х+h)), С(х+h, ƒ(х))

Рассмотрим ∆ АМС: tgα = МС: АС, где МС = ƒ(х+h) – ƒ(х), АС = h, т.е. к = tgα= ∆ƒ ∕ h

Пусть число х фиксировано,тогда точка А неподвижна, а точка М при h→0 двигаясь по графику, стремится к точке А. При этом прямая АМ стремится занять положение некоторой прямой, которую называют касательной к графику функции у=ƒ(х)

Угол наклона секущей стремится к углу наклона касательной и этот угол равен углу МАС как односторонние при параллельных прямых АС и Ох.

Сравнивая определения производной и полученное выражение можно сделать вывод: k = ƒ’(х₀)

(слайд №6)

Геометрические смысл производной состоит в том, что значение производной функции в точке равно угловому коэффициенту касательной к графику функции в этой точке.

Пример 1: Найдите угловой коэффициент касательной к графику функции ƒ(х) = x³ с абсциссой в точке x₀ = 1

Пример 2: найдите угол между касательной к графику функции ƒ(х) = 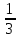x³ с абсциссой в точке x₀ = 1 и осью Ох

Выведем уравнение касательной к графику функции в точке х₀. (слайд № 7)

Если у=кх+b искомое уравнение, то к=ƒʹ(х₀). Уравнение примет вид: у=ƒʹ(х₀)х+b, b = у-ƒʹ(х₀)х, у = ƒ(х₀),

b = ƒ(х₀) - ƒʹ(х₀)х

У = ƒʹ(х₀)х + ƒ(х₀) - ƒʹ(х₀)х₀

y = f(x₀) + f’(x₀) (x - x₀) – уравнение касательной.

1. Найти ƒ(х₀)

2. Найти ƒʹ(х)

3. Найти ƒʹ(х₀)

4. Подставить полученные числа в уравнение касательной.

Пример 3: Построить касательную к параболе у = х² в точке х₀ = -1

Решение: 1) Построим параболу у=х², её вершина находится в точке (0,0), ветви направлены вверх.

2) составим уравнение касательной: ƒ(х₀) = ƒ(-1) = (-1)² = 1

ƒʹ(х) = (х²)ʹ = 2х, ƒʹ(х₀) = ƒʹ(-1) = 2ˑ(-1) = -2, у = 1-2(х+1), у = -2х-2, (0,-2), (1,-4)

3) Построим прямую.

В качестве примера на геометрический смысл производной можно рассмотреть так называемую задачу о прожекторе, которую коротко можно сформулировать так: какой формы должно быть зеркало? Где поместить источник света?

Для этого нужно ввести понятие параболоида вращения. Поверхность, получившаяся при вращении параболы у = х² вокруг оси Ох называется параболоидом. Представим себе, что внутренняя поверхность его – зеркальная и это параболическое зеркало освещается пучком лучей света, параллельных оси Оу. Рассмотрим сечение этого зеркала плоскостьюά, проходящей через ось Оу, Это сечение представляет собой такую же параболу у=х². Согласно законам оптики отраженный луч света будет лежать в плоскости άи этот луч образует с касательной такой же угол, как и падающий МА. Все лучи, параллельные оси Оу, после отражения пересекутся в одной точке, которая называется фокусом параболического зеркала. Если поместить в фокусе источник света, то отраженные лучи не будут рассеиваться, а соберутся в узкий пучок, параллельный оси зеркала. То есть, мы получаем возможность усилить световой сигнал. На этом свойстве основано устройство прожекторов и фонарей, различных проекторов. Если же вместо зеркала в фокусе разместить фотопластинку, то мы получим возможность световой сигнал идущий от звезды. На этом свойстве основано устройство параболических телескопов и параболических антенн, которые усиливают радиосигналы.

6. Первичное осмысление и закрепление связей и отношений в объектах изучения (15 мин)

1) Найти значения k и b, если прямая у = кх + b проходит через точку (x₀; y₀) и образует с осью Ох угол α: α = 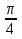, x₀ = - 3, y₀ = 2

2) Найдите угловой коэффициент касательной к графику функции ƒ(х) = 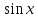с абсциссой в точке

x₀ =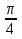

3) найдите угол между касательной к графику функции ƒ(х) =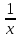 с абсциссой в точке x₀ = 1 и осью Ох

4) Написать уравнение касательной к графику функции ƒ(х) = x - 3x² с абсциссой в точке

x₀ =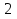

7. Постановка задания на дом (5 мин) Алимов Ш. А. Алгебра и начала анализа: 10-11 кл. §48, стр. 247-250, №860,

8. Подведение итогов урока (5 мин).

1)Что называется секущей и касательной?

2)В чём заключается геометрический смысл производной функции в точке?

3)Какое уравнение имеет касательная к графику функции в точке?