Конспект урока «Применение производной» по алгебре для 10 класса
 МБОУ «СОШ №2» г.Абакана
МБОУ «СОШ №2» г.Абакана
Учитель математики: Герасимова Ирина Андреевна
Интегрированный урок по теме «Применение производной»
Девиз урока: Скажи мне, и я забуду
покажи мне ,и я запомню
Дай действовать самому
И я научусь. Конфуций
Цели
Учебные:
-
Закрепить понятие физического смысла производной.
-
Показать межпредметную связь на примере математического моделирования.
-
Научить применять полученную модель на практике.
Воспитательные:
-
Обучение навыкам: планирования деятельности, работы в оптимальном темпе, подведения итогов.
-
Развитие умения оценивать свои способности, свое положение в группе, контактировать с товарищами.
-
Вызвать чувства ответственности и сопереживания.
Развивающие:
-
Обучение навыкам работы с компьютером.
-
Развитие умения находить нужную литературу, выполнять и оформлять исследовательскую работу.
-
Формирование «ключевых компетенций».
Оборудование
Компьютер, экран, проектор, раздаточный материал, творческие работы учащихся. Замечание
За 2 недели до урока класс разделен на 3 группы и назначены консультанты. В группу вошли учащиеся с разными учебными возможностями. Каждая группа получила задание приготовить презентацию «Применение производной для решения задач из различных областей науки».
I группа - «Применение физического смысла производной при решении физических задач»;
II группа - «Решение химических и биологических задач с помощью производной»;
III группа - «Решение задач с географическим содержанием».
IV группа - «Решение математических задач с помощью производной».
К началу урока столы в классе расставлены так, чтобы учащиеся могли работать по группам.
Ход урока
1.Организационный момент
Учитель формулирует тему и цели урока. Ученики записывают число и тему урока в тетрадях. Слайд №1(тема урока)
2.Актуализации знаний: Чтоб урок шел без запинки,
Начнем его с легкой разминки.
Математический кроссворд.
-
Знак обозначения действия сложения
-
Сумма длин всех сторон многоугольника
-
Геометрическая фигура, состоящая из двух лучей
-
Тригонометрическая функция
-
Часть прямой, заключенная между двумя точками
-
Равенство, содержащее переменную
-
Сотая часть числа
-
Единица измерения угла
-
Сторона прямоугольного треугольника, лежащая против прямого угла
-
Часть окружности, заключенная между двумя точками.
-
Одно из основных неопределяемых понятий стереометрии
| 9 | ||||||||||
| 5 | ||||||||||
| 6 | 8 | 10 | ||||||||
| 2 | 3 | 7 | 11 | |||||||
| 4 | ||||||||||
| 1 п | р | о | и | з | в | о | д | н | а | я |
Слайд № 2(после того ,как разгадали кроссворд, на слайде –ключевое слово)
3. Фронтальный опрос по теории (10 мин).
-
Что называется приращением аргумента.
-
Что называется приращением функции.
3. В чем состоит геометрический смысл производной функции.
4. В чем состоит механический смысл производной функции.
5. Дайте определение производной функции f(x) в точке х0
6. Основные формулы дифференцирования.
7. Уравнение касательной к графику функции.
Слайд №3-определение производной в стихах

4.Математический диктант
1) f(x) = 2х - 3 1) f'(x) = 12х3 - 21х2 + 4х
2) f(x) = 3х4 – 7х3 +2х2 +р 2) f'(x) =-8(3-4х)
3) f(x) = х3 + √2 3) f'(x) = -8х
4) f(x) = (3 – 4х)2 4) f'(x) = 2
5) f(x) = (х3 -2х)2 5) f'(x) = 2(3х2 – 2) (х3 – 2х)
6) f(x) =(1+2х)(1-2х) 6) f'(x) = sin (3x + р/4)
7) f(x) = 2 sin x 7) f'(x) = 5/ sin2 (2 – 5x)
8) f(x) = -1/3 cos (3x + р/4) 8) f'(x) = 6x2 – 9cos 3x
9) f(x) = ctg (2 – 5x) 9) f'(x) = 2 cos x
10) f(x) = 2x3 - 3 sin 3x 10) f'(x) = 3x2
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 4 | 1 | 10 | 2 | 5 | 3 | 9 | 6 | 7 | 8 |
номер функции
номер составляющей производной
10 – «5» 8 – 9 – «4» 6 – 7 – «3» 5 – 0 – «2»
Учащиеся в таблице сопоставляют функцию, и ее производную. Взаимопроверка друг друга (Слайд№4).
5. Физкультминутка.
Однажды великого греческого философа Сократа спросили о том, что, по его мнению, легче всего в жизни. Он ответил, что легче всего поучать других, а труднее – познать самого себя. Мы познаем окружающий нас мир. Но сегодня давайте заглянем в себя. Как мы воспринимаем окружающий мир? Как художники или как мыслители?
Психологический тест.
1). Переплетите пальцы рук. Большой палец правой или левой руки оказался у Вас сверху? Запишите результат буквами «Л» или «П».
2). Скрестите руки на груди (поза «Наполеона»). Кисть, какой руки оказалась сверху? Запишите результат.
3). Изобразите «бурные аплодисменты». Ладонь, какой руки у Вас сверху? Запишите.
Подведем итоги, учитывая, что результат «ЛЛЛ» соответствует художественному типу личности, а «ППП» - типу мыслителя.
(Эти различия связаны с функциональной асимметрией мозга человека: у «художников» более развитое правое полушарие и преобладает образное мышление, у «мыслителей» – соответственно – левое полушарие и логическое мышление).
Какой же тип мышления преобладает у Вас?
6.Презентация творческих работ учащихся. От каждой группы выходят к доске по два ученика, один из них садится за компьютер и демонстрирует работу, а другой представляет ее. В результате на доске и в тетрадях заполняется таблица.
| Обозначения | Понятие на математическом языке | |
| Относительный прирост в данный момент времени |
| Р = х′ ( t) |
| Средняя скорость химической реакции |
| V(t) = |
| Удельная теплоемкость тела |
| C(t) = Q′ (t) |
| Сила тока |
| I = = |
| ЭДС |
| E = - |
| Скорость точки в момент времени t |
| S |
| Ускорение точки в момент времени t |
| a(t) = v′(t) |
Работа в группах
Группам раздаются конверты, в которых лежат по 5 задач. Консультант раздает каждому ученику из своей группы по одной задаче. Через пять минут он организует обсуждение решенных задач в группе так, чтобы каждый смог объяснить их решение перед классом. Ещё через пять минут консультант собирает решения и сдает их учителю.
Задачи
№1
Координата материальной точки изменяется с течением времени по закону х(t) = 3t 2 - 7t + 6. Найдите скорость точки в момент времени t = 6.
№2
При движении тела по прямой его скорость V (м/с) меняется по закону V ( t ) = t 5 /5 - t 3 + t + l , где t - время движения в секундах. Найдите ускорение (м/с 2) через 2 секунды после начала движения.
№3
Найдите силу F , действующую на материальную точку с массой m , движущуюся прямолинейно по закону х( t ) = 2 t 3 - t 2 при t = 2.
№4
Известно, что для любой точки С стержня АВ длиной 20 см , отстоящей от точки А на расстоянии n , масса куска стержня АС в граммах определяется по формуле m ( n ) = 3 n 2 + 5 n . Найдите линейную плотность стержня: а) в середине отрезка АВ; б) в конце В стержня.
№5
В какие моменты времени ток в цепи равен нулю, если количество электричества, протекающего через проводник, задается формулой: а) q = t + k / t ; б) q = t -![]() + l .
+ l .
Проверка и обсуждение решенных задач
Готовые решения выводятся с помощью проектора на экран и учащиеся объясняют решение каждой из пяти задач (какая из задач и кого попросят её объяснять заранее неизвестно ни консультантам, ни учащимся). Решения всех задач учащиеся записывают в тетрадях.
Итог урока: Для выставления отметок за урок раздаются оценочные листы
Оценочный лист
| Отметка за презентацию (ставит консультант) | Сам. работа «ЕГЭ» (ставит учитель) | Работа в группе (ставит консультант) | Оценка за урок (ставит ученик) | Отметка за урок (ставит учитель) | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Условные знаки для оценивания учеником самого себя
О - Отлично изучил тему.
a - Есть пробелы, но я их решил самостоятельно.
N - Были пробелы, но я их решил с помощью группы.
// - Проблемы не решены.
Учитель ставит итоговую отметку, оценив деятельность всей группы.
Здесь представлен конспект к уроку на тему «Применение производной», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (10 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

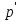
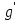
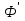 ( t)
( t) 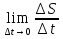
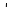 (
(