Презентация "Предел функции" по математике – проект, доклад
Презентацию на тему "Предел функции" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 22 слайд(ов).
Слайды презентации
Список похожих презентаций
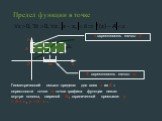
Предел функции в бесконечности и в точке
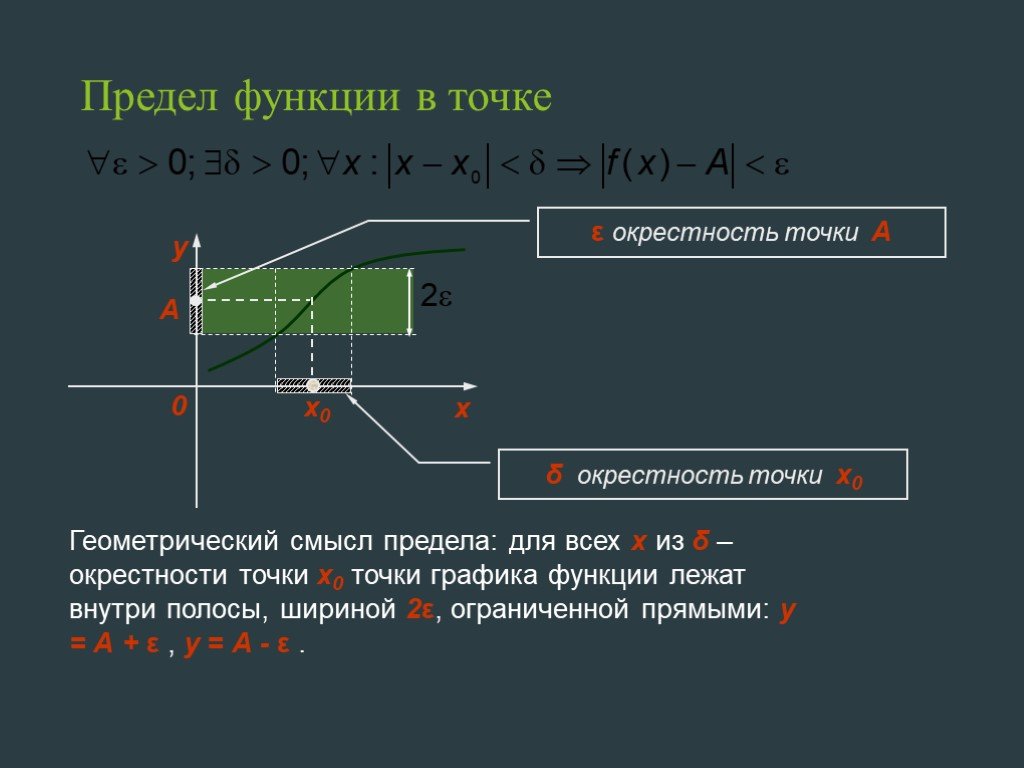
Число А называется пределом функции у=f(x), при х стремящемся к бесконечности, если для любого, сколь угодно малого числа ε>0, найдется такое положительное ...Предел функции в точке
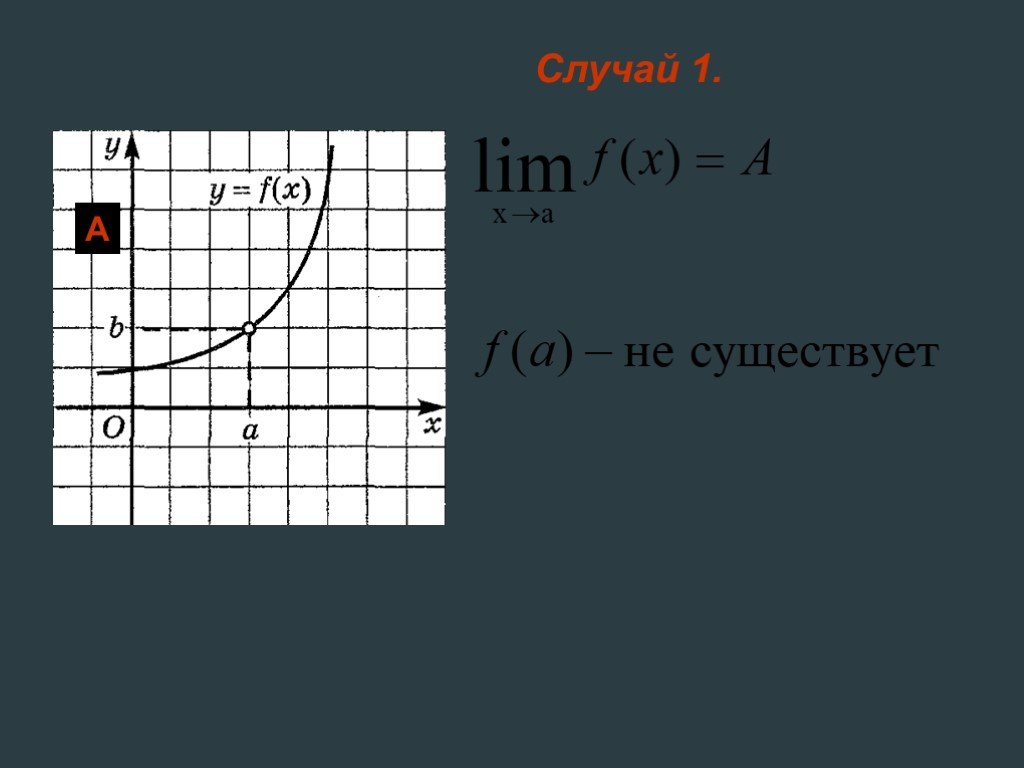
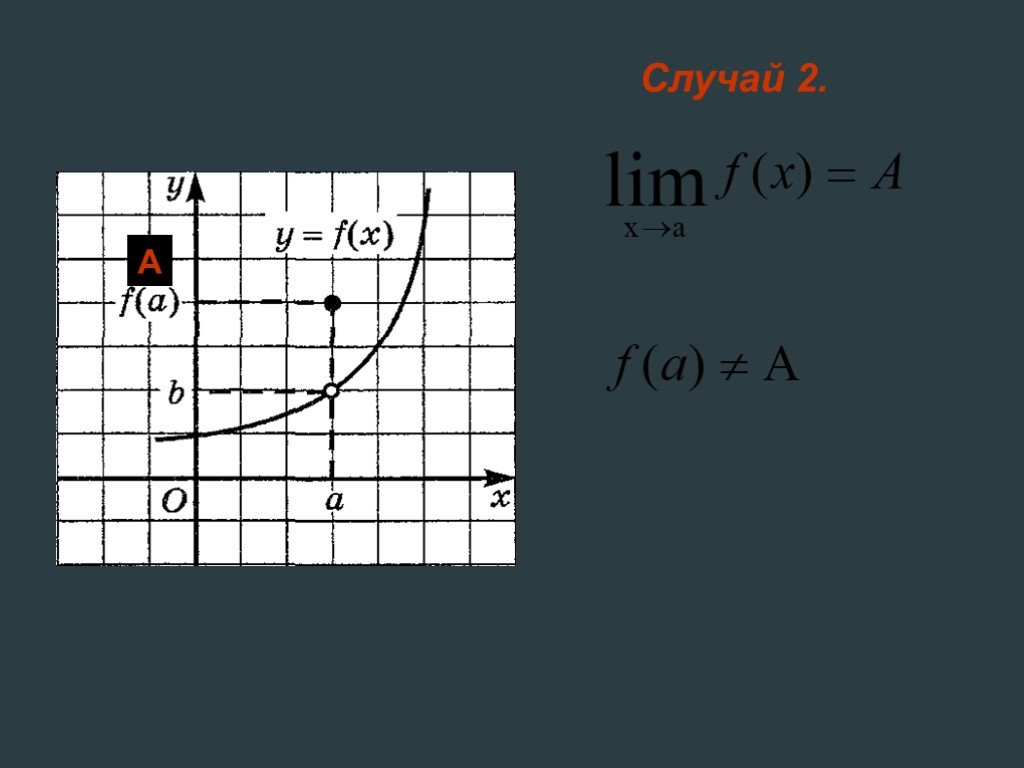
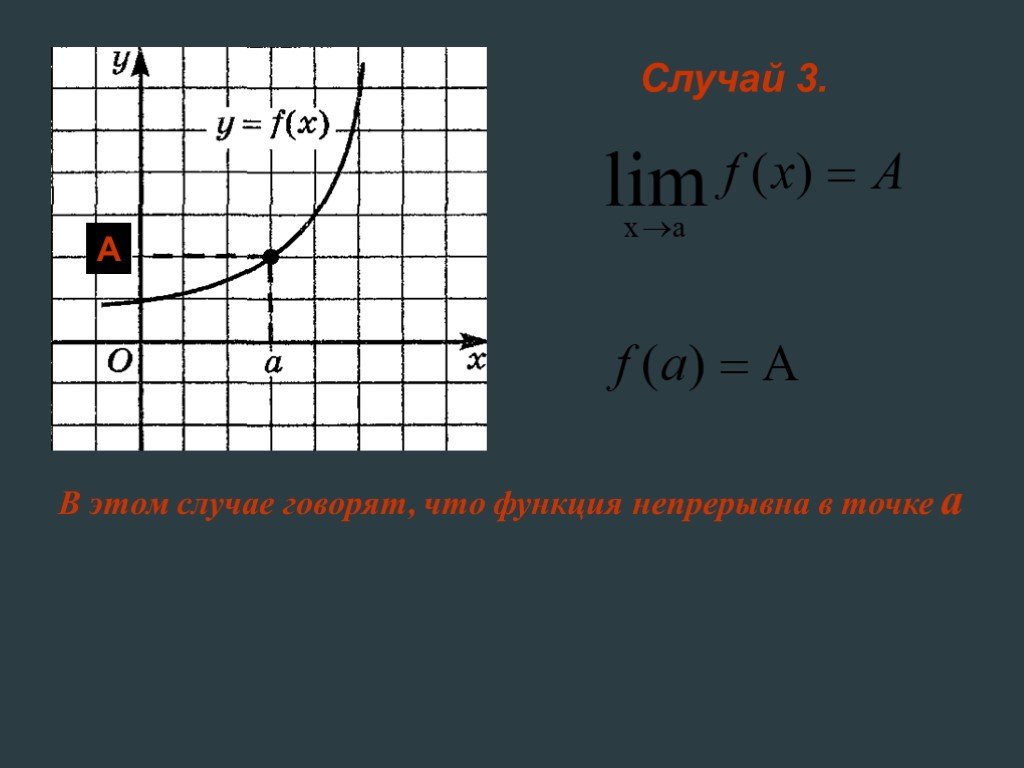
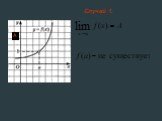
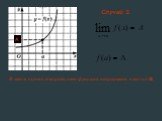
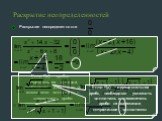
Рассмотрим функции, графики которых изображены на следующих рисунках:. Во всех трех случаях изображена одна и та же кривая, но все же изображают они ...Предел функции в точке
Одна и та же кривая, три разные функции. Отличие – поведение в точке х = а. f(a) – не существует, т.к. в точке х =а функция у = f(х) не определена. ...Понятие предела функции
Определение. Пусть функция f, принимающая действительные значения, определена в некоторой окрестности точки x0, кроме, быть может, самой точки x0. ...Область определения функции
. . Найдите область определения функции. Цель. Научиться находить область определения функции, заданной аналитически Задачи: построить алгоритм нахождения ...Определение линейной функции
Урок алгебры в 7 классе. Тема урока: Определение линейной функции. введение понятия линейной функции; отработка навыка распознавания линейной функции ...Определение производной от функции
Определение производной функции (Содержание). Геометрический смысл отношения Геометрический смысл отношения при Геометрический смысл производной функции ...Понятие обратной функции. Определение логарифмической функции
Рассмотрим пример какой-либо функции, заданной в явном виде формулой y=f(x). Пусть, для определенности, это будет линейная функция y=2x–7. Вспомним, ...Область определения и область изменения функции - Ограниченность функции
Укажите область определения функции. 17.08.2018. Устно:. Даны элементарные функции: Задайте сложную функцию:. Вычислите значение сложной функции:. ...Предел числовой последовательности
Содержание. Понятие числовой последовательности Примеры числовых последовательностей Способы задания последовательностей Ограниченность числовых последовательностей ...Алгоритмы - их функции и виды
Разветвляющийся алгоритм. Сюда пойдешь – клад найдешь. Сюда пойдешь – жену найдешь. Сюда пойдешь – мегабайт найдешь. Составить блок-схему алгоритма ...Построить график функции
Содержание:. 1. Функция y=sin x, её свойства и разновидности; 2. Функция y=cos x, её свойства и разновидности; 3. Примеры задач. 4. Закончить просмотр. ...Взаимно обратные функции
Цель проекта: Изучить поведение взаимно обратных функций. Установить связь графиков прямой и обратной функций. Подготовиться к успешной сдаче ЕГЭ. ...Возрастание и убывание функции
Числовые промежутки. [α;b] – отрезок (α;b) – интервал (α;b] – полуинтервал [α;b) - полуинтервал. Функция f(x) называется возрастающей на некотором ...Взаимное расположение графиков линейной функции
Разбейте функции, заданные формулами, на группы:. у = 2х - 3; у = х2 - 3; у = - 5х; у = 4 - 0,5х; у = - х +2; у=15х;. 7. 8. 9. 10. у = х (1 - х). ...Алгебра функции
Функции. Задания раздела направлены на проверку умений использовать графические представления для ответа на вопросы , связанные с исследованием функций. ...График степенной функции
Эпиграфом нашего урока являются слова А. Эйнштейна:. “Весь наш предшествующий опыт приводит к убеждению, что природа является осуществлением того, ...График линейной функции
График линейной функции. Цели урока:. Обучающие: 1. Учить строить график линейной функции; 2. Заполнять по графику таблицу значений х и у; 3. Изображать ...График линейной функции
1. Как называется функция у = - 2 х - 3? 2. Уравнение прямой линии имеет вид у = К х + b. Для функции у = – 7 + 2 х запишите, чему равны К и b. 3. ...График линейной функции
Проверка сплоченности космонавтов. y=x-4 y=-x+4 I вариант II вариант x y 1 2 0 -4 4. Формирование экипажей, посадка в космический корабль. 3 -1 -2 ...Конспекты
Предел функции в точке
Урок алгебры в 10 классе по теме «Предел функции в точке». Цель урока:. формирование у учащихся наглядно – интуитивных представлений о пределе ...Предел функции в точке, свойства. Бесконечно большие и бесконечно малые функции. Непрерывность функции
Министерство образования и науки Самарской области. . ГБОУ СПО «Безенчукский аграрный техникум». Конспект занятия. ТЕМА. Предел функции ...Вычисление пределов функции
План урока. Тема: «Вычисление пределов функции». Тип урока. – практическая работа. Цель:. закрепить и усовершенствовать практические приемы ...Область определения функции
Муниципальная общеобразовательная средняя школа № 14. Конспект урока по теме:. «Область определения функции». ...Определение числовой функции. Виды. Свойства, графики числовых функций. Способы задания функции
Кейс технологии. Урок алгебры. . Калинина Ирина Борисовна. учитель математики. МАОУ ГИМНАЗИЯ №8 г. Перми. РАЗРАБОТКА УРОКА. c. применением ...Определение числовой функции. Область определения, область значений функции
Муниципальное общеобразовательное учреждение. Оковецкая средняя общеобразовательная школа. Селижаровский район Тверская область. Тема урока:. ...Показательные функции, уравнения, неравенства
Обобщающий урок. по теме:. Учитель математики филиала. . БОУ ХМАО - Югры В(с)ОШ. при ИР 99/15 г.Нижневатовска. ...Применение производной к исследованию функции
Обобщающий урок в 11 классе по теме. «Применение производной к исследованию функции». Цель урока:. Систематизирование и обобщение знаний ...График квадратичной функции и модуль
Администрация города Улан - Удэ. Комитет по образованию. МАОУ «Средняя общеобразовательная школа № 25». Урок алгебры в 9 классе. ...Преобразование графика тригонометрической функции у = sin x путем сжатия и расширения
Предмет:. алгебра 10 кл. Тема урока:. «Преобразование графика тригонометрической функции у = sin. x. путем сжатия и расширения». Тип урока:. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:18 октября 2018
Категория:Математика
Содержит:22 слайд(ов)
Поделись с друзьями:
Скачать презентацию