Конспект урока «Определение числовой функции. Область определения, область значений функции» по алгебре для 9 класса

Муниципальное общеобразовательное учреждение

Оковецкая средняя общеобразовательная школа

Селижаровский район Тверская область

Тема урока: «Область определения функции»

Автор: Николаева Татьяна Николаевна, учитель I категории, МОУ Оковецкая сош

Предмет: Алгебра

Класс: 9

Тема: Определение числовой функции. Область определения, область значений функции.

Тип урока: изучение нового материала.

Оборудование: ПК, программа «Графики», презентация (тест в программе PowerPoint), индивидуальные карточки (задания на построение графиков, определения функции, данные учеными).

Цели урока:

Обучающие: ввести определение числовой функции, области определения и области значения функции; формировать навыки нахождения области определения и области значения функции.

Развивающие: развивать умение пользоваться изученным материалом для нахождения области определения функции; грамотную речь; развитие памяти; умений организации учебного труда; умение работать на компьютере.

Воспитывающие: формировать умение аккуратно и грамотно выполнять математические записи; воспитание воли и настойчивости у учащихся для достижения конечных результатов.

1. Орг. Момент.

Приветствие, проверка наличия учебных принадлежностей.

2. Мотивация.

С сегодняшнего урока мы начинаем изучать большую тему

« Числовые функции», на неё отводится 25 часов. Задания по этой теме встретятся на экзамене.

Наш сегодняшний урок состоит из пяти этапов.

1. Проверка домашнего задания.

2. Повторение (актуализация знаний).

3. Изучение нового материала.

4. Закрепление.

5. Тестирование.

III.

1 этап. Проверка домашнего задания.

Домашнее задание №7.4, 7.5 вы на перемене проверили по листу самоконтроля.

2 этап. Повторение.

1. При каких значениях х выражение имеет смысл?

Х+4, 2х²+3, 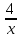, , 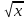, 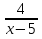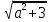(задания записаны на левом крыле доски)

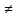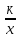2. Какие функции мы изучали в 7 и 8 классах? ( линейная: у=кх+b? квадратичная: ах² +bx+c, а0, у= , у=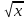

Практическая работа на компьютере (каждый ученик работает индивидуально на компьютере)

В программе «Графики» построить функции:

1. У=2х, у= -3х+4. Какие значения принимает х, у?

2. У= 2х²+4х-3, у=-3х-6х+2. Какие значения принимает х, у? Назвать вершину параболы, промежутки возрастания, убывания.

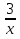3. У= , у=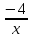 . Какие значения принимает х?

3 этап. Изучение нового материала.

1. Определение функции.

Плакат на доске:

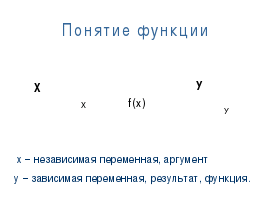
Если даны числовое множество Х и правило f , позволяющее поставить в соответствие каждому элементу х из множества Х определенное число у, то говорят, что задана функция у= f(х) с областью определения Х.

Пишут у= f(х), х⋴Х. При этом переменную х называют независимой переменной или аргументом, а переменную у – зависимой переменной.

Работа с учебником: самостоятельно прочитать правило на стр.86 учебника.

Историческая справка: Общее определение функции, которое мы называем теперь «классическим» сформировалось не очень давно – лишь в начале прошлого века. И хотя математики имели дело с различными конкретными функциями почти на каждом шагу развития науки, все же должен был пройден долгий путь отбора элементарных понятий и их обобщений, пока ученые пришли к необходимости общего определения функции и нашли его.

Экспериментальное задание. На столах лежат листы, на которых написаны определения функции, данные учеными в VIII- I веках.

Определение функции

Функция переменной величины есть аналитическое выражение, составленное из этой величины и постоянных.

И. Бернулли, 1718г.

Функция есть кривая, начертанная свободным влечением руки.

Л. Эйлер, 1748г.

Когда некоторые количества зависят от других таким образом, что при изменении последних изменяются и первые, то первые называются функциями вторых.

Л. Эйлер, 1755г.

Всякое количество, значение которого зависит от одного или многих других количеств, называется функцией этих последних, независимо от того, известно или нет, какие операции нужно произвести, чтобы перейти от них к первому.

С. Лукруа,1797г.

Функция от х есть число, которое дается для каждого х и вместе с х постепенно изменяется. Значение функции может быть дано или аналитическим выражением, или условием, которое подает средство испытывать все числа. Зависимость может существовать и оставаться неизвестной.

Н. Лобачевский, 1834г.

Y есть функция от х, если всякому значению х соответствует вполне определенное значение у, причем совершенно неважно, каким именно способом установлено указанное соответствие.

П. Дирихле, 1837г.

Сравните эти определения с определением, которое дано в учебнике. Какое из этих определений более соответствует определению функции на ваш взгляд? (выслушать ответы)

Вывод: Мы увидели, как совершенствовалось определение функции. И последняя его форма не означает конца истории. Можно не сомневаться, что и в дальнейшем под воздействием новых требований как самой математики, так и других наук определение функции будет изменяться. А эти изменения будут приводить к новым важным открытиям.

2. Определение области определения и множества значений функции.

Областью определения функции называют множество всех значений, которые может принимать ее аргумент.

Например: у= х+2 , Д(f)=(-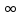;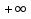) или х(-;)

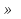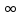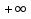У= 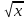, Д(f)=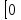;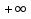) или х;)

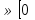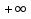Найти область определения функции, заданной формулой, - это значит найти все значения аргумента, при которых формула имеет смысл.

Множество всех значений функции у=f(х) называют областью (множеством) значений функции.

У=х+2 , Е(f)=(-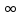;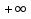) или у(-;)

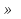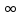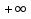У= х² , Е(f)=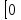;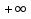) или у;)

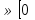4 этап. Закрепление.

№ 8.1(в) Ученики по одному выходят к доске,

8.3(в) комментируют решение

8.4(в)

8.5(в)

8.6(в)

8.16 (в) Объяснение учителя

5 этап. Тестирование.

Программа PowerPoint.

Критерии отметки: «5» - 8 заданий

«4» - 6,7 заданий

«3» - 4,5 заданий

IVДомашнее задание: § 8, определения, № 8.5(а), 8.6(а), 8.16(а);

стр.176 (повторение) №10,12

доп. задание для сильных об-ся: №8.25(а)

V. Итог урока:

1. Подведение учащихся к самостоятельным логическим выводам («Чему вы научились, какие новые определения узнали?»).

2. Оценивание.

Литература:

1. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся Общеобразовательных учреждений / [А.Г.Мордкович, Л.А.Александрова, Т.Н.Мишустина и др.]; под ред. А.Г.Мордковича. – 12-е изд., испр. - М.: Мнемозина, 2010.

2. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся Общеобразовательных учреждений / [А.Г.Мордкович, Л.А.Александрова, Т.Н.Мишустина и др.]; под ред. А.Г.Мордковича. – 12-е изд., испр. - М.: Мнемозина, 2010.

3. http://ru.wikipedia.org

4. www.intergu.ru

5. http://le-savchen.ucoz.ru/index/0-24

Примечание: в 9 классе 5 обучающихся. За компьютерное тестирование получили отметки «5» - 1 обучающийся; «4» - 4 обучающихся.