Конспект урока «Предел функции в точке» по алгебре для 10 класса

Урок алгебры в 10 классе по теме «Предел функции в точке»

Цель урока: формирование у учащихся наглядно – интуитивных представлений о пределе функции в точке.

Задачи урока:

• ввести понятие предела функции в точке;

• рассмотреть геометрическую иллюстрацию понятия предела функции в точке;

• ввести понятие непрерывности функции;

• рассмотреть правила о нахождении предела суммы, произведения и частного двух функций;

• рассмотреть примеры нахождения предела функции в точке.

Тип урока: урок объяснение нового материала.

План урока.

1. Организационный момент.

2. Мотивация изучения темы.

3. Подготовительная работа.

4. Изучение нового материала.

5. Решение задач.

6. Домашнее задание.

7. Итог урока.

Ход урока.

1. Организационный момент.

- Здравствуйте, ребята. Тема нашего урока: «Предел функции в точке». Сегодня на уроке мы познакомимся с понятиями «предел функции в точке», «непрерывность функции», а также рассмотрим правила вычисления предела функции в точке.

2. Мотивация изучения темы.

- Эта тема очень важна для дальнейшего изучения алгебры: понятие предела функции имеет большое значение для построения графиков функций. Кроме того, в дальнейшем мы будем изучать понятие производной и без знания предела функции рассмотрение этого понятия невозможно.

3. Подготовительная работа.

- Перед тем как начать изучать новую тему выполним следующее задание: постройте график функции если:

а) при х = 4 значение функции не существует; (рис.1)

б) при х = 4 значение функции равно 3; (рис.2)

в) при х = 4 значение функции равно 2. (рис.3)

(В ходе выполнения этого упражнения учащиеся повторяют нахождение области определения функции, а также построение графика функции, которая при данном значении аргумента либо имеет значение, либо не определена).

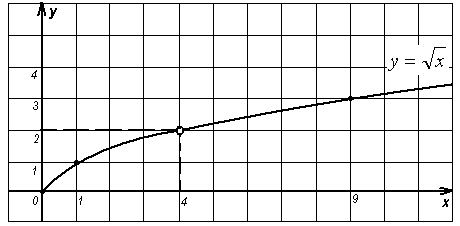
Рисунок 1

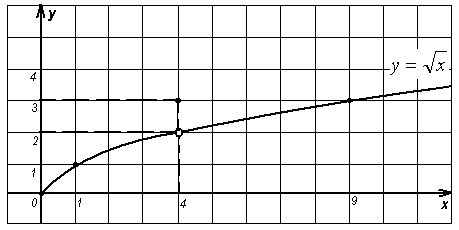
Рисунок 1

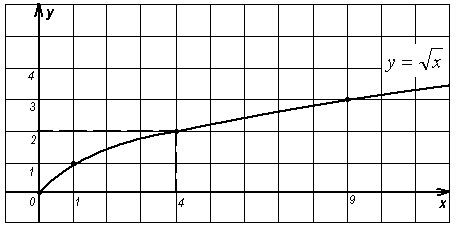
Рисунок 2

4. Изучение нового материала.

- Воспользуемся построенными графиками функций. Во всех трех случаях изображена одна и та же кривая, тем не менее, это три разные функции.

- Чем они отличаются друг от друга?

(Они отличаются друг от друга своим поведением в точке х = 4).

- Как ведет себя функция в точке х = 4 на первом графике?

(Для функции при х = 4 значение функции не существует, функция в указанной точке не определена).

- Как ведет себя функция в точке х = 4 на втором графике?

(Для функции при х = 4 значение функции существует, но оно отличается от естественного значения функции в указанной точке).

- Как ведет себя функция в точке х = 4 на третьем графике?

(Для функции при х = 4 значение функции существует, и оно равно естественному значению функции в указанной точке, то есть двум).

- Если мы исключим точку х = 4 из рассмотрения, то все три функции будут тождественными.

- Для всех трех случаев используется одна и та же запись: .

- В общем случае эта запись выглядит следующим образом: .

- Эту запись читаем так: «предел функции y=f(x) при стремлении х к а равен b».

- А теперь ответьте на такой вопрос: какую из трех рассмотренных функций естественно считать непрерывной в точке х = 4?

(Непрерывной будет третья функция)

- Так как эта функция непрерывна, то она удовлетворяет условию . И функцию f (x) называют непрерывной в точке х = а.

- Иными словами, функцию y = f (x) называют непрерывной в точке х = а, если предел функции y = f (x) при стремлении х к а равен значению функции в точке х = а.

- Функция y = f (x) называется непрерывной на промежутке Х, если она непрерывна в каждой точке промежутка.

- При изучении различных функций (линейной, квадратичной, степенной, иррациональной, тригонометрических) мы отмечали, что они являются непрерывными либо на всей числовой прямой, либо на промежутке. Исходя из этого, можно сформулировать следующее утверждение: если выражение f (x) составлено из рациональных, иррациональных, тригонометрических выражений, то функция y = f (x) непрерывна в любой точке, в которой определено выражение f (x).

5. Решение задач.

- Для закрепления понятия предела функции в точке выполним номер 678.

№ 39.18. Какая из функций, графики которых изображены на рис. 74 – 81, имеет предел при х  3? Чему равен этот предел?

Решение.

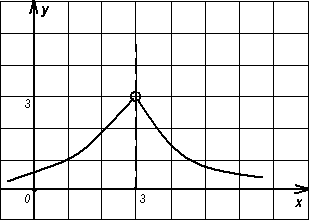
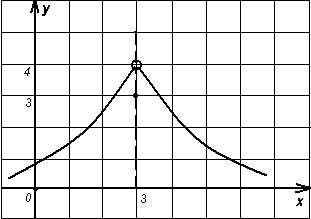
Рисунок 74 Рисунок 75

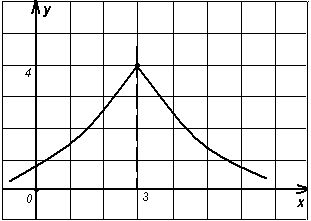
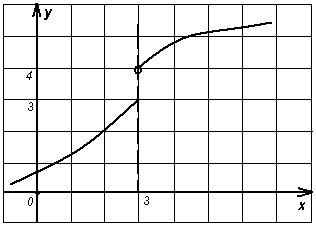
Рисунок 76 Рисунок 77

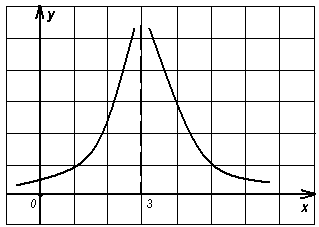
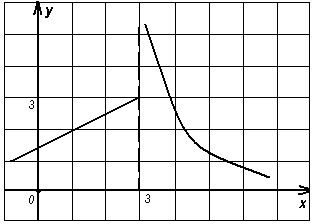
Рисунок 78 Рисунок 79

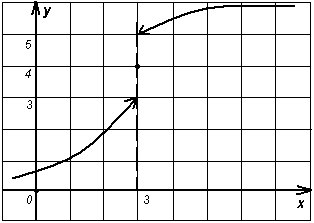
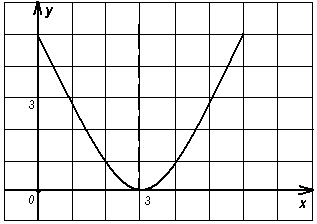
Рисунок 80 Рисунок 81

- Решим номер 39.19 (а, б).

№ 39.19 (а, б). Постройте график какой – нибудь функции y = g (x), обладающей заданным свойством:

а) , (рис.4)

б) . (рис.5)

Решение.

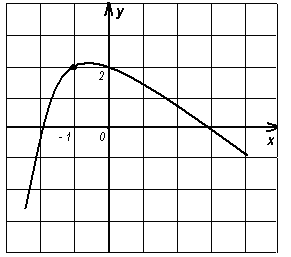
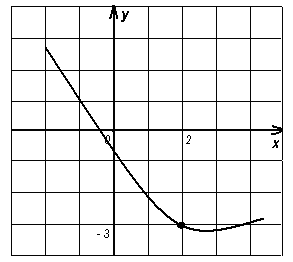
Рисунок 3 Рисунок 4

- Рассмотрим несколько примеров на вычисление пределов функций.

Пример 1. Вычислить: .

Решение. Выражение х³ – 2х² + 5х + 3 определено в любой точке х, в частности, в точке х = 1. Следовательно, функция у = х³ – 2х² + 5х + 3 непрерывна в точке х = 1, а потому предел функции при стремлении х к 1 равен значению функции в точке х = 1.

Имеем: .

Ответ: 7.

- Для решения следующего примера нам потребуются правила вычисления предела функции в точке.

Правило 1. .

Правило 2. .

Правило 3. .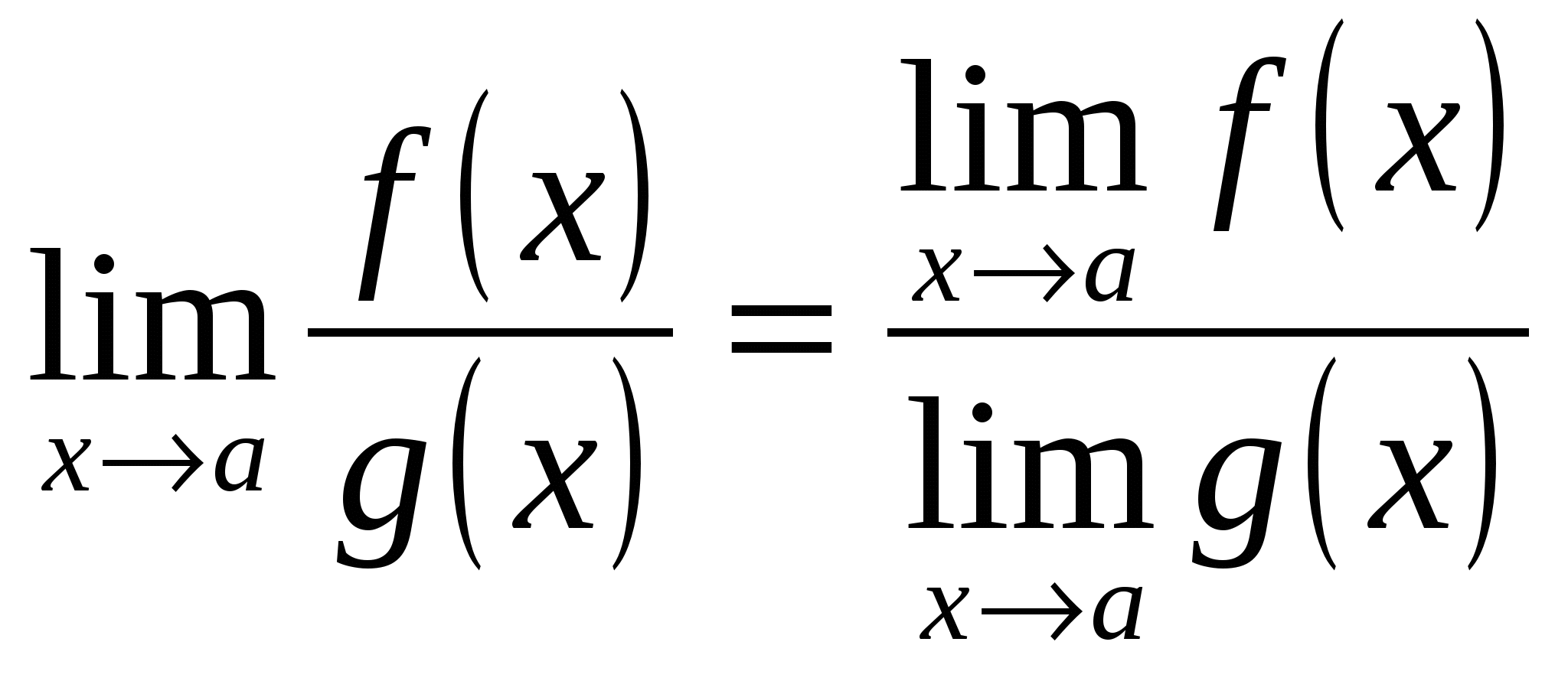

Пример 2. Используя эти правила, вычислим .

Решение. Выражение определено в любой точке х  0, в частности, в точке х = 2. Следовательно, функция у = f (x) непрерывна в точке х = 2, а потому предел функции при стремлении х к 2 равен значению функции в точке х = 2. Имеем: .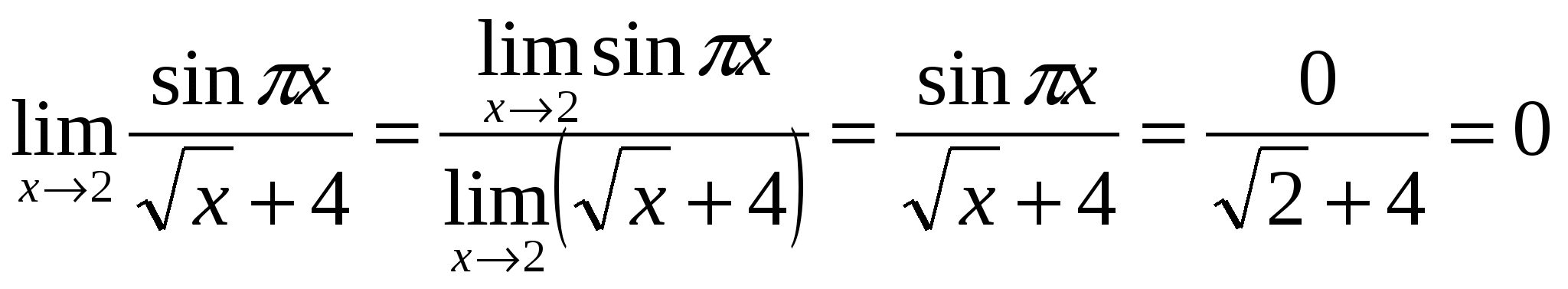

Ответ: 0.

- Решим номер 39.23.

№ 39.23. Вычислите: а) ;

б) ;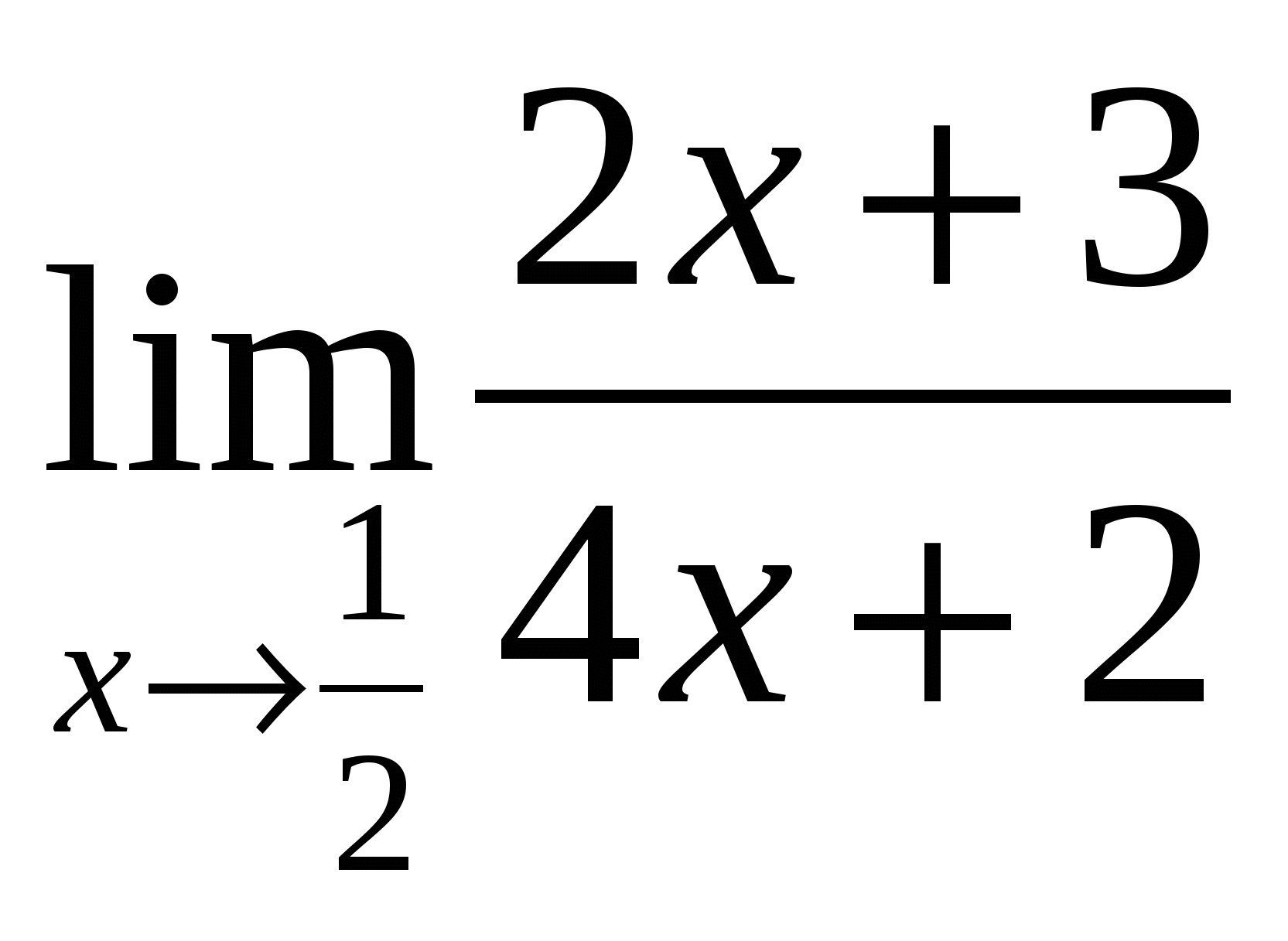

в) ;

г) .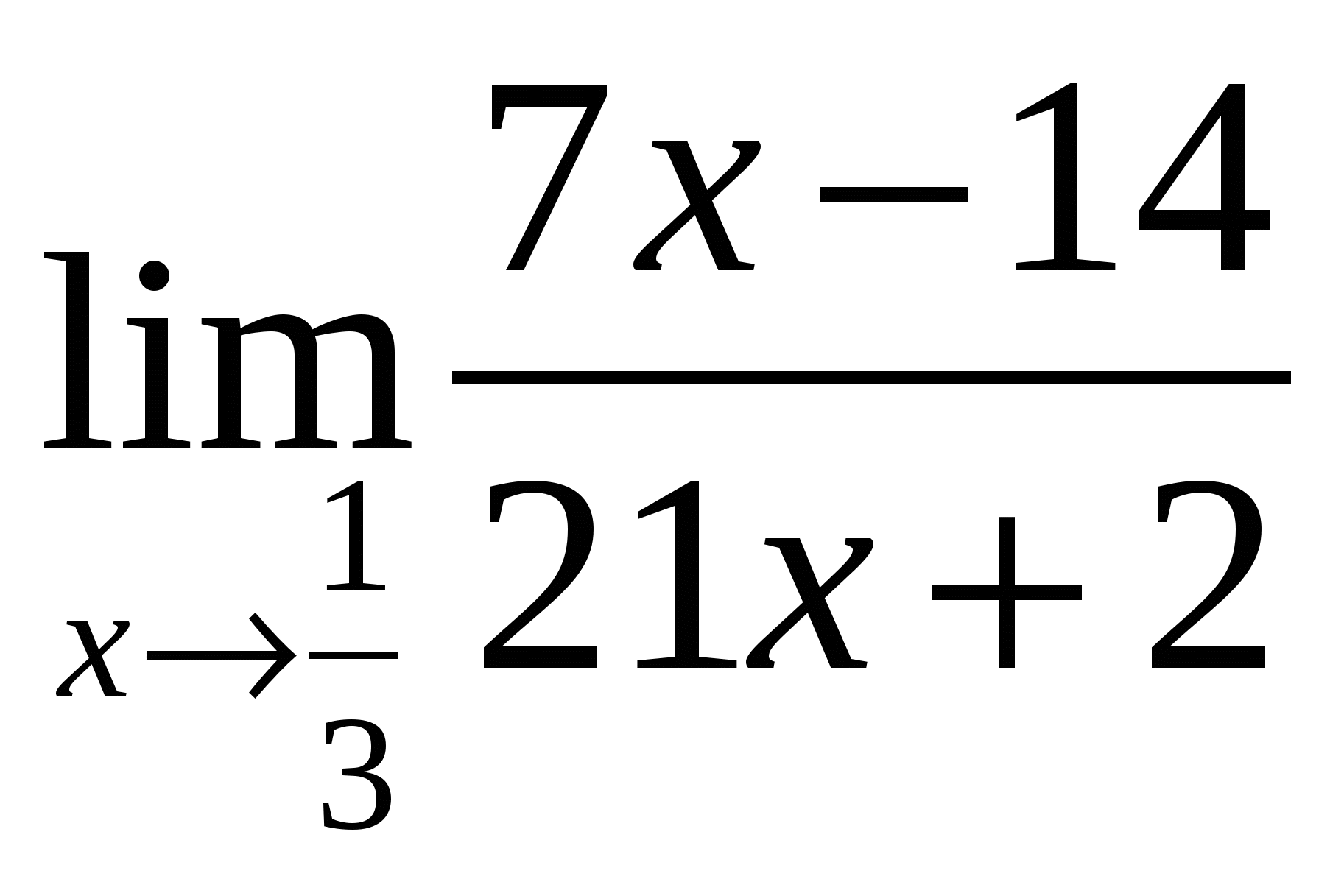

Решение.

а) . Выражение х² – 3х + 5 определено в любой точке х, в частности, в точке х = 1. Следовательно, функция у = х² – 3х + 5 непрерывна в точке х = 1, а потому предел функции при стремлении х к 1 равен значению функции в точке х = 1.

Имеем: .

Ответ: 3.

б) 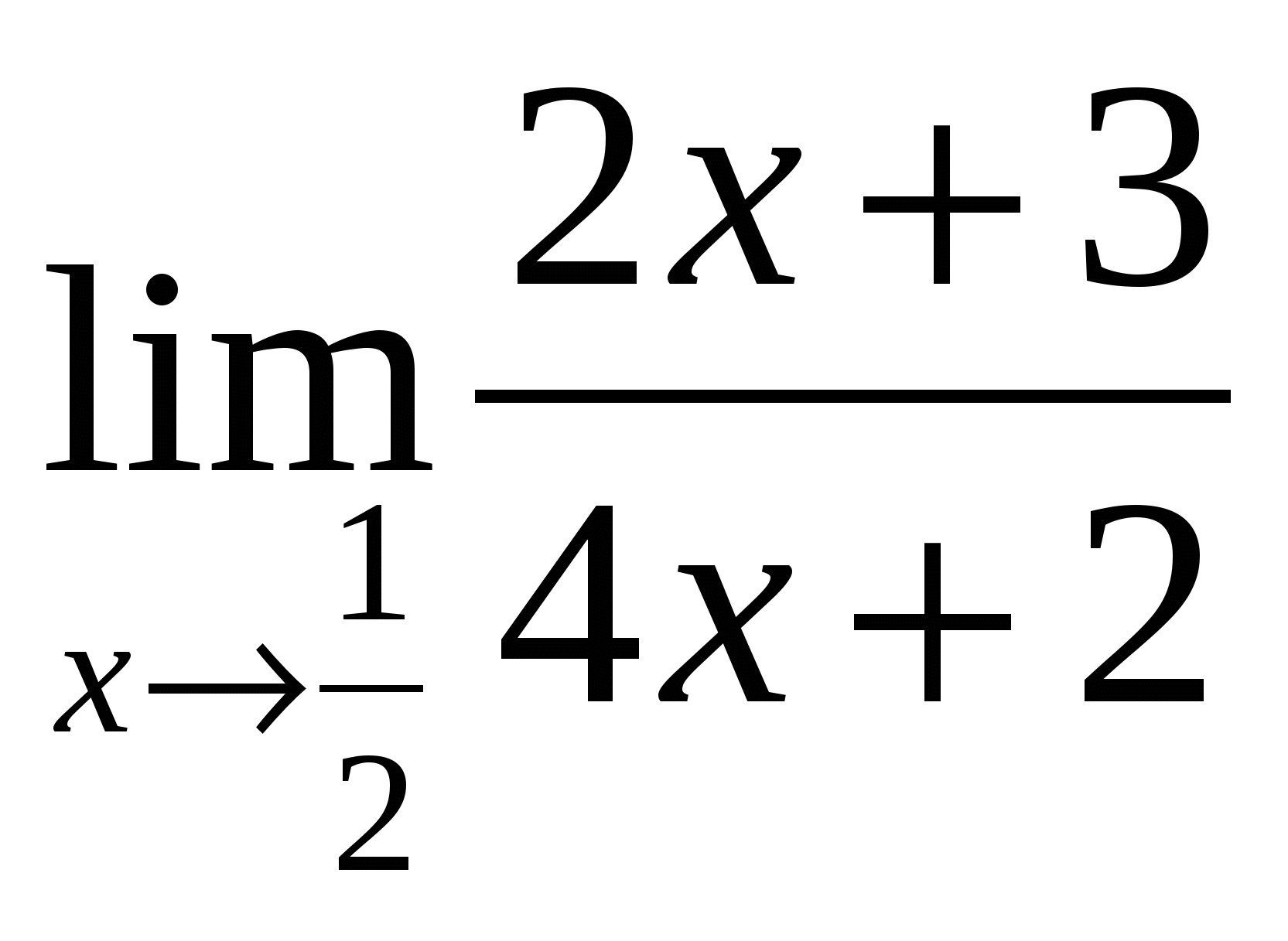. Выражение определено в любой точке х  , в частности, в точке х = . Следовательно, функция у = f (x) непрерывна в точке х = , а потому предел функции при стремлении х к равен значению функции в точке х = . Имеем: .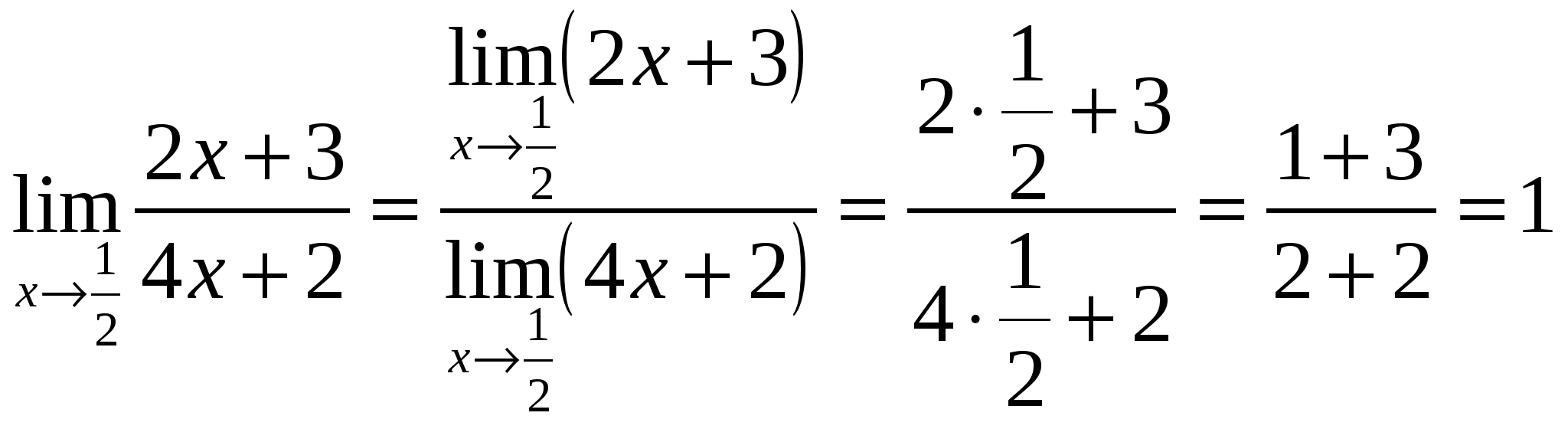

Ответ: 0.

в) . Выражение х² + 6х – 8 определено в любой точке х, в частности, в точке х = - 1. Следовательно, функция у = х² + 6х – 8 непрерывна в точке х = - 1, а потому предел функции при стремлении х к - 1 равен значению функции в точке х = - 1.

Имеем: .

Ответ: - 1.

г) 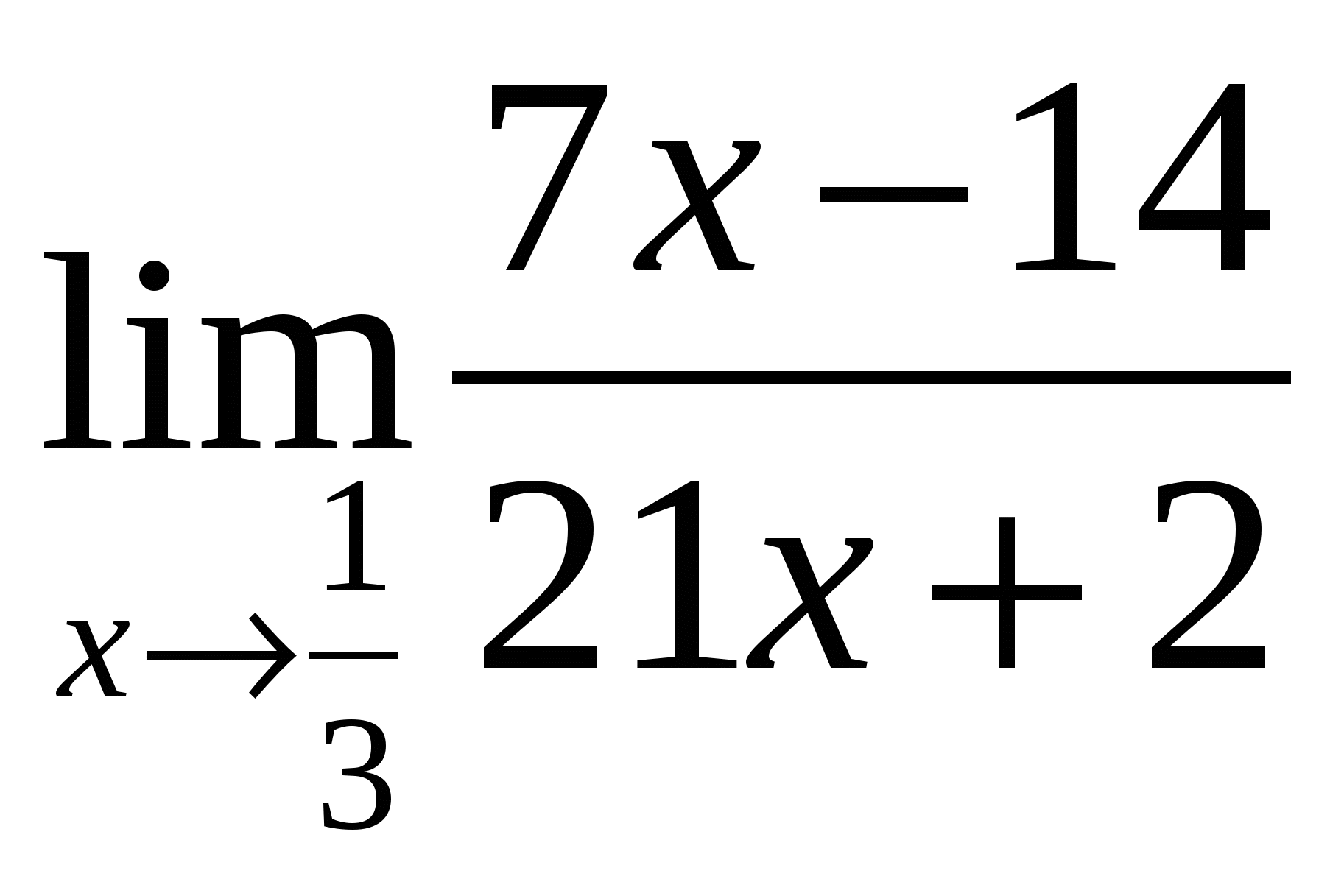. Выражение определено в любой точке х  , в частности, в точке х = . Следовательно, функция у = f (x) непрерывна в точке х = , а потому предел функции при стремлении х к равен значению функции в точке х = .

Имеем: .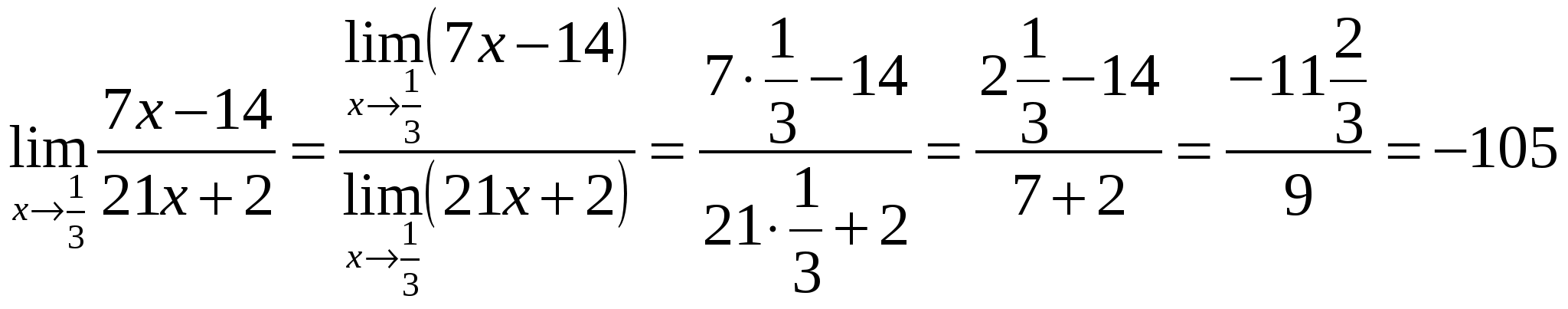

- Вы заметили, что в рассмотренных примерах вычисление пределов не составило значительных сложностей: достаточно было найти значение функции в точке, к которой стремится аргумент х. Но часты случаи, когда этот прием не срабатывает.

Пример 3. Вычислить .

Решение. Если подставить значение х = - 3 в заданное выражение, то и в числителе, и в знаменателе получится 0, а на нуль делить нельзя. Но заданную алгебраическую дробь можно сократить: .

Значит, функции и тождественны при условии х  - 3. Но при вычислении предела функции при х  - 3 саму точку х = - 3 можно исключить из рассмотрения. Значит, .

Ответ: - 1,5.

- Решим номер 39.27.

№ 39.27. Вычислите: а) ;

б) ;

в) ;

г) .

Решение.

а) . Если подставить значение х = 0 в заданное выражение, то и в числителе, и в знаменателе получится 0, а на нуль делить нельзя. Но заданную алгебраическую дробь можно сократить: .

Значит, функции и тождественны при условии х  0, х  1. Значит, .

Ответ: 0.

б) . Если подставить значение х = - 1 в заданное выражение, то и в числителе, и в знаменателе получится 0, а на нуль делить нельзя. Но заданную алгебраическую дробь можно сократить: .

Значит, функции и тождественны при условии х  0, х  - 1. Значит, .

Ответ: - 1.

в) . Если подставить значение х = 3 в заданное выражение, то и в числителе, и в знаменателе получится 0, а на нуль делить нельзя. Но заданную алгебраическую дробь можно сократить: .

Значит, функции и тождественны при условии х  3. Значит, .

Ответ: 3.

г) . Если подставить значение х = - 5 в заданное выражение, то и в числителе, и в знаменателе получится 0, а на нуль делить нельзя. Но заданную алгебраическую дробь можно сократить: .

Значит, функции и тождественны при условии х  0, х  - 5. Значит, .

Ответ: - .

6. Домашнее задание.

- Открываем дневники и записываем домашнее задание: номера 39.19 (а, б), 39.24, 39.28. Эти номера подобны тем, которые мы решали в классе, образец записи у вас в тетрадях.

7. Итог урока.

- Сегодня на уроке мы познакомились с понятием предела функции, непрерывности функции в точке и на промежутке, правила вычисления предела в точке, научились вычислять предел функции в точке.