Конспект урока «Решение уравнений» по алгебре для 6 класса
Тема урока: Решение уравнений
(урок контроля развивающей направленности)
Цели:
-
Формирование навыков при решении уравнений, диагностика усвоения знаний и умений при решении уравнений;
-
Формирование способности к самооценке выполненной деятельности;
-
Развитие памяти, внимания, познавательной активности и сообразительности;
-
Воспитание чувства ответственности за качество и результат выполняемой работы.
Задача урока:
Каждый должен разобраться в том, как он усвоил данную тему и если еще потребуется доработать то, что еще не получается.
Оборудование:
Дорофеев Г.В., Петерсон Л.Г. Математика. 6 класс, рабочие тетради и тетради с домашней работой, плакаты, высказывания.
Высказывание на доске:
Уравнение представляет собой наиболее серьезную и важную вещь в математике.
Лодж.
Ход урока
1. Самоопределение к деятельности
Демонстрация лица собаки в цифрах.
Задание: Распознать цифры, из которых составлена собака и найти их сумму. (Ответ: 39)
П лакат.
лакат.
2. Актуализация знаний и фиксация затруднений в деятельности
И как-то проще думать мне
Яснее стало в голове
Решенье легче постигать
Когда в уме умеешь ты считать
1. Упрости выражение, и найти модуль коэффициента
-
- 3 m ∙ (- 7 k) = 21 km 21 -- у
-
- 4 y ∙ 4,5 x = - 18 xy 18 -- р
-
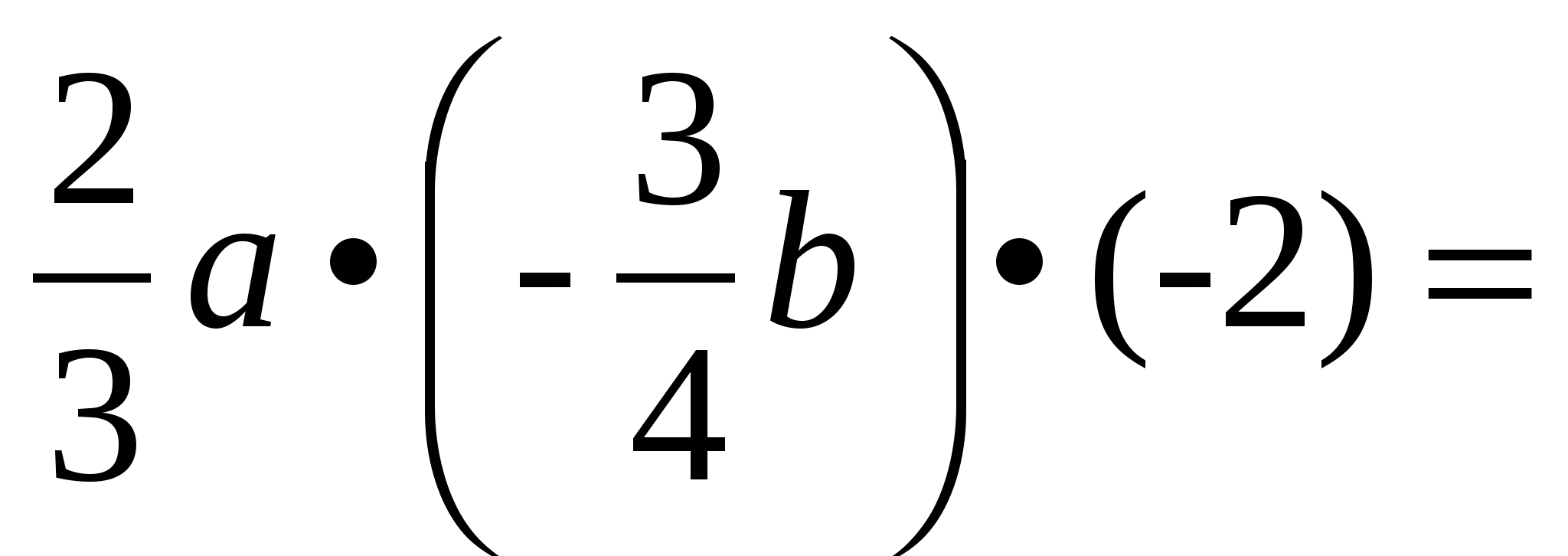 a b 1 -- а
a b 1 -- а -
- 9 x + 7 x – 5 x + 4 x = - 3 x 3 -- в
2. Найти значение переменной и ее модуль
-
х + (-10) = 5 х = 15 15 – н
-
х : (-2) = - 3 х = 6 6 – е
-
3 ∙ х = - 45 х = - 15 15 – н
-
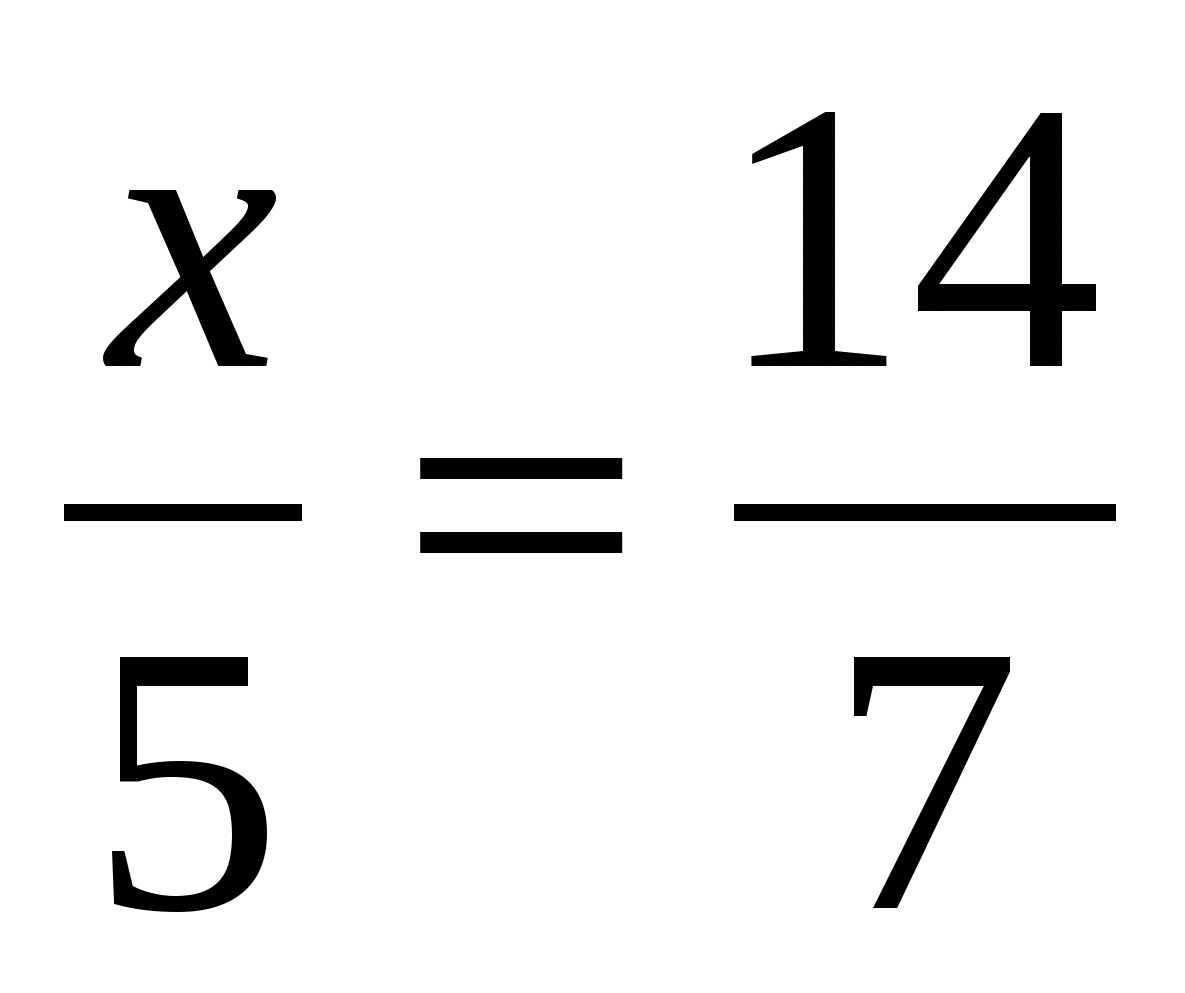 х = 10 10 – и
х = 10 10 – и -
2 х – 5 = х + 1 х = 6 6 – е
Поставить в соответствии числу букву из карточки и прочитать ключевое слово нашего урока: Уравнение.
У каждого на столе карточки
 Опрос по теории.
Опрос по теории.
Учитель: Дайте определение уравнения.
Предполагаемый ответ ученика: Уравнение это равенство, содержащее неизвестное значение которого надо найти.
Учитель: А что значить решить уравнение?
Предполагаемый ответ ученика: Это значить найти его корни или доказать, что их нет.
Учитель: А что такое корень уравнения?
Предполагаемый ответ ученика: Значение переменной, при которой уравнение обращается в верное числовое равенство.
Учитель: А кто, исходя из устной работы, скажет, чем же мы будем заниматься сегодня на уроке?
Предполагаемый ответ ученика: Решением уравнений.
Учитель: Значит, сформулируем тему нашего урока.
Предполагаемый ответ ученика: Решение уравнений.
Учитель: Открыли тетради и записали число и тему урока. А скажите этот урок у нас первый?
Предполагаемый ответ ученика: Нет
Учитель: А какие цели мы можем перед собой поставить?
Предполагаемый ответ ученика: 1. Отработать навыки решения уравнений.
2. Проверить свои умения по теме.
Учитель: А задача каждого из нас разобраться в том, как он усвоил данную тему.
А теперь вспомним, какие правила помогают нам решать уравнения? (правила в виде плакатов вывешиваются на доску).
Предполагаемые ответы учеников:
-
Нахождение неизвестных компонентов
-
Основное свойство пропорции
-
Упрощение уравнений. Приведение подобных слагаемых.
-
Перенос слагаемых
Плакаты
Нахождение неизвестных компонентов
Основное свойство пропорции
Упрощение уравнений. Приведение подобных слагаемых.
Перенос слагаемых
Учитель: Молодцы! А теперь каждый из вас будет учителем и проверит домашнее задание одного из учеников. (На доске записаны уравнения, в которых нарушены правила решения уравнений. Задача учеников объяснить какое правило нарушено и дать правильный ответ.)
1) 8 m + m – 7 = 38; 9 m = 38 + 7;
2 m = 38; 9 m = 45;
m = 38 : 2; m = 5.
m = 19. Правильный ответ. m = 5.
Ответ. m = 19.
Предполагаемый ответ ученика: Правильный ответ. m = 5. Нарушено правило: Упрощение уравнений. Приведение подобных слагаемых.
2) 5 х + 26 = 3 х + 4;
5 х – 3 х = 26 + 4; 5 х – 3 х = 4 – 26;
2 х = 30; 2 х = - 22;
х = 15. х = - 11.
Ответ. х = 15. Правильный ответ. х = - 11.
Предполагаемый ответ ученика: Правильный ответ. х = - 11. Нарушено правило: Перенос слагаемых,
26 должно быть со знаком минус.
Учитель: Пришло время проверить ваше домашнее задание. Откройте тетради с домашней работой. Кто решал первый вариант?
Ученики поднимают руки.
Учитель: Какое слово у вас получилось?
Ученик: Диофант.
Учитель: Кто решал второй вариант?
Ученики поднимают руки.
Учитель: Какое слово у вас получилось?
Ученик: Диофант.
Учитель: Кто решал третий вариант?
Ученики поднимают руки.
Учитель: Какое слово у вас получилось?
Ученик: Диофант.
Учитель: Молодцы! А есть ли те у которых получилось другое слово или оно не получилось вообще? ( Если есть такие учащиеся, то с ними ведется индивидуальная работа после урока.)
Домашнее задание (выдается накануне и содержит дифференцированный подход).
Вариант 1 « на 3»
Д 3 х = 75
Ф 3 х – 5 = 16
О 5 + 20 х = 15 + 30 х
Т 7 ( х – 3 ) = 49
А - 1,5 х – 9 = 0
Н 7= 6 – 0,2 х
И ![]()
| 5 | - 1 | 7 | - 6 | - 5 | 10 | |
| | | | | | | |
Вариант 2 « на 4»
Т - 6 х = - 84
И 48 – 3 х = 0
Ф 5 ( х – 3 ) = 80
О - ( у + 4 ) – 19 = 7
Д 11 х + 5 = – 12 + 5 х – 7
Н 6 ( х + 4 ) = 3 – х
А ![]()
| 16 | - 30 | 19 | 3,75 | - 3 | 14 | |
| | | | | | | |
Вариант 3 « на 5»
Ф ![]()
Т 3 х – 8 = х + 6
А х + 5 – ( 2 х – 2 ) = 6
Д 7 у – 20 = 2 – 4 у
О 5 х + ( 3 х – 3 ) = 6 х + 12
Н 7 – 2 ( х – 4,5 ) = 6 – 4 х
И ![]()
| - 3 | 7,5 | 3,6 | 1 | - 5 | 7 | |
| | | | | | | |
Вывешивается портрет Диофанта и ученик дает краткую историческую справку о нем.
Плакат.

3. Постановка проблемы.
Учитель: Английский поэт Джефри Чосер заявляет: Посредством уравнений, теорем
Я уйму всяких разрешил проблем.
А следующим заданием мы проверим имеются ли у вас проблемы при решении уравнений и какие.
| Самостоятельная работа Вариант 2 1. Приведите подобные слагаемые 5 у – 8 + 4 у + 2 2. Раскройте скобки – 2 (2 b + а – 5 ) 3. Раскройте скобки и приведите подобные слагаемые – 7 ( 4 с + 8 ) – ( 4 с – 9 ) 4. Решить уравнение
5. Решить уравнение - 12 х - 3 = - 11 х + 3 |
4. Первичное закрепление, обсуждение типовых затруднений
На доске записать краткое решение и верные ответы к заданиям. После выполнения учащиеся меняются тетрадями между собой и проверяют работу соседа. Ставят оценки.
П «5» - нет ошибок «4» - одна ошибка «3» - две ошибки
Учитель: Кто получил «5»?
Ученики поднимают руки.
Учитель: Умнички.
Учитель: А есть те кто сделал ошибки?
Ученики поднимают руки.
Учитель: В каких заданиях.
Учитель и ученики вместе выясняют в каких заданиях большее число ошибок и разбирают на доске эти задания. ( Одно или два задания. Остальное индивидуальная работа после урока.)
5. Самоконтроль с самопроверкой.
Учитель: Те, кто получил «5» берут розовые карточки и выполняют самостоятельно задание на них. С остальными ведется работа на доске над заданиями из самостоятельной работы. Предложить можно следующие задания:
1) 6 х – 7 + 8 у – 3 + 4 у – 10 х
2) – 6 ( – 3 х + 4 у – 8 )
3) 5 ( х – 1 ) + 2 ( х + 3 ) – 7 х
4) ![]()
5) 6 – 2 у = 18 – 3 у
Розовые карточки:
Вставь пропущенное число
(Подсказка: пропущенное число
связано с корнями уравнений)

1
35 – 3 х = 2 ![]() 25 – 4 х = 13
25 – 4 х = 13
5 х – 12 = 63 ? 4 х + 5 = 37

2
7 х + 11 = – 10 – 5,5 4 х + 7 = – 3
– 8 х – 21 = 1 ? – х + 2,5 = 9

3
8 х – 4 = 24 + х 1,4 х + 6 = – 1 3 х – 1,5 = 3
20 – 25 ?
Физпауза. Потрудились славно, отдохнем исправно,
Вот минутка для игры или физзарядки.
Учитель: Около 90 % всей информации человек воспринимает глазами. Если ваши глаза устают, то снижается ваше внимание и активность. Давайте перед следующими заданиями дадим глазам и себе отдохнуть. Звучит тихая медленная музыка и выполняется комплекс упражнений.
Примерный комплекс:
-
Закрыть глаза на несколько секунд, сильно напрягая глазные мышцы, затем раскрыть их, расслабив мышцы. Повторить 3-4 раза.
-
Посмотреть на переносицу и задержать взор. Затем посмотреть вдаль. Повторить 3- 4 раза.
-
Медленные наклоны головы: вперёд – влево – вправо – назад. Повторить 3-4 раза.
-
Поморгать несколько раз глазами, не напрягая мышц. Сделать глубокий вздох и медленный выдох.
6. Повторение и отработка навыков.
Учитель (читает высказывание на доске):
Уравнение представляет собой наиболее серьезную и важную вещь в математике. Лодж.
Вызывает ученика к доске для решения уравнения с полным объяснением.
Из учебника № 96 (е).
0,6 (-2к + 3) – 0,4 (9 – к) = - 0,3 ( к – 9); / ∙ 10 (сделаем коэффициенты целыми числами)
6 (-2к + 3) – 4 (9 – к) = - 3 ( к – 9); (раскроем скобки)
- 12 к + 18 – 36 + 4 к = - 3 к + 27; (приведем подобные слагаемые)
- 8 к – 18 = - 3 к + 27; (перенесем слагаемые с неизвестными в одну часть, а известные в другую)
- 8 к + 3 к = 27 + 18;
- 5 к = 45;
к = 45 : ( - 5);
к = - 9.
Ответ. к = - 9.
Учитель: Спасибо.
Один из помощников учителя делает анализ решения и ставит оценку, учитель соглашается с оценкой, если нет, то дает свой анализ и ставит оценку.
7. Повторный самоконтроль.
Учитель: Мы с вами сегодня на уроке решали различные уравнения и выполняли преобразования выражений, которые помогают нам решать уравнения. Сейчас мы проведем итоговый тест. Вам необходимо выполнить все задания и сложить результаты. Сумму результатов записать. Она и даст ответ на вопрос: Все ли у вас решено правильно?
Итоговый тест
Вариант 1
-
Приведите подобные слагаемые:
4 а + 5 b – 6 a – 4 b + 10 a
| 3) 20 a + 18 b | |
| 2) 8 a + 9 b | 4) 8 a + b |
-
Решите уравнение:
2,6 у = - 3,51
| 3) у = 0,52 | |
| 2) у = | 4) у = |
-
Решите уравнение:
4 – 3 у = 7 – у
| 3) у = - 1,5 | |
| 2) у = | 4) у = |
-
Решите уравнение:
![]()
![]()
| 3) х = 4 | |
| 2) х = - 4 | 4) х = - 26 |
-
Решите уравнение:
3 ( х – 1 ) = 2 ( 2 – х ) + 6
| 3) х = | |
| 2) х = | 4) х = |
Итоговый тест
Вариант 2
-
Приведите подобные слагаемые:
6 х – 7 у + 8 х – 7 у + 4 у
| 3) 2 х + 18 у | |
| 2) 2 х – 10 у | 4) 14 х – 10 у |
-
Решите уравнение:
- 1,2 х = 6,42
| 3) х = - 5,35 | |
| 2) х = | 4) х = - 0,52 |
-
Решите уравнение:
3 у – 3 = 5 – у
| 3) у = 1 | |
| 2) у = - 4 | 4) у = - 1 |
-
Решите уравнение:
![]() =
= ![]()
| 3) х = 4 | |
| 2) х = - 62 | 4) х = 82 |
-
Решите уравнение:
2 ( х – 3 ) = 3 ( 4 – х ) + 5
| 3) х = - 11 | |
| 2) х = | 4) х = |
Сумма правильных ответов в обоих вариантах равна 11. Выставляются оценки: каждый сам себе.
8. Итог урока.
Учитель: Каким сегодня был для нас урок (закрепление или открытие) и почему?
Предполагаемый ответ ученика: Закрепления. Так как мы отрабатывали свои затруднения по теме.
Учитель: Что нам помогало на уроке?
Предполагаемый ответ ученика: Правила решения уравнений.
Учитель: Оцените свою работу на уроке.
У каждого ученика на столе лежит заготовка
 Если вам все было понятно, то нарисуйте лицо № 1, если что-то осталось еще не понятым – лицо № 2, в остальных случаях - № 3.
Если вам все было понятно, то нарисуйте лицо № 1, если что-то осталось еще не понятым – лицо № 2, в остальных случаях - № 3.
П лакат
лакат
Учитель: Спасибо.
Учитель: Пришло время для нового домашнего задания. Задание дается по выбору.
-
№ 166 (ж, з, е)
-
Если вы захотите узнать, сколько лет прожил Диофант, то № 114.
-
Творческое. Придумать задачу, решение которой бы сводилось к решению уравнения 3 х – 120 = х + 40 и оформить ее решение.
Спасибо за урок.
Здесь представлен конспект к уроку на тему «Решение уравнений», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (6 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.


