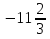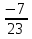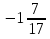Конспект урока «Решение уравнений, сводящихся к линейным» по алгебре для 7 класса
Министерство образования и науки Российской Федерации
Управление образования администрации города Твери
МОУ СОШ № 7
Городской конкурс
педагогических разработок
«Мой лучший урок»
Направление работы разработка урока по алгебре 7 класса
По теме «Решение уравнений, сводящихся к линейным»
Выполнила: Ботнева Мария Юрьевна
Должность: учитель математики
Тверь, 2009
Пояснительная записка:
По данным социологических исследований в российском обществе значительно изменилось отношение к таким непреходящим ценностям, как Отечество, патриотизм, верность героическим традициям, память к павшим за родину, долг, честь, знание истории своего народа и д. р.
Резко сменились акценты в социально-нравственных ориентирах значительной части общества, особенно молодежи: они стали более прагматизированными, конъюнктурными, но и эгоцентричными, даже анти социальными и антигуманными, что выражается в росте преступности среди несовершеннолетних.
Таким образом, в современных условиях социально-культурного развития общества главной задачей школы становится воспитание растущего человека как личности, обладающей высоким нравственным потенциалом, знающей и уважающей традиции своего народа.
Одним из важнейших аспектов своей деятельности я считаю формирование у подрастающего поколения гражданственности, патриотизма, чувства ответственности за судьбу Отечества. Интегрированные уроки, наряду с внеклассной деятельностью, позволяют расширить кругозор учащихся, обращая их к истории родного края, военной истории, истории России.
Данный урок является третьим в теме «Решение уравнений». Учащиеся обладают достаточным комплексом знаний для решения уравнений, а именно: правила раскрытия скобок, правило перенесения слагаемых из одной части уравнения в другую, правило деления обоих частей уравнения на одно и то же число. Урок посвящен развитию практических навыков решения уравнений.
Урок рассчитан на класс со средними и слабыми математическими способностями. Объединение в группы происходит по взаимному выбору. Оценки выставляются по итогам проверки тетрадей.
Тема урока: Решение уравнений, сводящихся к линейным с использованием краеведческого материала.
Тип урока: урок-игра.
Цели:
Дидактическая - закрепить навыки решения уравнений, сводящихся к линейным;
Развивающая – способствовать развитию мышления и речи, внимания и памяти;
Воспитывающая – воспитывать любовь к родному городу.
Задачи:
-
Углубление навыков и умений решения уравнений, сводящихся к линейным, знакомство с историческим материалом.
-
Воспитание исследовательских умений и навыков, выработки умения публично выступать, потребности в творческой самореализации, самообразовании, самосовершенствовании, приобщать обучающихся к общечеловеческим ценностям.
-
Развитие мотивации личности к познанию и творчеству, логического и наглядно-образного мышления учащихся и формированию адекватной самооценки, умений самостоятельно работать, говорить, слушать, способности использовать знания и умения в реальной жизненной практике.
-
Повышение интереса школьников к математике, истории родного края, расширение их кругозора, патриотического воспитания, бережного отношения к историческим памятникам города Твери.
Предварительная работа: отдельные учащиеся готовят материал по теме: «Великие люди Твери».
Структура:
-
Организационный момент.
-
Проверка домашнего задания.
-
Устная работа.
-
Самостоятельная работа.
-
Игровой момент.
-
Домино.
-
Подведение итогов.
-
Домашнее задание.
Ход урока:
I. Организационный момент.
Учащиеся класса делятся на 4 группы. Выбирают название и капитана.
Условия игры: Команда, выполнившая задание первой получает 3 очка; второй – 2…
II. Проверка домашнего задания.
Проводится с помощью таблицы ответов:
| Т. -24 | Д. 24 | С. 75 | |
| О. 2 | В. -2 | Е. -2,5 |
| С. -2 | Н. 8 | Е. 2 |
| Р. -13 | Н. 13 | К. |
| А. 1 | Ь. 7 | И. -1 |
Город древний, родной, купола и аллеи
Чайки гордый полет над простором реки.
Тверь моя, с каждым днем мне дороже, милее
Сердцу очень нужна ты, ты одна, только ты!
Н. Лосева
Учитель:
Каждому человеку нужно знать, какими были и как жили его давние и недавние предки, что довелось испытать и пережить народам нашей Родины на протяжении прошедших веков. Прошлое народа, страны, человечества изучает наука история.
Сегодня у нас необычный урок, он посвящен истории родного края. Вы познакомитесь лишь с отдельными страницами, фрагментами, эпизодами истории, так как обо всем, что произошло, на одном уроке не рассказать.
Надеюсь, что обращение к родной истории не только побудит вас глубже и подробнее изучить прошлое Твери, заняться исследовательской работой, но и заставит внимательнее и бережнее относится к тому, что вас окружает.
Первое поселение на месте нынешнего города возникло на рубеже IX-X веков. Оно находилось на мысу при впадении реки Тьмаки в Волгу. В 1164 году Тверь упоминается в документах как небольшая крепость на западной границе Суздальского княжества.
О происхождении названия города существует несколько версий. Согласно одной из них его нарекли в честь реки Тверцы, а Тверца в свою очередь является производным от финского слова "tiort" - "быстрый". По другой версии, имя города произошло от славянского "твердь", что означает "крепость".
III. Устная работа.
Выполнив следующее задание, вы узнаете имя первого Тверского князя.
-
Какое из чисел является корнем уравнения х+3=2х-9?
10-д 12-я 6-м
-
Для какого из уравнений число 3 является корнем?
х∙0,002=6,023 -и |х|=-3-м (-х)2=9-р
-
Какое из уравнений не имеет корней?
х+х=-100-и х∙х=-100-о х-1000=-1000-х
-
От числа Х отняли 4, полученную разность разделили пополам и получили столько же, как если бы от Х отняли 26. Какое из уравнений соответствует этому условию?
(х-4):2=26-а 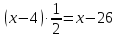 -с
-с 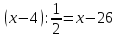 -т
-т
-
Какое из уравнений имеет тот же корень, что и уравнение 2х-5=73?
2х=73-5-р 2х=73+5-л 2х-73=-5-и
-
Корнем, какого из уравнений является любое неотрицательное число?
Х+2=2х-л х=х2 -и |х|=х-а
-
Найдите корень уравнения 2х+54=94
20-в -20-й 74-а
Имя первого Тверского князя - Ярослав Ярославич, хотя более известен его потомок – Михаил Ярославович, пожертвовавший собственной жизнью ради спасения своего народа.
Тверская земля во все времена была богата выдающимися людьми, которые многое сделали как для родного края, так и для России, тем самым навсегда вписав свои имена в историю нашего государства. Сложно переоценить их вклад в развитие культуры, религии, науки, становлении России на различных этапах ее истории. Выполнив работу, вы познакомитесь с некоторыми известными фамилиями, прославившими наш город.
IV. Самостоятельная работа.
-
(13а-7)+8=12а+11
-
(5х-3)+(7х-4)=8-(15-11х)
-
(4х+3)-(10х+11)=7+(13-4х)
-
(3-2х)+(4-3х)+(5-5х)=12+7х
-
6(х-3)=3(15-х)
-
0,6(х-9)=0,2(23-2х)
-
7(х+1)-2(х-4)=х-9
-
3(х-1)-2(х-5)=5х+13
-
2=(3х-5)-(7-4х)
-
Сумма задуманного числа и 11 равна разности 15 и задуманного числа. Какое число задумано?
Ключи:
| 1 команда | 2 команда | 3 команда | 4 команда | |||||||||||||
| 1 | 10 д | -10 н | 26 д | 10 с | 26 п | -10 с | -10 м | 10 л | 26 б | -10 и | 26 ек | 10 ан | ||||
| 2 | 0 у | 2 и |
е |
а | 0 и | 2 у |
о | 0 е | 2 и | 0 др | 2 в |
а | ||||
| 3 | -3 к | -14 н | 14 м | -14 д | -3 л | 14 ш | -14 м | 14 х | -3 р | 14 а | -14 ей | -3 т | ||||
| 4 |
е | 1 и | 0 а |
к | 0 е | 1 т |
и | 3 а | 0 е |
е | 1 н | 0 т | ||||
| 5 | 7 е | 9,6 н | -7 т | 9,6 ы | 7 л | -7 и | 7 ш | -7 и | 9,6 с | -7 к | 9,6 р | 7 у | ||||
| 6 | 4 и | 10 в | -10 т | -4 н | 10 ь | -10 к | 4 п | -10 л | 10 е | -4 и | 10 п | -10 р | ||||
| 7 | -1,5 ь | -6 с | 6 н | -1,5 ов | 6 ал | -6 н | -6 в | 6 к | -1,5 о | -6 о | 6 ы | -1,5 на | ||||
| 8 | 1,5 аф | -6,5 е | -1,5 к | -6,5 ек | -1,5 и | 1,5 ще | -6,5 л | -1,5 С | 1,5 р | 1,5 л | -6,5 вт | -1,5 л | ||||
| 9 | -2 в | 2 и | -14 ана | 2 к | -14 др | -2 са | -2 у | 2 ерг | -14 ев | -14 ор | 2 е | -2 о | ||||
| 10 | 2 й | 13 сий | -2 а | 13 ндр | 2 ов | -2 ин | 2 ей. | -2 г | 13 ой | 13 ая | -2 в | 2 в | ||||

Дунаевский Константин Дмитриевич родился в 1922 г. в городе Ржеве в семье служащего. Он учился в 6-й школе, занимался в аэроклубе, окончил Батайское авиационное училище. На фронте - с 1943 года, мастер воздушной разведки.
Больше ста раз Дунаевский вылетал на разведку глубоких вражеских тылов. Только над Берлином, Данцигом и Гдыней он появлялся по десять раз, над Кенигсбергом - восемь раз. За образцовое выполнение заданий командования он был награжден в июле 1944 года орденом Отечественной войны I степени, в августе - орденом Красного Знамени, в сентябре - вторым орденом Красного Знамени.
Дунаевский погиб в небе над Берлином 23 апреля 1945 года. Звание Героя Советского Союза ему присвоено 18 августа 1945 года.
Андрей Николаевич Туполев родился 10 ноября 1888 года в селе Пустомазово Тверской губернии. Андрей Николаевич родился в многодетной семье. Окончил Тверскую гимназию и успешно сдал экзамены сразу в два института, выбрав из них Московское высшее техническое училище. Слушал лекции Н.Е. Жуковского, занимался в воздухоплавательном кружке и на построенном планере совершил свой первый полет. 
В 1918 г., окончив училище, Туполев вместе с Н.Е. Жуковским стал организатором Центрального аэродинамического института, где возглавил отдел авиации, гидроавиации и опытного строительства. В начале 20-х гг. Туполев возглавлял опытное КБ, где работал над созданием торпедных катеров, аэросаней, дирижаблей, самолетов.
Самолеты конструкторского бюро Туполева показали высокие летные качества во время спасения челюскинцев в 1934 г., перелетов из СССР в США через Северный полюс в 1937 г. и в др. случаях.
Под руководством Туполева было создано свыше 100 типов военных и гражданских самолетов.
Николай Николаевич Сиде́льников (5 июня 1930, Тверь — 1992) — советский российский композитор, заслуженный деятель искусств РСФСР, народный артист РСФСР (1992), Лауреат Государственной премии РСФСР им. М. И. Глинки, профессор Московской консерватории с 1981.
Окончил Московскую Государственную консерваторию в 1957 году по классу композиции Е. И. Месснера, аспирантуру по классу Ю. А. Шапорина; с 1958 года ассистент Шапорина и А. И. Хачатуряна; с 1961 года вёл в Московской консерватории свой класс композиции. Был одним из ведущих профессоров Московской консерватории со своей уникальной методикой преподавания теории и практики композиции. Его школа дала более десятка молодых композиторов с прочно установившимся мировым именем: среди них Вячеслав Артёмов, Эдуард Артемьев (организатор и зачинатель электронной музыки в СССР), Дмитрий Смирнов, Владимир Тарнопольский, Владимир Мартынов, Иван Соколов, Ираида Юсупова и многие другие.

Сергей Яковлевич Лемешев родился в деревне Старое Князево (Тверская губерния) 27 июня 1902 в крестьянской семье. Окончил церковно-приходскую школу и был послан обучаться сапожному делу в Петербург; после окончил общеобразовательную школу в Твери, одновременно посещал уроки в музыкальной школе. В 1921–1925 учился в Московской консерватории в классе Н.Г.Райского; с 1924 работал в Оперной студии под руководством К.С.Станиславского. В 1931 был приглашен в Большой театр, где дебютировал в партиях Царя Берендея (Снегурочка Римского-Корсакова), Ленского (Евгений Онегин Чайковского. До 1956 был ведущим солистом театра, где спел множество партий: Левко (Майская ночь), Звездочет (Золотой петушок), Индийский гость (Садко) в операх Н.А.Римского - Корсакова и др. Партию Ленского – вершину своего репертуара – Лемешев в последний раз исполнил на сцене Большого театра в 1972, когда отмечалось 70-летие певца.
V. Ближе - дальше.
-
Необходимо написать число, максимально приближенное к верному ответу.
-
Команда получает 1 очко за каждый максимально приближенный ответ и 3 очка за правильный ответ.
-
Назовите год рождения Михаила Ярославовича Тверского.
1271 г
-
Назовите длину Старого Волжского моста (в метрах).
215,5 м
-
Назовите год Великого пожара.
1763 г.
-
Назовите год основания Ботанического сада.
1879 г
-
Назовите год сооружения Тверского кремля
1182 г.
-
В каком году закончилось сооружение Путевого Дворца?
1767 г
-
Назовите длину Восточного моста (в метрах).
1900 м
VI. Домино.
В 2010 году у нашего города ЮБИЛЕЙ. А какой именно – вам предстоит выяснить с помощью домино:
| 2010 | 7х+21=х-3 | |
| -4 | - | 8,31к-71=1,11к+1 |
| 10 | 1 | 8у-(7у-142)=51 |
| -91 | 1 | 9-(8х-11)=12 |
| 1 | 3 | 2х+3-(5х+11)=7+(13-2х) |
| -28 | 5 | 11х+13=1+(12х-31) |
| 43 | = | 0,71а-13=10-0,29а |
| 23 | 8 | 2=3у-5-(7-4у) |
| 2 | 7 | 14-5х-(8-4х)+(5х+6)=8 |
| -1 | 5 | |
Нашему городу – 875 лет.
Я славлю Тверь – наш город самый лучший
Зеленый, светлый, словно солнца луч.
Тебе моя любимая столица
От сердца своего вручаю ключ!
VII. Подведение итогов.
VIII. Домашнее задание.
Творческое задание: Приготовить домино по теме «Решение уравнений»
в 8-10 ходов.
Литература:
-
Город Калинин. Издательство «Московский рабочий», 1983г.
-
Тверская земля – Русская Европа. Издательство «Тверское княжество», 2006г.
-
Тверская область. Энциклопедический справочник. Тверское областное книжно-журнальное издательство, 1994г.
-
Поисковое движение в Тверской области – к 60-летию освобождения г. Калинина от немецко-фашистских захватчиков. Администрация Тверской области, 2002г.
-
Сеть интернет:
-
http://www.rossimvolika.ru/sub_RF/tverskaya_obl/gerb/history/
-
http://www.idcity.ru/TverHistory.aspx
Здесь представлен конспект к уроку на тему «Решение уравнений, сводящихся к линейным», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (7 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.