Конспект урока «Квадратные уравнения. Основные понятия. Решение неполных квадратных уравнений» по алгебре для 8 класса
Тема: «Квадратные уравнения. Основные понятия. Решение неполных квадратных уравнений»
Тип урока: урок изучения нового материала.
Цели урока:
- формирование знаний учащихся о способах решения неполных квадратных уравнений в зависимости от вида неполного квадратного уравнения;
- развитие умений сравнивать, выявлять закономерности, обобщать;
- развивать навыки самоконтроля;
- воспитывать волю и настойчивость для достижения конечных результатов при решении неполных квадратных уравнений.
Оборудование:
- таблицы с формулами сокращенного умножения;
- раздаточный материал.
Структура урока:
- организационный момент;
- постановка цели урока;
- ознакомление с новым материалом;
- подведение итогов урока;
- постановка домашнего задания;
Ход урока:
-
Организационный момент.
Поверяется подготовленность классного помещения и готовность учащихся к уроку.
-
Постановка цели урока.
Сегодня на уроке мы продолжим изучение темы «Неполные квадратные уравнения». На предыдущем уроке мы с вами познакомились с видами неполных квадратных уравнений, научились преобразовывать уравнения и приводить к квадратным. Целью сегодняшнего нашего урока будет научиться решать неполные квадратные уравнения. А делать это вы будете с помощью учебных элементов, в которых дается описание способа решения того или иного вида неполного квадратного уравнения, а также задания для самостоятельной работы. Учебные элементы поделены на три уровня:
I-й уровень - содержит обязательный минимум, который должны выполнить все учащиеся. (обеспечивает при правильном выполнении оценку «3»);
II-й уровень – задания представлены в усложненном виде (обеспечивает при правильном выполнении оценку «4»);
III-й уровень - задания представлены в нестандартном виде и требуют большей подготовленности (обеспечивает при правильном выполнении оценку «5»);
Учебные элементы с 1-го по 4-й представляют собой I-й уровень сложности, учебный элемент № 5 - II-й уровень сложности, учебный элемент № 6 - III -й уровень сложности.
Эталоны ответов и критерии оценивания находятся у учителя.
Желаю удачи!
-
Ознакомление с новым материалом.
Каждый учащийся получает учебный элемент, читает указания учителя и выполняет самостоятельную работу. После чего сверяет свои ответы с эталонными и ставит набранное количество баллов в оценочный лист. После того, как учащийся набирает необходимое количество баллов, приступает к выполнению следующего учебного элемента.
-
Подведение итогов.
Учащиеся подводят итоги своей работы, оценивая самостоятельно согласно набранным баллам. Оценки выставляются в журнал.
-
Постановка домашнего задания.
Выполнить следующие задания:
а) устно - прочить § 19 учебника «Алгебра - 8»(А.Г.Мордкович) – пример 1.
б) письменно -
Учебный элемент № 1
Цель: закрепить умения решать уравнения вида х2 = а.
Указания учителя
Вспомните правила решения уравнения х2 = а. Для этого прочитайте пояснения, данные ниже.
Рассмотрим уравнение х2 = а, где а – произвольное число. В зависимости от числа а при решении этого уравнения возможны три случая.
Если а 0, то уравнение х2 = а корней не имеет. Действительно, не существует числа, квадрат которого был бы равен отрицательному числу.
Если а = 0, то уравнение имеет один корень, равный нулю.
Если а 0, то уравнение имеет два корня:х1 = 
и х2 = - .
Выполните письменно самостоятельную работу.
Задания для самостоятельной работы
Вариант I
1) х2 = 81 (1 балл)
2) х2 = 0 (1 балл)
3) х2 = - 36 (1 балл)
Указания учителя
Список правильных ответов и критерии оценивания возьмите у учителя. Исправьте ошибки, если они есть. Число набранных баллов поставьте в графу «Основные задания» оценочного листа. Если вы набрали 3 балла, то переходите к следующему учебному элементу. Если же набрано меньше баллов, то решите задания другого варианта, аналогичные тем, в которых была допущена ошибка. Набранные баллы поставьте в графу «Корректирующие задания».
Учебный элемент № 1
Цель: закрепить умения решать уравнения вида х2 = а.
Указания учителя
Вспомните правила решения уравнения х2 = а. Для этого прочитайте пояснения, данные ниже.
Рассмотрим уравнение х2 = а, где а – произвольное число. В зависимости от числа а при решении этого уравнения возможны три случая.
Если а 0, то уравнение х2 = а корней не имеет. Действительно, не существует числа, квадрат которого был бы равен отрицательному числу.
Если а = 0, то уравнение имеет один корень, равный нулю.
Если а 0, то уравнение имеет два корня:х1 = и х2 = - .
Выполните письменно самостоятельную работу.
Задания для самостоятельной работы
Вариант II
1) х2 = 36 (1 балл)
2) х2 = 0 (1 балл)
3) х2 = - 25 (1 балл)
Указания учителя
Список правильных ответов и критерии оценивания возьмите у учителя. Исправьте ошибки, если они есть. Число набранных баллов поставьте в графу «Основные задания» оценочного листа. Если вы набрали 3 балла, то переходите к следующему учебному элементу. Если же набрано меньше баллов, то решите задания другого варианта, аналогичные тем, в которых была допущена ошибка. Набранные баллы поставьте в графу «Корректирующие задания».
Учебный элемент № 2
Цель: научить учащихся решать уравнения вида ах2 = 0.
Указания учителя
Прочитайте данные ниже пояснения.
Неполные квадратное уравнение вида ах2 = 0, равносильно уравнению х2 = 0 и поэтому имеет единственный корень, равный нулю.
Пример. Решите уравнение 4х2 = 0.
Решение. Так как уравнение вида ах2 = 0, равносильно уравнению х2 = 0, то
4х2 = 0
х2 = 0
х= 0.
Ответ: х = 0.
Выполните письменно самостоятельную работу.
Задания для самостоятельной работы
Вариант II
1) 5х2 = 0 (1 балл)
2) - 8х2 = 0 (1 балл)
3) 
(2 балла)
Указания учителя
Список правильных ответов и критерии оценивания возьмите у учителя. Исправьте ошибки, если они есть. Число набранных баллов поставьте в графу «Основные задания» оценочного листа. Если вы набрали 3 баллов и более, то переходите к следующему учебному элементу. Если же набрано меньше баллов, то решите задания другого варианта, аналогичные тем, в которых была допущена ошибка. Набранные баллы поставьте в графу «Корректирующие задания».
Учебный элемент № 2
Цель: научить учащихся решать уравнения вида ах2 = 0.
Указания учителя
Прочитайте данные ниже пояснения.
Неполные квадратное уравнение вида ах2 = 0, равносильно уравнению х2 = 0 и поэтому имеет единственный корень, равный нулю.
Пример. Решите уравнение 4х2 = 0.
Решение. Так как уравнение вида ах2 = 0, равносильно уравнению х2 = 0, то
4х2 = 0
х2 = 0
х= 0.
Ответ: х = 0.
Выполните письменно самостоятельную работу.
Задания для самостоятельной работы
Вариант I
1) 14х2 = 0 (1 балл)
2) - 7х2 = 0 (1 балл)
3) 
(2 балла)
Указания учителя
Список правильных ответов и критерии оценивания возьмите у учителя. Исправьте ошибки, если они есть. Число набранных баллов поставьте в графу «Основные задания» оценочного листа. Если вы набрали 3 баллов и более, то переходите к следующему учебному элементу. Если же набрано меньше баллов, то решите задания другого варианта, аналогичные тем, в которых была допущена ошибка. Набранные баллы поставьте в графу «Корректирующие задания».
Учебный элемент № 3
Цель: научиться решать уравнения вида ах2 + с = 0, где с
0.
Указания учителя
Прочитайте данные ниже пояснения.
Для решения неполного квадратного уравнения вида ах2 + с = 0, где с0 переносят его свободный член в правую часть и делят обе части уравнения на а. Получают уравнение 
, равносильное уравнению ах2 + с = 0.
Так как с0, то 
Если 
0, то уравнение имеет два корня: 
.
Если 0, то уравнение не имеет корней.
Пример 1. Решите уравнение 4х2 + 3= 0.
Решение. Перенесем свободный член в правую часть уравнения и обе части получившегося уравнения разделим на 4:
4х2 = - 3
х2 = -
.
Так как квадрат числа не может быть отрицательным числом, то получившееся уравнение не имеет корней. А следовательно, не имеет корней и равносильное ему уравнение 4х2 + 3= 0.
Ответ: корней нет.
Выполните письменно самостоятельную работу.
Задания для самостоятельной работы
Вариант I
1) 4х2 – 9 = 0. (2 балла)
2) - 0,1х2 + 10 = 0 (2 балла)
3) 6х2 + 24 = 0. (3 балла)
Указания учителя
Список правильных ответов и критерии оценивания возьмите у учителя. Исправьте ошибки, если они есть. Число набранных баллов поставьте в графу «Основные задания» оценочного листа. Если вы набрали 5 баллов и более, то переходите к следующему учебному элементу. Если же набрано меньше баллов, то решите задания другого варианта, аналогичные тем, в которых была допущена ошибка. Набранные баллы поставьте в графу «Корректирующие задания».
Учебный элемент № 3
Цель: научиться решать уравнения вида ах2 + с = 0, где с0.
Указания учителя
Прочитайте данные ниже пояснения.
Для решения неполного квадратного уравнения вида ах2 + с = 0, где с0 переносят его свободный член в правую часть и делят обе части уравнения на а. Получают уравнение , равносильное уравнению ах2 + с = 0.
Так как с0, то
Если 0, то уравнение имеет два корня: .
Если 0, то уравнение не имеет корней.
Пример 1. Решите уравнение 4х2 + 3= 0.
Решение. Перенесем свободный член в правую часть уравнения и обе части получившегося уравнения разделим на 4:
4х2 = - 3
х2 = -.
Так как квадрат числа не может быть отрицательным числом, то получившееся уравнение не имеет корней. А следовательно, не имеет корней и равносильное ему уравнение 4х2 + 3= 0.
Ответ: корней нет.
Выполните письменно самостоятельную работу.
Задания для самостоятельной работы
Вариант I
1) 2х2 – 18 = 0. (2 балла)
2) - 0,2х2 + 20 = 0 (2 балла)
3) 3х2 + 12 = 0 (3 балла)
Указания учителя
Список правильных ответов и критерии оценивания возьмите у учителя. Исправьте ошибки, если они есть. Число набранных баллов поставьте в графу «Основные задания» оценочного листа. Если вы набрали 5 баллов и более, то переходите к следующему учебному элементу. Если же набрано меньше баллов, то решите задания другого варианта, аналогичные тем, в которых была допущена ошибка. Набранные баллы поставьте в графу «Корректирующие задания».
Учебный элемент № 4
Цель: научить учащихся решать уравнения вида ах2 +вх = 0, где в0.
Указания учителя
Прочитайте данные ниже пояснения.
Для решения неполного квадратного уравнения вида ах2 +вх = 0, где в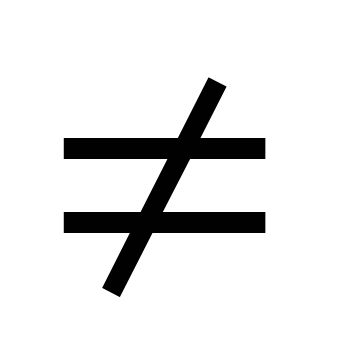0 раскладывают его левую часть на множители и получают уравнение
х ( ах +в) = 0.
Произведение х ( ах +в) равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю:
х = 0 или ( ах +в) = 0.
Решая уравнение ( ах +в) = 0, в котором а0, находим: ах = - в,
х = -
.
Следовательно, произведение х ( ах +в) обращается в нуль при х = 0 и при х = -.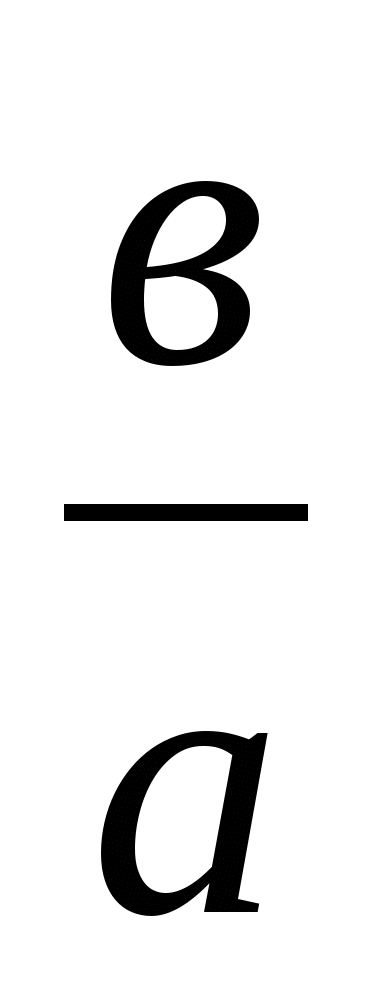
Корнями уравнения х ( ах +в) являются числа 0 и -.
Значит, неполное квадратное уравнение вида ах2 +вх = 0, где в0 всегда имеет два корня.
Пример. Решите уравнение 4х2 + 9х = 0.
Решение. Разложим левую часть уравнения на множители:
х (4х + 9) = 0.
Отсюда х = 0 или 4х + 9 = 0.
Решим уравнение 4х + 9 = 0: 4х = - 9
х = - 
х = - 2
.
Ответ: х1 = 0, х2 = - 2.
Выполните письменно самостоятельную работу.
Задания для самостоятельной работы
Вариант I
1) 3х2 - 4х = 0. (2 балла)
2) -5х2 + 6х = 0. (3 балла)
Указания учителя
Список правильных ответов и критерии оценивания возьмите у учителя. Исправьте ошибки, если они есть. Число набранных баллов поставьте в графу «Основные задания» оценочного листа. Если вы набрали 5 баллов, то переходите к следующему учебному элементу. Если же набрано меньше баллов, то решите задания другого варианта, аналогичные тем, в которых была допущена ошибка. Набранные баллы поставьте в графу «Корректирующие задания».
Учебный элемент № 4
Цель: научить учащихся решать уравнения вида ах2 +вх = 0, где в0.
Указания учителя
Прочитайте данные ниже пояснения.
Для решения неполного квадратного уравнения вида ах2 +вх = 0, где в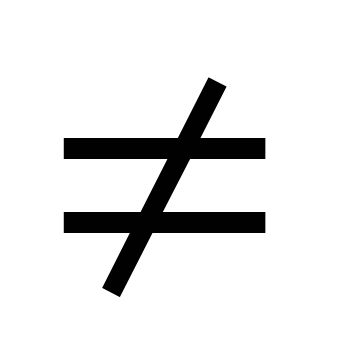0 раскладывают его левую часть на множители и получают уравнение
х ( ах +в) = 0.
Произведение х ( ах +в) равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю:
х = 0 или ( ах +в) = 0.
Решая уравнение ( ах +в) = 0, в котором а0, находим: ах = - в,
х = -.
Следовательно, произведение х ( ах +в) обращается в нуль при х = 0 и при х = -.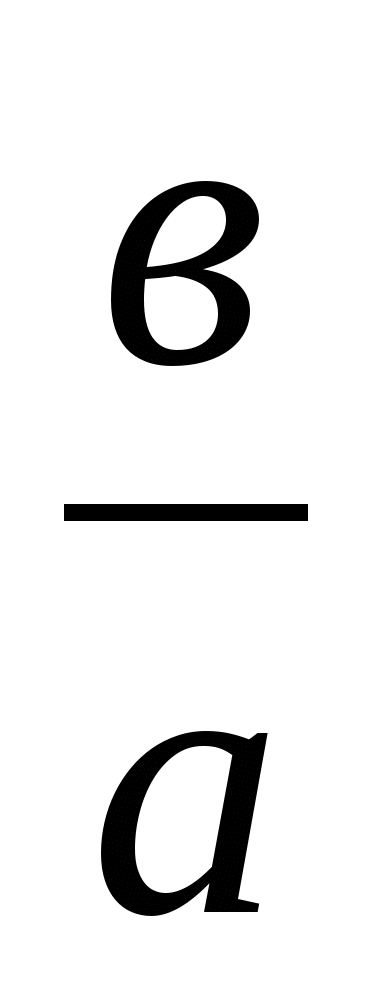
Корнями уравнения х ( ах +в) являются числа 0 и -.
Значит, неполное квадратное уравнение вида ах2 +вх = 0, где в0 всегда имеет два корня.
Пример. Решите уравнение 4х2 + 9х = 0.
Решение. Разложим левую часть уравнения на множители:
х (4х + 9) = 0.
Отсюда х = 0 или 4х + 9 = 0.
Решим уравнение 4х + 9 = 0: 4х = - 9
х = -
х = - 2.
Ответ: х1 = 0, х2 = - 2.
Выполните письменно самостоятельную работу.
Задания для самостоятельной работы
Вариант II
1) 2х2 - 3х = 0. (2 балла)
2) -14х2 + 7х = 0. (3 балла)
Указания учителя
Список правильных ответов и критерии оценивания возьмите у учителя. Исправьте ошибки, если они есть. Число набранных баллов поставьте в графу «Основные задания» оценочного листа. Если вы набрали 5 баллов, то переходите к следующему учебному элементу. Если же набрано меньше баллов, то решите задания другого варианта, аналогичные тем, в которых была допущена ошибка. Набранные баллы поставьте в графу «Корректирующие задания».
Учебный элемент № 5
Цель: - закрепить умения учащихся решать неполные квадратные уравнения;
- проверить умения учащихся выбирать способ решения неполных квадратных уравнений в усложненных заданиях.
Указания учителя
Вы прошли I уровень усвоения материала. Теперь вы самостоятельно выбираете способ решения неполных квадратных уравнений в предложенных заданиях. Для этого вспомните все способы решения неполных квадратных уравнений. Пройденных в 1 - 4 учебных элементах.
Выполните письменно самостоятельную работу.
Задания для самостоятельной работы
Вариант I
1) 2 = 7х2 + 2 (2 балла)
2) 2х2 = 3х (2 балла)
3) 4х2 – 11 = х2 – 11 + 9х (3 балла)
Указания учителя
Список правильных ответов и критерии оценивания возьмите у учителя. Исправьте ошибки, если они есть. Число набранных баллов поставьте в графу «Основные задания» оценочного листа. Если вы набрали 5 баллов и более, то переходите к следующему учебному элементу. Если же набрано меньше баллов, то решите задания другого варианта, аналогичные тем, в которых была допущена ошибка. Набранные баллы поставьте в графу «Корректирующие задания».
Учебный элемент № 5
Цель: - закрепить умения учащихся решать неполные квадратные уравнения;
- проверить умения учащихся выбирать способ решения неполных квадратных уравнений в усложненных заданиях.
Указания учителя
Вы прошли I уровень усвоения материала. Теперь вы самостоятельно выбираете способ решения неполных квадратных уравнений в предложенных заданиях. Для этого вспомните все способы решения неполных квадратных уравнений. Пройденных в 1 - 4 учебных элементах.
Выполните письменно самостоятельную работу.
Задания для самостоятельной работы
Вариант II
1) 9х2 – 1 = -1 (2 балла)
2) 3х2 = -2х (2 балла)
3) 7х2 + 3 = 2х2 + 15х + 3 (3 балла)
Указания учителя
Список правильных ответов и критерии оценивания возьмите у учителя. Исправьте ошибки, если они есть. Число набранных баллов поставьте в графу «Основные задания» оценочного листа. Если вы набрали 5 баллов и более, то переходите к следующему учебному элементу. Если же набрано меньше баллов, то решите задания другого варианта, аналогичные тем, в которых была допущена ошибка. Набранные баллы поставьте в графу «Корректирующие задания».
Учебный элемент № 6
Цель: - проверить знания и умения учащихся решать неполные квадратные уравнения в предложенных заданиях.
Указания учителя
Молодцы! Вы освоили решение неполных квадратных уравнений II уровня сложности Целью дальнейшей вашей работы является применение своих знаний и умений при решении неполных квадратных уравнений в более сложных заданиях.
Выполните письменно самостоятельную работу.
Задания для самостоятельной работы
1) (х - 1)(х + 1) = 2х -1 (2 балла)
2) (х + 3)(х - 4) = -12 (2 балла)
3) (2х -1)2 - 1 = 0 (3 балла)
Указания учителя
В случае затруднений воспользуйтесь подсказками, данными ниже.
-
Воспользуйтесь формулой сокращенного умножения: а2 - в2 = (а - в)(а + в).
-
Перемножьте скобки, приведите подобные слагаемые.
-
Воспользуйтесь формулой сокращенного умножения: (а - в) = а2 – 2ав + в2.
Проверьте и оцените свои работы.
Здесь представлен конспект к уроку на тему «Квадратные уравнения. Основные понятия. Решение неполных квадратных уравнений», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (8 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.
Список похожих конспектов
Графическое решение квадратных уравнений
Управление образования. администрации Павловского района. Проект урока. Предмет алгебра. класс 8 В. Тема. Графическое решение ...
Решение биквадратных уравнений
МУНИЦИПАЛЬНОЕ ОБРАЗОВАНИЕ ТАЗОВСКИЙ РАЙОН. Муниципальное казенное общеобразовательное учреждение. Тазовская школа – интернат среднего (полного) ...
Решение квадратных уравнений
КГУ «Первомайский комплекс «Общеобразовательная средняя школа-детский сад имени Д. М. Карбышева» отдела образования Шемонаихинского района». ...
Решение квадратных уравнений
Муниципальное автономное общеобразовательное учреждение «Средняя общеобразовательная. . школа № 82» г. Перми. Конспект урока алгебры в 8 ...
Решение квадратных уравнений
Урок алгебры с использованием технологии развития критического мышления по теме «Решение квадратных уравнений». Общедидактическая цель:. создание ...
Решение квадратных уравнений
Муниципальное бюджетное общеобразовательное учреждение. «Приютненская средняя общеобразовательная школа №2». Приютненского района Республики Калмыкия. ...
Решение квадратных уравнений
Тема урока Решение квадратных уравнений. Цель урока:. . . - знакомство с методом устного решения квадратных уравнений;. - развивать навыки в ...
Решение квадратных уравнений в среде программирования QBasic 8 класс
Интегрированный урок. Алгебра – информатика. Решение квадратных уравнений в среде программирования QBasic. 8 класс. . Учитель МОУ «СОШ №1 с ...
Решение квадратных уравнений по формуле
" Решение квадратных уравнений по формуле". Тип урока. Урок закрепления знаний. Цели урока. Познавательная:. . - закрепить и систематизировать ...
Решение квадратных уравнений
Урок по теме: "Решение квадратных уравнений". Предмет: Алгебра, урок-обобщение, повторениеТема: Решение квадратных уравнений.Класс: 8 класс. В ...
Логарифмические уравнения решаемые с помощью квадратных уравнений
Министерство образования и науки Республики Казахстан. Атбасарский районный отдел образования. Акмолинской области. Открытый урок по алгебре ...
Решение задач с помощью квадратных и рациональных уравнений
Соснина Галина Кузьминична. учитель математики. МБОУ «СОШ№2» г. Мегион. . Тема: «Решение задач с помощью квадратных и рациональных. . уравнений». ...
Решение задач с помощью квадратных уравнений
Вахнина Татьяна Сергеевна, учитель математики, физики. . Муниципальное общеобразовательное учреждение Перевозовская средняя общеобразовательная ...
Решение квадратных уравнений
Конспект урока по алгебре в 8 классе. Тема урока: «Решение квадратных уравнений». Тип урока. : урок обобщения и систематизации знаний. Цель ...
Решение квадратных уравнений
МБОУ «Чупалейская средняя общеобразовательная школа». Урок: Алгебра 8 класс. Тема:. «Решение квадратных уравнений». Выполнила: Воронина ...
Решение квадратных уравнений
Урок в 8 классе по теме «Решение квадратных уравнений». Учитель :. Спицина Л.А. УМК. : Алгебра. 8 кл.: учеб. для общеобразоват. учреждений / Г.К.Муравин, ...
Решение квадратных уравнений
. План-конспект урока по математике в 8 классе малокомплектной школы. . Тема урока. : Решение квадратных уравнений. Место урока в учебном ...
Решение квадратных уравнений
Захарова Е. А. . Конспект-сценарий урока. Тема:. Решение квадратных уравнений (частные случаи). Цель:. . . - деятельностная: формирование ...
Решение квадратных уравнений
Разработка темы:. Решение квадратных уравнений. Учитель – Тхайшаова Н.Г. Тема: Квадратные уравнения. Способы их решения. . Цель:. ...