Конспект урока «Обобщающий урок. Преобразование выражений, содержащих квадратные корни» по алгебре для 8 класса
Урок алгебры в 8 классе
Тема: Обобщающий урок.
Преобразование выражений, содержащих квадратные корни
Учитель математики: Байтурова А.Р. школа-гимназия №31, г.Астана
2012-2013 учебный год
Цель: повторение понятия квадратного корня, его свойств; развитие умения упрощать выражения, вычислять квадратные корни.
Задачи:
-
закрепить ранее приобретенные знания, умения и навыки учащихся по изучаемой теме;
-
закрепить навыки преобразования выражений, содержащие квадратные корни;
-
способствовать формированию самостоятельного выбора способа решения.
Тип урока: Совершенствование ЗУН учащихся
Методы работы:
- деятельный (процесс познания идет от учеников),
- наглядно – демонстративный,
- частично – поисковый (учим детей наблюдать, анализировать, сравнивать, делать выводы и обобщения под руководством учителя),
- практический
Формы работы: общеклассная, индивидуальная..
Оборудование: интерактивная доска, слайды в PowerPoint., оценочные листы, карточки с тестом, карточки с домашним заданием.
Инновационные технологии:
- компьютерного обучения,
- деятельностного подхода в обучении (познание идет от ученика),
- словесно – продуктивной (на этапе рефлексия),
- личностно – ориентированного обучения (каждый ребенок сможет ответить).
Ход урока.
I. Организационный момент
- Hello, sit down (Здравствуйте, садитесь). Look at the topic of our lesson and tell that it would mean (Посмотрите на тему нашего урока и скажи, что бы это значило).
Правильно, сегодня на уроке мы будем повторять правила преобразования выражений, содержащих квадратные корни, преобразование корней из произведения, дроби и степени, умножение и деление корней, вынесение множителя за знак корня, внесение множителя под знак корня, приведение подобных слагаемых и освобождение от иррациональности в знаменателе дроби. The estimated page will help to sum up a today's lesson (Подвести итоги сегодняшнего урока поможет оценочный лист).
Sign the sheets of paper and answer the first question "Mood at the beginning of a lesson", having chosen one of smilies.(Подпишите свои листы и ответьте на первый вопрос «Настроение в начале урока», выбрав один из смайликов).
II. Сообщение темы урока
Topic of our lesson (Тема нашего урока) «Преобразование выражений, содержащих арифметические квадратные корни». (Слайд №1)
В математике есть нечто,
вызывающее человеческий восторг. Ф. Хаусдорф (Слайд №2)
III. Oral work (Устная работа)
1) Frontal poll (Фронтальный опрос). (Слайд №3)
1.Дайте определение арифметического квадратного корня. (Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а).
2.Перечислите свойства арифметического квадратного корня. (Арифметический квадратный корень из произведения неотрицательных множителей равен произведению корней из этих множителей. Арифметический квадратный корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, делённому на корень из знаменателя).
3.Чему равно значение арифметического квадратного корня из х2? (|х|).
4.Чему равно значение арифметического квадратного корня из х2, если х≥0? х
2) Oral account (Устный счёт) (Слайд №4)
Ну-ка в сторону карандаши!
Ни костяшек. Ни ручек. Ни мела.
"Устный счёт!" Мы творим это дело
Только силой ума и души.
Цифры сходятся где-то во тьме,
И глаза начинают светиться,
И кругом только умные лица.
Потому что считаем в уме!
(Слайд №5-8)
1. Вынесите множитель из-под знака корня: ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() ; 7)
; 7) 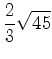 ; 8)
; 8) ![]()
2. Внесите множитель под знак корня: 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() ; 7)
; 7) 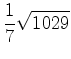 ; 8)
; 8) 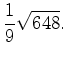
3. Square (Возведите в квадрат): 2, 6, 7, 9, 11, 13,15, 18, 22, 25
4. Приведите подобные слагаемые:
![]()
![]()
![]()
![]()
![]()
IV. Работа по теме урока
1) Individual work (Индивидуальная работа) (Слайд №9)
The green correspond to tasks of a basic level, yellow – to tasks of the raised level, red – to tasks of high level. (Зеленые соответствуют заданиям базового уровня, желтые – заданиям повышенного уровня, красные – заданиям высокого уровня). Учащиеся выбирают задание на свое усмотрение. Трое учащихся, получив задание, решают его в тетрадях
-
уровень
Вынесите множитель из-под знака корня:
1) ![]() 2)
2) ![]() 3)
3) ![]()
Внесите множитель под знак корня:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ;
;
Сравните числа:
1) ![]() и
и![]() ; 2)
; 2) ![]() и
и![]() ;
;
-
уровень
Упростите выражение:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]()
Найдите сумму:
1)![]() 2)
2) ![]()
Раскройте скобки и упростите выражение:
1) ![]() ; 2)
; 2) ![]()
3-уровень
Упростите выражение:
1) 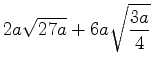 ; 2)
; 2) 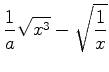 .
.
Преобразуйте выражение:
1) ![]() ; 2)
; 2) ![]() ;
;
Раскройте скобки и упростите выражение:
1) ![]() ;
;
2) ![]() ; 3)
; 3) ![]() ;
;
2) Work with an interactive board (Работа с интерактивной доской). (Слайд №10-13)
Остальные обучающиеся решают следующие задания:
1. Найдите значение выражения:
1) ![]() 2)
2) ![]()
3) ![]()
2. Преобразуйте выражение:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
3. Упростите выражение:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
4. Избавьтесь от иррациональности в знаменателе:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
VI. Historical information (Историческая справка) (Слайд 14-26)
Radix- имеет два значения: сторона и корень. Греческие математики вместо «извлечь корень» говорили «найти сторону квадрата по его данной величине (площади)»
Начиная с XIII века, итальянские и другие европейские математики обозначали корень латинским словом Radix или сокращенно R (отсюда произошёл термин «радикал»).
Немецкие математики XV в. для обозначения квадратного корня пользовались точкой ·5
Позднее вместо точки стали ставить ромбик 5
Затем Ú 5 . Затем знак Ú и черту стали соединять.
VI. Test (Тест)
Английский философ Герберт Спенсер говорил: «Дороги не те знания, которые откладываются в мозгу, как жир, дороги те, которые превращаются в умственные мышцы». (Слайд №27)
At this stage of a lesson it is necessary to apply the knowledge to the solution of exercises during implementation of the test. (На этом этапе урока необходимо применить свои знания к решению упражнений в ходе выполнения теста).
VII. Mutual testing (Взаимопроверка) (Слайд №28)
Код правильных ответов: I вариант – 3124111, II вариант - 2131222
VIII. Homework (Домашнее задание). (Слайд №29)
| С | |
| Какое число меньше B2. Упростите выражение: при B3. Выполнить действия: | Подробные и обоснованные решения заданий этой части напишите аккуратно и разборчиво на листе. С 1. Сократите дробь: С 2. Извлечь квадратный корень из выражения: |
VIII. Итог урока
Заполните до конца оценочный лист. Marks for a lesson (Оценки за урок).
Закончить урок я хочу стихотворением великого математика Софьи Ковалевской. (Слайд №30)
Если в жизни ты хоть на мгновенье
Истину в сердце своем ощутил,
Если луч света сквозь мрак и сомненье
Ярким сияньем твой путь озарил:
Что бы в решенье твоем неизменном
Рок ни назначил тебе впереди,
Память об этом мгновенье священном
Вечно храни, как святыню в груди.
Тучи сберутся громадой нестройной,
Небо покроется черною мглой,
С ясной решимостью, с верой спокойной
Бурю ты встреть и померься с грозой.
В этом стихотворении выражено стремление к знаниям, умение преодолевать все преграды, которые встречаются на пути.
The lesson is ended. Thanks for a lesson! (Урок окончен. Спасибо за урок!) (Слайд №31)
Приложение
ЛИСТ-ОПРОСНИК
Ф.И. ученика____________________________
1. Настроение в начале урока: а) ![]() в)
в) 
2. Мое восприятие темы урока:
а) усвоил(а) все; б) усвоил(а) почти все; в) усвоил(а) частично, нуждаюсь в помощи.
3. Количество неправильных ответов теста: _________
4. Я работал(а) на уроке:
а) отлично; б) хорошо; в) удовлетворительно; г) неудовлетворительно.
5. Я оцениваю свою работу на ______ (поставьте оценку)
6. Я оцениваю урок на _____ (поставьте оценку)
7. Настроение в конце урока:
а)  б)
б)  в)
в) 
| Тест 2 вариант A1. Вычислите 1) 2; 2)6; 3) 4; 4) А 2. Вычислите 1) 2; 2)6; 3) 4; 4) A3. Внесите множитель под знак корня 1) А4.Вынесите множитель из-под знака корня 1) 3 3) 3 А 5. Исключить иррациональность из знаменателя 1) 3) 3 ( А 6. Найдите значение выражения 1) 4; 2) 6; 3) А 7. Упростите выражение 1) |
Здесь представлен конспект к уроку на тему «Обобщающий урок. Преобразование выражений, содержащих квадратные корни», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (8 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

