Конспект урока «Преобразование дробно-рациональных выражений» по алгебре для 8 класса
Интегрированный урок алгебры и информатики.
Тема:
«Преобразование дробно-рациональных выражений. Вставка формул в документ»
Учитель математики
высшей квалификационной категории
Романова И.С.
Тема: Преобразование дробно-рациональных выражений.
Цель: повторить и закрепить свойства действий с дробями и
сформировать способность к их использованию для рационализации
вычислений.
Задачи: 1.Образовательные - повторение и обобщение материала темы,
контроль усвоения знаний и умений.
2.Развивающие – развитие математического и общего кругозора,
мышления и речи, внимания и памяти.
3. Воспитательные – воспитание интереса к математике посредством
использования современных компьютерных
технологий, умения общаться и памяти.
Ход урока: 1. Проверка домашней работы.
2. Фронтальный опрос;
а) Что называется дробью?
( Дробью называется выражение вида а/в, где буквами обозначены числовые выражения или выражения, содержащие переменные. Выражение а называется числителем, а выражение в называется знаменателем дроби.)
Историческая справка: Обозначение дроби в виде а/в впервые встречается в сочинении итальянского учёного Фибоначчи (он же Леонардо Пизанский) в 1202 году. Широкое распространение эта запись получила начиная с XVІ в, после введения так называемой буквенной символики. Тогда же получила распространение и современная форма записи действий с алгебраическими дробями. Основная заслуга в этом принадлежит французскому учёному XVІ в. Франсуа Виету.
Свойства дробей.
-
Основное свойство дроби.
(Если числитель и знаменатель дроби умножить на одно и тоже выражение, то получится тождественно равная ей дробь.)
-
Сложение и вычитание дробей с разными знаменателями.
(Для сложения или вычитания дробей с разными знаменателями дроби приводят к общему знаменателю и затем выполняют преобразования по правилам сложения и вычитания дробей с одинаковыми знаменателями.)
-
Умножение дробей.
(Чтобы выполнить умножение дробей, нужно перемножить их числители и знаменатели отдельно, и первое произведение записать числителем, а второе знаменателем дроби.)
-
Возведение дроби в степень.
(Чтобы возвести дробь в степень, нужно возвести в эту степень числитель и знаменатель дроби, и первый результат записать в числитель, а второй - в знаменатель дроби.)
-
Деление дробей.
(Чтобы разделить дробь на дробь нужно первую дробь умножить на дробь, обратную второй.)
Устная работа:
1. При каких значениях переменной дробь не имеет смысл 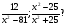
(Дробь не имеет смысла, если знаменатель дроби равен нулю. х≠-9, х≠9, вторая дробь имеет смысл при любых значениях х.)
2. При каких значениях Y значение дроби равно нулю а)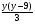 ; б)
; б) 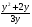 ?
?
(Дробь равна нулю, если числитель дроби равен нулю а) у=0,у=9 б) у=0; у=-2)
3. Сократить дробь а)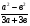 ; б)
; б) ?
?
( а ) 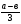 ; б)
; б) 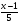 )
)
Практическая часть урока
-
У доски выполняется № 124 (в) (самостоятельно). Затем проектируется решённое задание .Решение
1) 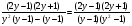
2) 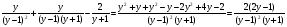
3) 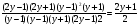
-
С классом выполняется задание:
Построить график функции: у =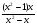
-
Работа по карточкам на местах.
(Проверяется задание , которое выполнялось самостоятельно, карточки собираются и переходим к следующему этапу урока)
-
Любую дробь можно представить в виде суммы двух дробей. Используя данное свойство выполнить задание:
1.Представить дробь 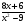 в виде суммы двух дробей.
в виде суммы двух дробей.
У доски самостоятельно выполняется задание:
2. Указать целочисленные значения функции у=
(Преобразуется функция, методом деления многочлена на многочлен, выделяя целую часть, и получается функция вида у=х-2-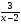
 . Данная функция принимает целочисленные значения, если знаменатель дроби принимает следующие значения (х-2)Є{-3;-1;1;3}, выполняя вычисления находим , что х Є{1;-1;3;5}. Подставляя найденные значения в функцию находим, что у Є{3; -1;-1;3}. Ответ (1;3); (-1;-1);(3;-1) ; (5;3).)
. Данная функция принимает целочисленные значения, если знаменатель дроби принимает следующие значения (х-2)Є{-3;-1;1;3}, выполняя вычисления находим , что х Є{1;-1;3;5}. Подставляя найденные значения в функцию находим, что у Є{3; -1;-1;3}. Ответ (1;3); (-1;-1);(3;-1) ; (5;3).)
На местах некоторые учащиеся выполняют работу по карточкам.
5. Информатика : Вставка формул в документ.
Закон Ома I=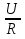
6. Закрепление материала.
Выполняется разноуровневый тест.
Тест (А)

-
Вычислить:
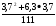
а) 1/3; б)2/3; в)3/4.
2. Найти область определения функции: у = - 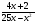
а) х≠-5; х≠0 б) х≠5; х≠0 в) х≠25; х≠0
3. Сократить дробь: 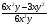
а) 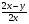 ; б)
; б) 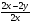 ; в)
; в) 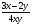
4. Представить в виде дроби выражение: 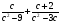
а) 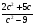 ; б)
; б)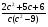 ; в)
; в) 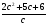
5. Решить уравнение: 
а) 1,5; б) 2,5; в) -1,5
Тест (Б)
1. Вычислить: 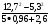
а) 18; б) -20; в) 36
2. Представить дробь в виде суммы двух дробей: 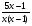 а)
а) 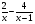 ; б)
; б) 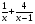 ; в)
; в) 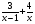
3. Сократить дробь: 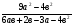
а) 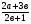 ; б)
; б) 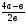 ; в)
; в) 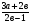
4. Найти целые значения функции: у = 2n -3 + 
а) -4; -1;0;1;3;4;5;8. б) -3;1;0;4;6. в) 8;6;4;0;-1;-2
5.Решить уравнение: 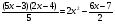
а) 0,5; б)-0,5; в) 2
Разноуровневое домашнее задание. (А) 134 (а,г), 141 (а,в), 144 (Б) 161 (г), 163, 164
7. Занимательная математика

Карточка №1 . Упростить выражение : ( 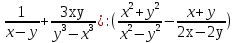
Карточка №2 . Упростить выражение : (2х+1-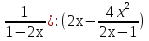
Карточка №3 . Упростить выражение : (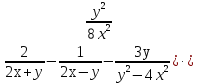 -
-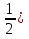
Карточка №1 . Найти значения а и в 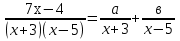
Карточка №2 . Найти целочисленные значения дроби: 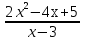
Карточка №3 . Найти целочисленные значения дроби: 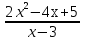
Список использованной литературы:
1. Макарычев Ю.Н, Феоктистов И.Е.. Алгебра.8 класс.- М.:«Мнемозина»,2010
2.Макарычев Ю.Н. Уроки алгебры в 8 классе.- М.:«Просвещение»,2010
3. Феоктистов И.Е... Дидактические материалы для 8 класса..-М.:
« Мнемозина»,2010
-
Семенко Е.А. Технология разноуровневого обобщающего повторения по математике .- «Просвещение -Юг»,2008 год
Здесь представлен конспект к уроку на тему «Преобразование дробно-рациональных выражений», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (8 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

