Конспект урока «Преобразование тригонометрических выражений» по алгебре для 9 класса
Здоровец Людмила Александровна учитель математики высшей категории.
Государственное учреждение «Средняя школа №5».
150009, Северо-Казахстанская область, г. Петропавловск, ул Мира 195,
р.т. 51-85-03, д.т. 42-11-59

Тема: «Преобразование тригонометрических выражений»
9 класс
Цель: обобщение, систематизация и углубление знаний по теме «Преобразование тригонометрических выражений»
Задачи образования: систематизировать знания по данной теме, формировать культуру тригонометрических тождественных преобразований. Работать над преодолением ошибок средствами и содержанием.
Задачи развития: формировать познавательный интерес средствами организации самостоятельной работы, развивать навыки самоконтроля, культуру делового общения.
Задачи воспитания: способствовать эстетическому воспитанию, формируя понимание математических рассуждений, доброжелательность, уважение к мнению других.
Ход урока
-
Организационный момент
-
Этап всесторонней проверки знаний
1. Работа устно:
1) Вычислить: а) tg100∙ tg200∙ tg300∙ tg400∙… tg800
б) cos(-11![]()
в) sin150
г) sin150 ∙ sin750
д) ![]()
2) Дано: tg2ɑ = 4
Вычислить: cos4a
3) Упростить выражения
а) ![]()
б) (sina)-1 + (tga)-1
в) ![]()
г) 2sin2(![]() )-sina
)-sina
4) Найти наибольшее и наименьшее значение выражения:
а) 3 + 2 cosa
б) -|sina|
в) sina - ![]() cosa
cosa
г) 2sinβ + 5cosβ
2. Тест (одного уровня)
-
Упростить:
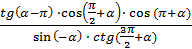
-
Упростить:
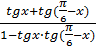
-
Найти наибольшее и наименьшее значение выражения |cos
 | +1
| +1 -
Чему равно выражение
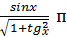 осле упрощения?
осле упрощения? -
Упростить: sin(
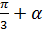 ) - sin(
) - sin(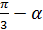 )
) -
Вычислить: 2cos
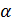 + 4sin2α +
+ 4sin2α + 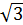 ctg
ctg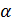 , если tgα =
, если tgα = 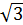 0‹α‹
0‹α‹ .
. -
Упростить: (sinα + cosα)2 + 1 – sin2α
Далее идет взаимопроверка выполненного теста (ученики оценивают друг друга).
1 ученик работает у доски: (уровень В)
Вычислить: а) cos![]()
б) 8sin100 ∙ sin500 ∙ sin700
1 ученик работает с консультантом: (уровень А)
Упростить выражения:
а) ![]()
б) ![]()
в) cos(600 + α) ∙ cos(600 - α) + sin2α
Консультант после выполнения работы анализирует ответ ученика и оценивает его.
Два ученика уровня А выполняют это же задание и сдают на проверку работу. Три ученика уровня В работают в группе со следующим заданием:
-
Дано: tgα =
 ‹ α‹
‹ α‹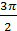
Найти: sin 2α
-
Дано: tgα =
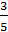
Вычислить: ![]()
-
Дано: cos2α =
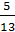
Вычислить: sin4α + cos4α
-
Дано: cosα =
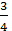
Вычислить: 16sin![]() ∙ sin
∙ sin![]()
Затем класс слушает защиту данной работы (с точностью до идеи).
На протяжении урока ученики заполняют листы самоконтроля.
Класс решает задание у доски, рассматривая два способа решения.
sin2![]() + 2β) – sin2
+ 2β) – sin2![]() - 2β)
- 2β)
I способ. sin2![]() + 2β) – sin2
+ 2β) – sin2![]() - 2β)= (sin
- 2β)= (sin![]() + 2β) – sin
+ 2β) – sin![]() - 2β)) ·(sin
- 2β)) ·(sin![]() + 2β) + sin
+ 2β) + sin![]() - 2β)) = 2sin2β · cos
- 2β)) = 2sin2β · cos![]() · 2sin
· 2sin![]() · cos2 β = sin4β·sinα
· cos2 β = sin4β·sinα
II способ. sin2![]() + 2β) – sin2
+ 2β) – sin2![]() - 2β) =
- 2β) = ![]() =
= ![]() =
= ![]() = sinα · sin4β
= sinα · sin4β
-
Рефлексивно-оценочный этап
Ученики заканчивают заполнение листов самоконтроля и сдают учителю. Учитель анализирует их.
-
Этап информации учащихся о домашнем задании
Домашнее задание.
А. 1. Вычислить:
а) 2sin2α + ![]() cosα + tgα, если ctgα =1 0
cosα + tgα, если ctgα =1 0![]()
б) sin100 ∙ sin500 ∙ sin700
2. Упростить:
а) ![]()
б) 1 +![]()
3. Преобразуйте в произведения:
cos2α – cos3α – cos4α + cos5α
B. 1. Вычислить:
a) ![]() , если tgα = 3
, если tgα = 3
б) sin150 ∙ cos70 - сos110 ∙ cos790
2. Упростить:
a) sin2(α -![]() (1 - tg²α)·tg(
(1 - tg²α)·tg(![]() + α)·cos-2(
+ α)·cos-2(![]() - α)
- α)
б) ![]()
3. Преобразуйте в произведения:
![]()
И напоследок, притча.
«Однажды царь решил выбрать из своих придворных первого помощника. Он подвел всех к огромному дверному замку: «Кто откроет, тот и будет моим первым помощником». Никто не притронулся даже к замку. Лишь один визирь подошел и толкнул замок, который открылся. Он не был закрыт на ключ.
Тогда царь сказал: «Ты получишь эту должность, потому что полагаешься не только на то, что видишь и слышишь, но надеешься на собственные силы, и не боишься сделать попытку».
Лист самоконтроля
Тема: «Преобразование тригонометрических выражений»
Фамилия, имя:
I. Зачет по теоретическому материалу
II. Тест
III. Оценка за выполнение задания
Оцените степень сложности урока.
Вам было на уроке:
-
Легко
-
Обычно
-
Трудно
Оцените степень Вашего усвоения материала:
-
Усвоил полностью, могу применять;
-
Усвоил полностью, но затрудняюсь применять;
-
Усвоил частично;
-
Не усвоил, нужна консультация.
Здесь представлен конспект к уроку на тему «Преобразование тригонометрических выражений», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (9 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

