Конспект урока «Преобразование графиков тригонометрических функций» по алгебре для 10 класса

Конспект урока по алгебре в 10 классе

Васильева Екатерина Сергеевна,

учитель математики

ОГБОУ «Смоленская специальная (коррекционная)

общеобразовательная школа I и II видов»

Смоленск

Тема урока: «Преобразование графиков тригонометрических функций».

Название модуля: преобразование графиков тригонометрических функций.

Интегрирующая дидактическая цель: отработать навыки построения графиков тригонометрических функций.

Целевой план действий для учащихся:

• повторить основные свойства тригонометрических функций;

• отработать навык преобразования графиков тригонометрических функций;

• способствовать развитию логического мышления;

• воспитывать интерес к изучению предмета.

Банк информации.

Входной контроль.

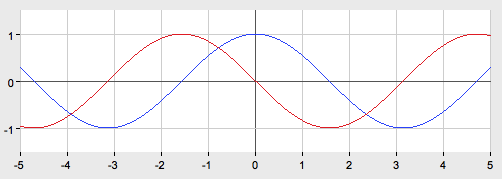
Назовите свойства функций y = sin x (рис. 1).

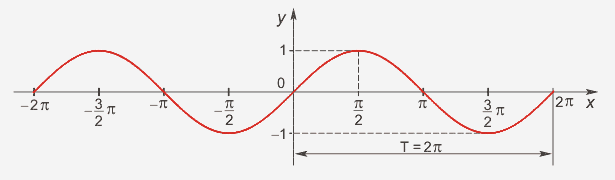
Рис. 1

Свойства:

1. D(y)=R

2. E(y)=[-1;1], функция ограничена

3. sin(-x)=-sinx, функция нечётная

4. Наименьший положительный период: 2π
   sin (x+2πn)= sin x, n Є Z, x Є R.

5. sin x=0 при x=πk, kЄ Z

6. sin x>0, x Є (2πk;2π+2πk), k Є Z

7. sin x

8. Наибольшее значение, равное 1, y=sin x принимает в точках x=π/2+ 2πk, k Є Z.

9. Наименьшее значение, равное -1, y=sin x принимает в точках x=3π/2+ 2πk, k Є Z.

Рассмотрим график фукции y= cos x (рис. 2).

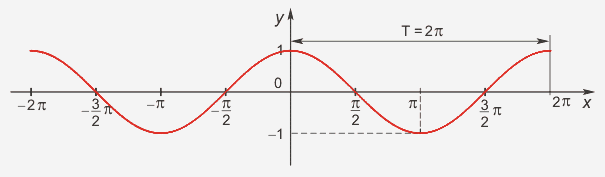
Рис. 2

Свойства:

1. D (y)=R

2. E (y)=[-1;1], функция ограничена

3. cos(-x)= cos x, функция чётная

4. Наименьший положительный период: 2π
   cos (x+2πn)=cos x, n Є Z, x Є R

5. cos x=0 при x=π/2+πk, kЄZ

6. cos x>0, x Є (-π/2+2πk; π/2+2πk), k Є Z

7. cos x

8. Наибольшее значение, равное 1, y=cos x принимает в точках x= 2πk, k Є Z.

9. Наименьшее значение, равное -1, y=cos x принимает в точках x=π+ 2πk, k Є Z.

Cледующий график функции y=tg x (рис. 3)

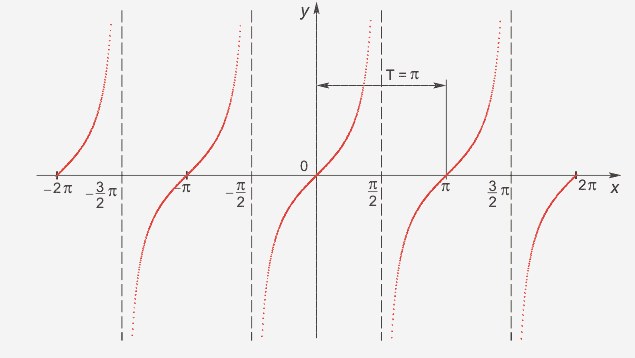
Риc. 3

Свойства:

1. D(y)-множество всех действительных чисел, кроме чисел вида x=π/2 +πk, k Є Z

2. E(y)=(-∞;+ ∞), функция неограниченная

3. tg(-x)=-tg x, функция нечётная

4. наименьший положительный период: π
   tg(x+π)= tg x

5. tgx= 0 при x=πk, k Є Z

6. tg x> 0, x Є ( πk; π/2+πk), k Є Z

7. tg x

Следующий график функции y=ctg x (рис. 4)

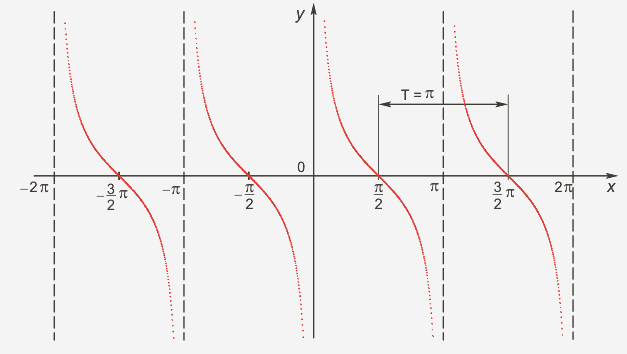
Рис. 4

Свойства:

1. D(y)-множество всех действительных чисел, кроме чисел вида x=πk, k Є Z

2. E(y)= (-∞;+ ∞), функция неограниченная

3. ctg(-x)=-ctg x, функция нечётная

4. Наименьший положительный период: π
   ctg(x+π)=tg x

5. ctg x = 0 при x=π/2+πk, k Є Z

6. ctg x>0, x Є( πk; π/2+πk), k Є Z

7. ctg x

Объяснение материала.

1. Для построения графика функции y=f(x)+a, где a - постоянное число, надо перенести график y=f(x) вдоль оси ординат. Если a>0, то график переносим параллельно самому себе вверх, если a

2. Для построения графика функции y=kf(x) надо растянуть график функции y=f(x) в k раз вдоль оси ординат. Если |k|>1, то происходит растяжение графика вдоль оси OY, если 0k|, то – сжатие.

3. График функции y=f(x+b) получается из графика y=f(x) путем параллельного переноса вдоль оси абсцисс. Если b>0 , то график перемещается влево, если b

4. Для построения графика функции y=f(kx) надо растянуть график y=f(x) вдоль оси абсцисс. Если |k|>1, то происходит сжатие графика вдоль оси OХ, если 0

Закрепление материала.

Уровень А

Частная дидактическая цель: отработать навык построения тригонометрических функций путем преобразований.

Методический комментарий для учащихся: постройте графики функций, выполнив преобразования.

1.

График функции получается из графика путем растяжения вдоль оси Ox в 3 раза.

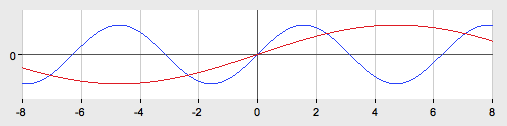
2.

График функции получается из графика путем растяжения вдоль оси Oy в 2 раза.

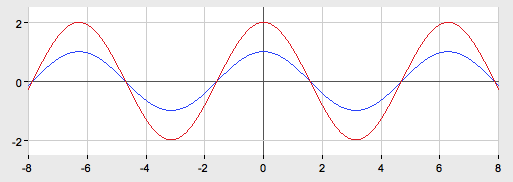
3.

График функции получается из графика путем параллельного переноса на 2 единицы вверх вдоль оси Oy.

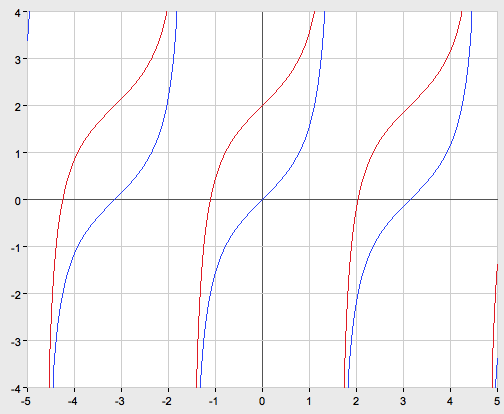
График функции получается из графика путем параллельного переноса вдоль оси абсцисс на единиц влево.

Г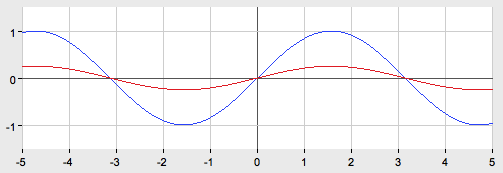
рафик функции получается из графика путем сжатия вдоль оси Oy в 4 раза.

Уровень В.

Частная дидактическая цель: отработать навык построения графиков тригонометрических функций путем последовательного применения преобразований.

Методический комментарий для учащихся: постройте графики функций, выполнив преобразования.

График функции получается из графика путем параллельного переноса вдоль оси абсцисс на единиц вправо.

График функции получается из графика функции путем последовательного выполнения следующих преобразований:

1) параллельный перенос на единицы влево вдоль оси абсцисс

2) сжатие вдоль оси Оy в 4 раза.

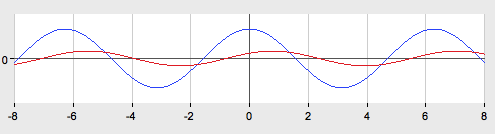
3.

График функции получается из графика функции , каждая ордината которого изменяется в -2 раза. Для этого выполняем следующие преобразования:

1) отображаем симметрично относительно оси Ox,

2) растягиваем в 2 раза вдоль оси Oy.

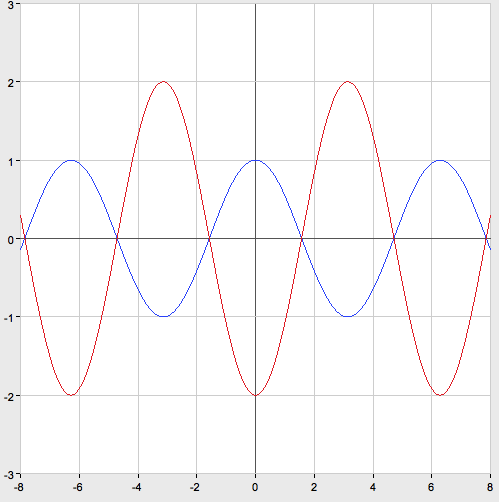
4.

График функции получается из графика функции последовательного выполнения следующих преобразований:

1) сжатие вдоль оси абсцисс в 2 раза;

2) растяжение в 3 раза вдоль оси Oy;

3) параллельный перенос на 1 единицу вверх вдоль оси ординат.

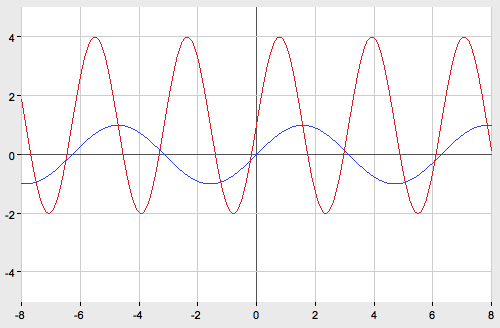
Уровень С.

Частная дидактическая цель: отработать навык построения графиков тригонометрических функций путем последовательного применения преобразований.

Методический комментарий для учащихся: укажите, какие преобразования нужно выполнить для построения графиков. Постройте графики.

1.

График функции получается из графика функциипутем последовательного выполнения следующих преобразований:

1) отображение симметрично относительно оси Ox,

2) сжатие в 2 раза вдоль оси Oy;

3) параллельный перенос на 2 единицы вниз вдоль оси Оy.

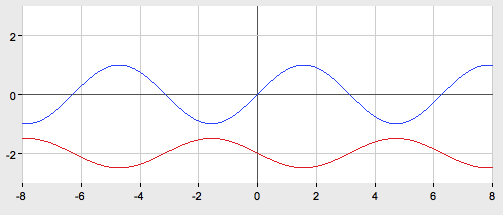
2.

График функции получается из графика функции последовательного выполнения следующих преобразований:

1) параллельный перенос вдоль оси абсцисс на единиц влево,

2) растяжение в 5 раза вдоль оси Oy.

3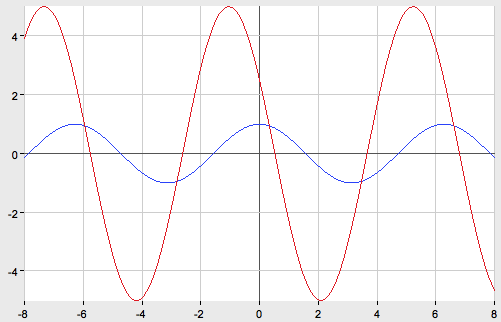
.

График функции получается из графика функции последовательного выполнения следующих преобразований:

1) растяжение вдоль оси абсцисс в 2 раза;

2) параллельный перенос на единиц влево вдоль оси абсцисс.

3) растяжение в 2 раза вдоль оси Oy.

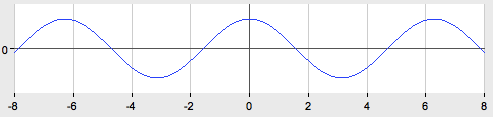
4.

Так как cos (-x)=cos x, следовательно, y= cos x - чётная функция, значит, график функции тот же, что и график функции y= cos x.

5.

График функции получается из графика функции .Части графика функции , расположенные ниже оси абсцисс, зеркально отразятся и будут распо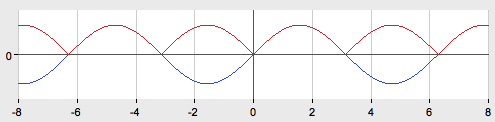
ложены в верхней полуплоскости.

Использованные ресурсы:

http://tvsh2004.narod.ru/alg07.html

http://www.aiportal.ru/services/graph.html