Конспект урока «Свойства тригонометрических функций» по алгебре для 9 класса
 Тема: Свойства тригонометрических функций.
Тема: Свойства тригонометрических функций.
Цель:
Повторить, закрепить, обобщить свойства тригонометрических функций.
Совершенствовать умения и навыки учащихся перевода градусной меры угла в радианную , и наоборот, определения знаков синуса, косинуса, тангенса и котангенса, четности и нечетности, периодичности тригонометрических функций.
Развивать внимание, память, логическое мышление, интерес к предмету.
Воспитывать самостоятельность, ответственность, чувство сотрудничества и взаимопомощи.
1. Организационный этап.
Сообщение темы урока, цели урока.
2. Актуализация знаний учащихся.
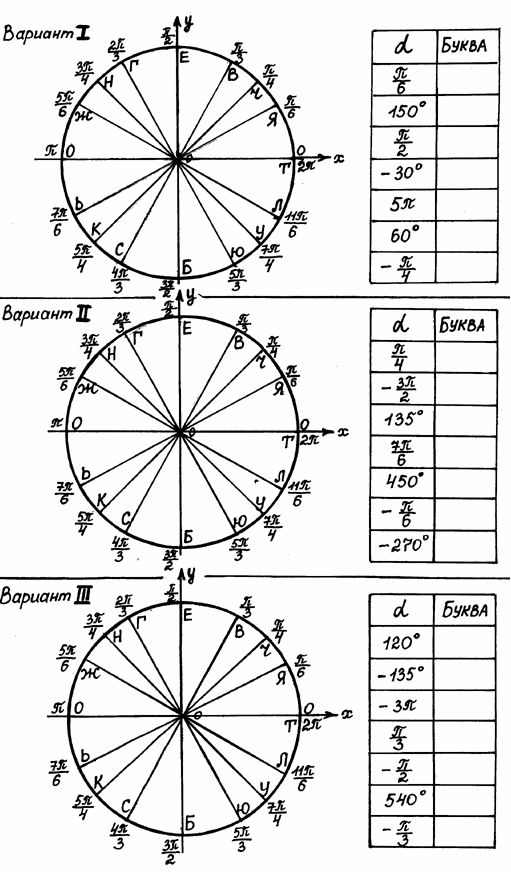
- Повторение. Задания на перевод градусной меры угла в радианную и наоборот, радианную меру угла в градусную.
«Закодированный ответ». Приложение 1.
Задания в 3 вариантах (работа в парах).
Ответ: Тяжело в ученье, легко в бою.
Возьмем эти слова за девиз урока.
- Математический диктант. Приложение 2.
«Закончить предложение» (индивидуальная работа)
Задания на определение четной (нечетной), периодической функции.
Учащиеся выполняют задания под копирку, затем отрывают один лист (оставляют себе), другой передают учителю.
Затем идет фронтальная проверка и выставление баллов (оценивание).
3. Закрепление свойств тригонометрических функций.
Даются дифференцированные задания (уровни А, В, С). Приложение 3.
Уровень А – оценка «3», уровень А + В – оценка «4», Уровень А + В + С – оценка «5».
Затем идет взаимопроверка и оценивание результатов.
Слабым учащимся дается алгоритм решения заданий. Приложение 4.
4. Самостоятельная работа (2 варианта). Приложение 5.
Работа проверяется учителем. (Тетради собираются для проверки)
5. Итог урока.
Анализ допущенных ошибок.
6. Домашнее задание.
Обменяться вариантами самостоятельной работы.
Приложение 1.
Приложение 2.
-
Если выполняется равенство f(-x) = f(x), то функция называется ____________
-
Если выполняется равенство f(-x) = - f(x), то функция называется ____________
-
Если выполняется равенство f(x + Т) = f(x), то функция называется ____________
-
Период функции y = cos x равен__________________.
-
Период функции y = tg x равен__________________.
-
Период функции y = sin x равен__________________.
-
Период функции y = сtg x_равен________________.
-
Функция y = tg x является_________________.
-
Функция y =сtg x является_________________.
-
Функция у = cos x является_________________.
-
Функция у = sinх в 1 четверти имеет знак_________________.
-
Функция у = tgх в 3 четверти имеет знак_________________.
-
Какой знак имеет соs234°_________________.
-
Какой знак имеет tg(-123º)_____________.
-
Какой знак имеет ctg7º _____________.
Подсчет баллов на этом этапе следующий: если верно
Меньше 3 ответов – 0 баллов
От 4 до 6 ответов - 1балл
от 7до 9 ответов – 2 балла,
от 10 до 12ответов – 3 балла,
от 13 до 15 ответов - 4 балла.
Приложение 3.
А
-
Какой знак имеет выражение:
а) sin88°; б) tg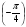 .
.
2. Определить четность (нечетность) функций:
f(x) = cos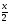 .
.
-
Найти наименьший положительный период функции:
f(x) = ctg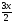 .
.
В
1.Какой знак имеет выражение:
а) sin140°·cos14°; б) 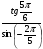 .
.
2. Определить четность (нечетность) функций:
f(x) = х2·ctgx.
C
Найти наименьший положительный период функции:
f(x) = cos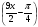 .
.
Приложение 4.
1 свойство. Знаки синуса, косинуса, тангенса и котангенса.
Например: Определить знак выражения: sin14°
Решение: угол в 14° находится в 1-й четверти, значит sin14°> 0.
2 свойство. Четность и нечетность тригонометрических функций.
Функция называется четной, если выполняется равенство f(-x) = f(x)
Функция называется нечетной, если выполняется равенство f(-x) = -f(x)
у = cosx – четная функция, т.е. выполняется равенство cos(-x) = cosx
у = sinx, y = tgx и y = ctgx – нечетные функции, т.е. выполняется равенство
sin(-x) = - sinx; tg(-x) = - tgx; сtg(-x) = - сtgx
Например: Определить четность (нечетность) выражения: у = х + sinx
Решение: у(х) = х + sinx (1)
у(-х) = -х + sin(-x) = - х – sinx (2)
(1) и (2) отличаются знаками, т.е. у(-х) = - у(х), значит функция у(х) = х + sinx
является четной.
3 свойство. Периодичность тригонометрических функций.
Функция называется периодической, если выполняется равенство
f(x + Т) = f(x), где число Т – период функции.
Функции у = cosx и у=sinx имеют период Т = 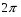 , т.е cos(x +
, т.е cos(x +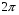 ) = cosx
) = cosx
Функции у = tgx и у=ctgx имеют период Т =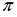 , т.е tg(x +
, т.е tg(x + ) = tgx
) = tgx
Например. Найти наименьший положительный период функции у = tg3x.
Решение. у(х) = tg3x
у(х + Т) = tg3(x + Т) = tg(3х + 3Т). Период для функции у = tgх равен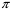 .
.
Значит 3Т = 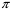 . Отсюда Т =
. Отсюда Т = 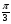 .
.
Приложение 5.
1 вариант
Самостоятельная работа
1. Какой знак имеет:
sin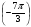
2. Определить четность (нечетность) функций:
а) у = х + 2сtgх
3. Вычислить:
сos(-405°)
2 вариант
Самостоятельная работа
1. Какой знак имеет:
tg(-129°)
2. Определить четность (нечетность) функций:
а) у = cosx – х2
3. Вычислить:
sin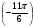
Здесь представлен конспект к уроку на тему «Свойства тригонометрических функций», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (9 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

