Конспект урока «Логарифмы. Свойства логарифмов» по алгебре

 Филиал боу СПО «ЧЕБОКСАРСКИЙ МЕДИЦИНСКИЙ КОЛЛЕДЖ» минздравсоцразвития чувашии Г. КАНАШ чувашской республики
Филиал боу СПО «ЧЕБОКСАРСКИЙ МЕДИЦИНСКИЙ КОЛЛЕДЖ» минздравсоцразвития чувашии Г. КАНАШ чувашской республики
«Утверждаю»
зав учебной части
Филиал
БОУ СПО «ЧМК»
г. Канаш
_______Фадеева Т.Э
«____» ________2014 г.
Методическая разработка
Модуля занятия по дисциплине ОДП.06 Математика
«Логарифмическая функция»
Для специальности:
060501 «Сестринское дело»
Разработала преподаватель
математики и физики
Cеменова А.М
Рассмотрена
на заседании ЦМК ОГСЭ
дисциплин
протокол №____
«____» _______2014 г
Председатель ЦМК
_________ Романова Л.В
Пояснительная записка
Методическая разработка модуля занятия по дисциплине «Математика» на тему «Логарифмическая функция» из раздела «Показательная и логарифмическая функции» составлена на основе Рабочей программы по математике и календарно-тематического плана. Темы занятия взаимосвязаны содержанием, основными положениями.
Программный материал данного занятия базируется на знаниях математики. Рассматриваются вопросы: - Логарифм. Свойства логарифмов.
- Десятичные и натуральные логарифмы.
- Логарифмическая функция свойства и график.
- Логарифмические уравнения и неравенства и методы их решения.
Методическая разработка модуля занятия составлена для проведения теоретических занятий по теме: «Логарифм. Свойства логарифмов» - 2 часа, «Десятичные и натуральные логарифмы» - 2 часа, «Логарифмическая функция, свойства и график» -2 часа, для проведения практических занятий: «Свойства логарифмов» -2 часа, «Логарифмические уравнения» -2 часа, «Логарифмические неравенства» -2 часа по математике для студентов 1 года обучения.
Аннотация
Методическая разработка модуля занятия по теме «Логарифмическая функция» включает программный теоретический и практический материал раздела «Показательной и логарифмической функции», материал для изучения свойств логарифмов, решения уравнений и неравенств студентами и оценка их знаний, вопросы и упражнения для закрепления теоретического занятия.
Методическая разработка модуля занятия по теме «Логарифмическая функция» рекомендуется к использованию преподавателям математики и студентам 1 года обучения.
Филиал БОУ СПО «Чебоксарский медицинский колледж» в г. Канаш
План теоретического занятия.
Специальность: 060501 Дисциплина ОДБ. 06 Математика
Тема: «Логарифмы. Свойства логарифмов»
Тип занятия: Урок усвоения навыков и умений, комбинированное занятие – с элементами беседы и выполнением упражнений.
Цели занятия:
Образовательные - формирование знаний в усвоении понятия логарифма, свойства логарифмов; применять их при решении заданий.
Развивающие - развитие мыслительных операций посредством конкретизации, развитие зрительной памяти, потребности к самообразованию, способствовать развитию познавательных процессов.
Воспитательные - воспитание познавательной активности, чувства ответственности, уважения друг к другу, взаимопонимания, уверенности в себе; воспитание культуры общения. Воспитывать сознательное отношение к учебе и заинтересованность
Средства обучения:
- Методическая разработка по теме.
- Электронная презентация по теме.
- Персональный компьютер, медиапроектор.
- Электронное приложение к учебнику Ш.А Алимов. Издательство «Просвещение».
Внутрипредметные связи: показательная функция и логарифмическая функция.
Межпредметные связи: алгебра и матанализ.
Студент должен знать:
- Обозначение определение логарифма числа, основное логарифмическое тождество.
- три основных свойства логарифма.
Студент должен уметь:
- выполнять преобразования выражений, содержащих логарифмы.
- находить логарифм числа, применять свойства логарифмов при логарифмировании.
- строить график логарифмической функции.
План занятия
1.Организационный момент – 2 мин.
2.Вводная мотивация: постановка целей, изложение плана урока – 3 мин.
3.Проверка домашнего задания – 10 мин.
4.Изучение нового материала - 45 мин.
Основной материал, с использованием электронной презентацией по теме: «Логарифм. Свойства логарифмов»
5.Закрепление материала: Решение задач № 266-271 на стр 90-92. – 25 мин.
6.Подведение итогов – 3 мин.
7. Домашнее задание – 2 мин. § 16 Упражнение № 266-271 четные.
Ход урока:
1. Организационный момент .
2. Вводная мотивация: постановка целей, изложение плана урока.
3. Проверка домашнего задания: Письменно на доске решить № 260-264 (четные).
4. Изучение нового материала: разборка задач 1-5.
Опр: Логарифмом положительного числа b по основанию a, где a > 0, a ≠ 1, называется показатель степени, в которую надо возвести число a, чтобы получить b.
Определение логарифма можно кратко записать так: ![]()
Это равенство справедливо при b > 0, a > 0, a ≠ 1. Его обычно называют логарифмическим тождеством. Действие нахождения логарифма числа называют логарифмированием.
Свойства логарифмов:
![]()
Логарифм произведения:
![]()
Логарифм частного от деления:
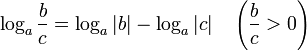
Замена основания логарифма:
![]()
Логарифм степени:
![]()
Логарифм корня:
![]()
Логарифм со степенным основанием:
![]()
![]()
![]()
![]()
![]()
5. Закрепление изученного материала: Решаем № 266—271 нечетные.
Вычислите:
1)log 6 18 + log 6 2 = log 6 36 = 2
2)log12 48 – log 12 4 = log 12 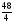 = log 12 12 = 1
= log 12 12 = 1
3)log 3 3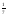 =
= 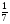 log 33 =
log 33 = 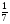
№266
-
log2 16 = 4
-
log 2 2 =1
№ 267
-
log327 = 3
3) log 33 = 1
№ 268
-
log
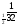 =5
=5
3) log 0.5 0.125 = 3.
№ 269
-
log5 625 = 4
3)log 4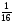 = - 2.
= - 2.
№ 270
-
(
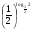 )6 = 26 = 64
)6 = 26 = 64
3)(0,3log0,36)2 = 62 = 36.
6.Подведение итогов.
7.Домашнее задание № 266-271 (четные)
План теоретического занятия.
Специальность: 060501 Дисциплина ОДБ. 06 Математика
Тема : «Логарифмическая функция. Свойства и график»
Тип занятия: Урок усвоения навыков и умений, комбинированное занятие – с элементами беседы и выполнением упражнений.
Цели занятия:
Образовательные - формирование знаний в усвоении понятия логарифмической функции, свойства этой функции и график.
Развивающие - развитие мыслительных операций посредством конкретизации, развитие зрительной памяти, потребности к самообразованию, способствовать развитию познавательных процессов.
Воспитательные - воспитание познавательной активности, чувства ответственности, уважения друг к другу, взаимопонимания, уверенности в себе; воспитание культуры общения. Воспитывать сознательное отношение к учебе и заинтересованность.
Средства обучения:
- Методическая разработка по теме.
- Электронная презентация по теме.
- Персональный компьютер, медиапроектор.
Внутрипредметные связи: показательная функция и логарифмическая функция.
Межпредметные связи: алгебра и матанализ.
Студент должен знать:
- определение логарифма.
- обозначения и основные свойства логарифмической функции.
Студент должен уметь:
- находить логарифм числа.
- строить график логарифмической функции с данным основанием.
План занятия
1.Организационный момент – 2 мин.
2.Вводная мотивация: постановка целей, изложение плана урока – 3 мин.
3.Проверка домашнего задания – 10 мин.
4.Изучение нового материала - 45 мин.
Основной материал, с использованием электронной презентации по теме: «Логарифмическая функция. Свойства и график»
5.Закрепление материала: Решение задач № 318-322 на стр. – 25 мин.
6.Подведение итогов – 3 мин.
7. Домашнее задание – 2 мин. § 18 Упражнение № 318-322 четные.
Ход урока:
1. Организационный момент .
2. Вводная мотивация: постановка целей, изложение плана урока.
3. Проверка домашнего задания – 10 мин. Письменно на доске проверка § 18 Упражнение № 318-322 четные.
4. Изучение нового материала - 45 мин.
Опр: Функция ![]() ,
, ![]() называется логарифмической функцией.
называется логарифмической функцией.
Логарифмическая функция ![]() является обратной по отношению к показательной функции
является обратной по отношению к показательной функции ![]()
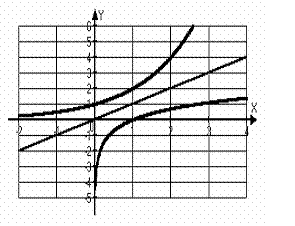
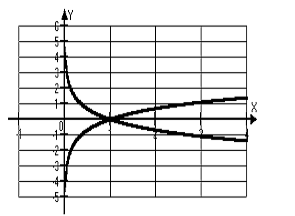
![]() . Поэтому их графики симметричны относительно биссектрисы I и III координатных углов (рис. 8).
. Поэтому их графики симметричны относительно биссектрисы I и III координатных углов (рис. 8).
|
| |
| Рис. 8. |
Приведем основные свойства логарифмической функции:
1) Область определения: ![]() .
.
2) Область значений функции: ![]() .
.
3) Логарифм единицы равен нулю, логарифм основания равен единице: ![]() ,
, ![]() .
.
4) Функция ![]() ,
, ![]() возрастает в промежутке
возрастает в промежутке ![]() (рис. 8 а). При этом, логарифмы чисел, больших единицы, положительны, а - меньших единицы, отрицательны.
(рис. 8 а). При этом, логарифмы чисел, больших единицы, положительны, а - меньших единицы, отрицательны.
5) Функция ![]() ,
, ![]() убывают в промежутке
убывают в промежутке ![]() (рис. 8 б). При этом, логарифмы чисел, меньших единицы, положительны, а - больших
(рис. 8 б). При этом, логарифмы чисел, меньших единицы, положительны, а - больших
5. Закрепление нового материала: Решение упражнений № 318-322 нечетные.
№ 318
1) log 3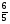 > log 3
> log 3 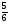 , т.к функция у = log 3 x возрастает.
, т.к функция у = log 3 x возрастает.
3) log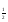 e log
e log 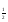 π, т.к функция у = log
π, т.к функция у = log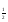 х убывает.
х убывает.
№ 319
-
т.к 3> 1 и 4,5 > 1, то log 3 4,5 > 0.
3)т. К 5 > 1 b 25,3 > 1, то log 5 25, 3 >0.
№ 320
1)log 3 x , т.к 3 > 1, - 0,3 x
3)lg x = 0.2 , т.к 10> 1, 0,2 > 0, то х >1.
№ 321
1)убывает
3)возрастает.
№ 322 у = log 2 х
6. Подведение итогов.
7. Домашнее задание: № 318-322 четные.
План теоретического занятия.
Специальность: 060501 Дисциплина ОДБ. 06 Математика
Тема : «Десятичные и натуральные логарифмы »
Тип занятия: Урок усвоения навыков и умений, комбинированное занятие – с элементами беседы и выполнением упражнений.
Цели занятия:
Образовательные - формирование знаний в усвоении понятия десятичного и натурального логарифмов.
Развивающие - развитие мыслительных операций посредством конкретизации, развитие зрительной памяти, потребности к самообразованию, способствовать развитию познавательных процессов.
Воспитательные - воспитание познавательной активности, чувства ответственности, уважения друг к другу, взаимопонимания, уверенности в себе; воспитание культуры общения. Воспитывать сознательное отношение к учебе и заинтересованность.
Средства обучения:
- Методическая разработка по теме.
- Электронная презентация по теме.
- Персональный компьютер, медиапроектор.
Внутрипредметные связи: десятичный и натуральный логарифм.
Межпредметные связи: алгебра и матанализ.
Студент должен знать:
- определение десятичного и натурального логарифма, формулу перехода от логарифма по одному основанию к логарифму по другому основанию.
- свойства логарифмической функции.
Студент должен уметь:
- находить логарифм числа, применяя формулу перехода от логарифма по одному основания к логарифму другого основания.
- пользоваться таблицей Брадиса и микрокалькулятором при вычислении логарифмов.
План занятия
1.Организационный момент – 2 мин.
2.Вводная мотивация: постановка целей, изложение плана урока – 3 мин.
3.Проверка домашнего задания – 10 мин.
4.Изучение нового материала - 45 мин.
Основной материал, с использованием электронной презентацией по теме: «Десятичные и натуральные логарифмы»
5.Закрепление материала: Решение задач № 301-307 на стр. – 25 мин.
6.Подведение итогов – 3 мин.
7. Домашнее задание – 2 мин. § 17Упражнение № 301-307 четные.
Ход урока:
1. Организационный момент .
2. Вводная мотивация: постановка целей, изложение плана урока.
3. Проверка домашнего задания – 15 мин. Тесты.
Вариант № 1
1. Найдите область определения функции у =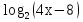
-
( -
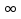 ; +
; +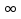 ); 2) (2; +
); 2) (2; +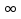 ); 3) ( -
); 3) ( - 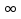 ; 2)
; 2)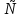 (2; +
(2; +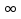 ); 4) [2; +
); 4) [2; +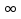 ).
).
2. Найдите значение выражения 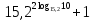
-
21; 2) 101; 3) 11; 4) 15,2.
3. Вычислить:
81log34
а) 16; б) 64; в)256; г)1
4. Сравнить числа:
loge6 loge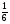
а) log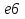 > log e
> log e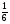 ; в) log
; в) log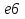 = log e
= log e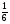 ;
;
б) log 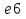 log e
log e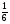 ; г) нельзя определить
; г) нельзя определить
Вариант № 2
1. Найдите область определения функции у =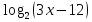
-
( -
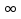 ; +
; +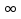 ); 2) (4; +
); 2) (4; +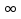 ); 3) ( -
); 3) ( - 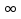 ; 4)
; 4)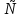 (4; +
(4; +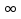 ); 4) [4; +
); 4) [4; +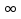 ).
).
2. Найдите значение выражения 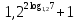
1)50; 2) 7; 3) 1; 4) 1,2.
3. Вычислите: 27log35
а) 5; б) 27; в)125; г)25.
4. Сравните числа: log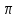 5 log
5 log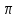
а) log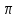 5 > log
5 > log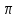 ; в) log
; в) log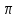 5 = log
5 = log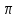 ;
;
б) log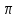 5 log
5 log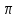 ; г) невозможно определить.
; г) невозможно определить.
4. Изучение нового материала - 45 мин.
Опр: Десятичным логарифмом числа называют логарифм этого числа по основанию 10 ипишут lg b
Опр: Натуральным логарифмом числа называют логарифм этого числа по основанию e, где e - иррациональное число, приближенно равное 2,7. При этом пишут ln b.
Переход к новому основанию логарифма
Логарифмических функций бесконечно много:![]() и т.д. Возникает вопрос, как они связаны между собой? Есть ли, например, какая-то связь между функциями у=log2 х и y=log3 x? На рис. 231 изображены графики функций у=log2 х и у=log3 х. Не кажется ли вам, что график первой функции получается из графика второй функции растяжением от оси х с некоторым коэффициентом к >1. Если наше геометрическое наблюдение верно, то должно выполняться равенство:
и т.д. Возникает вопрос, как они связаны между собой? Есть ли, например, какая-то связь между функциями у=log2 х и y=log3 x? На рис. 231 изображены графики функций у=log2 х и у=log3 х. Не кажется ли вам, что график первой функции получается из графика второй функции растяжением от оси х с некоторым коэффициентом к >1. Если наше геометрическое наблюдение верно, то должно выполняться равенство:
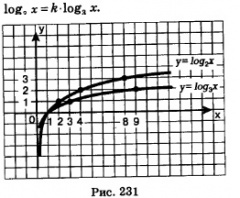
Так ли это? На все поставленные вопросы мы ответим в этом параграфе. Теоретической основой для ответа является следующая теорема.

Теперь нетрудно ответить на поставленный выше вопрос: как связаны между собой различные логарифмические функции? Рассмотрим две логарифмические функции у =log2 х и у =log3 х, графики которых изображены на рис. 231. Имеем:
![]()
Таким образом, наша догадка подтвердилась: действительно, справедливо соотношение
![]() ;
;
подтвердилась и наша догадка о том, что в данном случае к > 1, поскольку log2 3 > 1.
Аналогичные формулы связывают и другие логарифмические функции. Например, справедливы соотношения:
![]()
Рассмотрим два важных частных случая формулы перехода к новому основанию логарифма, два следствия из доказанной теоремы.
Следствие 1. Если а и b положительные и отличные от 1 числа, то справедливо равенство:
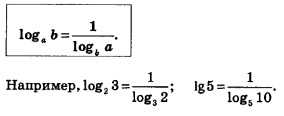
Доказательство. Положив в формуле (1) с =Ь, получим:
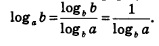
Следствие 2. Если а и b — положительные числа, причем ![]() , то для любого числа
, то для любого числа ![]() справедливо равенство:
справедливо равенство:
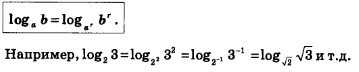
Доказательство. Перейдем в выражении ![]() к логарифмам по основанию а:
к логарифмам по основанию а: 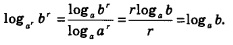
5. Закрепление нового материала:
Пример 1. Дано:
![]()
Решение.
![]()
Пример 2. Решить уравнение:
![]()
Решение. Перейдем во всех логарифмах к одному основанию 4. Для этого дважды воспользуемся формулой, доказанной в следствии 2:
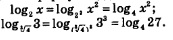
Теперь заданное уравнение можно переписать в более простой форме:
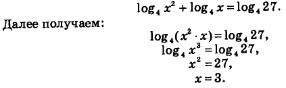
Ответ: х = 3.
6. Подведение итогов.
7. Домашнее задание № 318 – 324.
План теоретического занятия.
Специальность: 060501 Дисциплина ОДБ. 06 Математика
Тема: «Логарифмические уравнения »
Тип занятия: Урок усвоения навыков и умений, комбинированное занятие – с элементами беседы и выполнением упражнений.
Цели занятия:
Образовательные – формирование понятий простейших логарифмических уравнений.
Развивающие - развитие мыслительных операций посредством конкретизации, развитие зрительной памяти, потребности к самообразованию, способствовать развитию познавательных процессов.
Воспитательные - воспитание познавательной активности, чувства ответственности, уважения друг к другу, взаимопонимания, уверенности в себе; воспитание культуры общения. Воспитывать сознательное отношение к учебе и заинтересованность.
Средства обучения:
- Методическая разработка по теме.
- Электронная презентация по теме.
- Персональный компьютер, медиапроектор.
Внутрипредметные связи: десятичный и натуральный логарифм.
Межпредметные связи: алгебра и матанализ.
Студент должен знать:
- знать вид простейших логарифмических уравнений, основные приемы решений логарифмических уравнений.
- свойства логарифмической функции.
Студент должен уметь:
- решать простейшие логарифмические уравнения и применять основные приемы при решении уравнений.
План занятия
1.Организационный момент – 2 мин.
2.Вводная мотивация: постановка целей, изложение плана урока – 3 мин.
3.Проверка домашнего задания – 10 мин.
4.Изучение нового материала - 45 мин.
Основной материал, с использованием электронной презентацией по теме: «Логарифмические уравнения»
5.Закрепление материала: Решение задач № 337-340 на стр. – 25 мин.
6.Подведение итогов – 3 мин.
7. Домашнее задание – 2 мин. § 18 Упражнение № 337- 340 четные.
Ход урока
1.Организационный момент – 2 мин.
2.Вводная мотивация: постановка целей, изложение плана урока – 3 мин.
3.Проверка домашнего задания – 10 мин.
4.Изучение нового материала - 45 мин.
Основной материал, с использованием электронной презентацией по теме: «Логарифм. Свойства логарифмов»
Логарифмические уравнения
Логарифмическими уравнениями называют уравнения вида
![]()
где а — положительное число, отличное от 1, и уравнения, сводящиеся к этому виду.
Опираясь на теорему 4 из § 18, согласно которой равенство
![]()
справедливо тогда и только тогда, когда 1=8, мы можем сформулировать следующее утверждение.
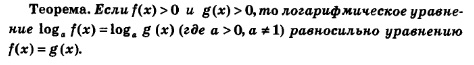
На практике эту теорему применяют так: переходят от уравнения (1) к уравнению f(х) = g(х) (такой переход называют потенцированием), решают уравнение f(х)= g(х), а затем проверяют его корни по условиям f(х) >0, g(х) >0, определяющим область допустимых значений переменной (ОДЗ). Те корни уравнения f(х) = g(х), которые удовлетворяют этим условиям, являются корнями уравнения (1). Те корни уравнения f(х) =g(х), которые не удовлетворяют хотя бы одному из этих условий, объявляются посторонними корнями для уравнения (1).
Пример 1. Решить уравнение:
![]()
Решение.1) Потенцируя (т.е. освободившись от знаков логарифмов ), получаем:
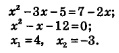
2) Проверим найденные корни по условиям:
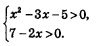
Значение x = 4 не удовлетворяет этой системе неравенств (достаточно заметить, что x = 4 не удовлетворяет второму неравенству системы), т.е. x = 4 — посторонний корень для заданного уравнения. Значение x =-3 удовлетворяет обоим неравенствам системы, а потому х = —3 — корень заданного уравнения.
Ответ: х = -3.
Пример 2. Решить уравнение:
![]()
Решение. 1) Сначала надо преобразовать уравнение к виду (1). Для этого воспользуемся правилом: «сумма логарифмов равна логарифму произведения». Оно позволяет заменить выражение log2(х + 4)+ log2(2x + 3) выражением log2(х + 4)(2x: + 3). Тогда заданное уравнение можно переписать в виде:
![]()
2) Потенцируя, получаем:
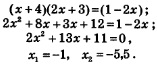
3) Проверим найденные корни по условиям:
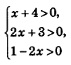
(обратите внимание: условия для проверки всегда определяют по заданному уравнению). Значение x = -1 удовлетворяет этой системе неравенств, а значение х = -5,5 не удовлетворяет (это посторонний корень).
Ответ: х = -1.
Замечание. Иногда удобнее использовать другой порядок ходов: сначала решить систему неравенств — в примере 2 решением системы неравенств будет интервал (-1,5, 0,5); это — область допустимых значений переменной (ОДЗ) или область определения уравнения. Затем найти корни x1 = -1, х2 = -5,5. И, наконец, сделать проверку найденных значений х, но уже не с помощью системы неравенств, а по найденной заранее области допустимых значений. В примере 2 значение x = -1 принадлежит интервалу (-1,5, 0,5), а значение x = -5,5 этому интервалу не принадлежит. Следовательно, х = -5,5 — посторонний корень, т.е. x = -1 — единственный корень заданного логарифмического уравнения.
Пример 3. Решить уравнение:
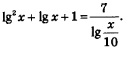
Решение.
Так как
![]()
то заданное уравнение можно переписать в виде
![]()
Есть смысл ввести новую переменную y = lg х; тогда уравнение примет вид
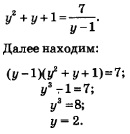
Это значение удовлетворяет условию ![]() (посмотрите: у записанного выше рационального относительно у уравнения переменная содержится в знаменателе, а потому следует проверить, не обращается ли знаменатель в 0 при найденном значении переменной у).
(посмотрите: у записанного выше рационального относительно у уравнения переменная содержится в знаменателе, а потому следует проверить, не обращается ли знаменатель в 0 при найденном значении переменной у).
Итак, у = 2. Но у = lg х, значит, нам осталось решить простейшее логарифмическое уравнение lg х = 2, откуда находим х = 100.
Ответ: х = 100.
Подведем некоторые итоги. Можно выделить три основных метода решения логарифмических уравнений.
1) Функционально-графический метод. Он основан на использовании графических иллюстраций или каких-либо свойств функций. Мы применяли этот метод в § 49.
2)Методпотенцирования. Он основан на теореме, полученной в начале параграфа. Мы применили этот метод в примерах 1 и 2.
3) Метод введения новой переменной. Мы применили этот метод в примере 3.
Завершая параграф, рассмотрим пример, в котором для решения уравнения используется еще один метод — метод логарифмирования, и пример решения системы логарифмических уравнений.
Пример 4. Решить уравнение
![]() Решение. Возьмем от обеих частей уравнения логарифмы по основанию 5; зто — равносильное преобразование уравнения, поскольку обе его части принимают только положительные значения. Получим:
Решение. Возьмем от обеих частей уравнения логарифмы по основанию 5; зто — равносильное преобразование уравнения, поскольку обе его части принимают только положительные значения. Получим:
![]()
позволит переписать заданное уравнение в виде: (l - log5x) ■ log5 х = -2. Замечаем, что «проявилась» новая переменная у = log5 х, относительно которой уравнение принимает весьма простой вид: (1 - у)у = -2. Далее получаем:
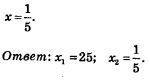
Но у = log5 х, значит, нам осталось решить два уравнения:
log5 x=2, log5 x=-1. Из первого уравнения находим х = 5', т.е. х = 25; из второго уравнения находим x =5 , т.е.
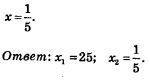
Пример 5. Решить систему уравнений
![]()
Решение. 1) Преобразуем первое уравнение системы к более простому виду:
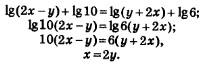
2) Преобразуем второе уравнение системы к более простому виду:
![]()
3) Решим полученную систему уравнений:
![]()
Подставив 2у вместо х во второе уравнение, получим
![]()
Соответственно из соотношения х = 2у находим х2 = 4, х2 = -2. 4) Осталось сделать проверку найденных пар (4; 2) и (-2; -1) с помощью условий, которые мы определяем, анализируя исходную систему уравнений:
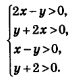
Пара (4; 2) удовлетворяет этим условиям, а пара (-2; -1) не удовлетворяет (например, она «не проходит» уже через первое условие 2х -у> 0).
Ответ: (4; 2).
5.Закрепление материала: Решение задач № 337-340 на стр. – 25 мин.
№ 337
1)log 2 (x -5 ) + log 2 (x + 2) = 3
log 2 (x-5)(x +2) = log2 8
(x-5)(x +2)=8
x-5>0
x+2 > 0
x2 - 3x -18=0
x1 = 6 x2 = -3.
Учитывая область определения логарифмической функции х>5 и x > -2 Ответ: х = 6.
6.Подведение итогов – 3 мин.
7. Домашнее задание – 2 мин. § 18 Упражнение № 337- 340 четные.
План теоретического занятия.
Специальность: 060501 Дисциплина ОДБ. 06 Математика
Тема : «Логарифмические неравенства»
Тип занятия: Урок усвоения навыков и умений, комбинированное занятие – с элементами беседы и выполнением упражнений.
Цели занятия:
Образовательные – формирование понятий простейших логарифмических неравенств.
Развивающие - развитие мыслительных операций посредством конкретизации, развитие зрительной памяти, потребности к самообразованию, способствовать развитию познавательных процессов.
Воспитательные - воспитание познавательной активности, чувства ответственности, уважения друг к другу, взаимопонимания, уверенности в себе; воспитание культуры общения. Воспитывать сознательное отношение к учебе и заинтересованность.
Средства обучения:
- Методическая разработка по теме.
- Электронная презентация по теме.
- Персональный компьютер, медиапроектор.
Внутрипредметные связи: логарифмические неравенства и уравнения.
Межпредметные связи: алгебра и матанализ.
Студент должен знать:
- знать вид простейших логарифмических неравенств, основные приемы решений логарифмических неравенств.
- свойства логарифмической функции.
Студент должен уметь:
- решать простейшие логарифмические неравенства и применять основные приемы при решении неравенств.
План занятия
1.Организационный момент – 2 мин.
2.Вводная мотивация: постановка целей, изложение плана урока – 3 мин.
3.Проверка домашнего задания – 10 мин.
4.Изучение нового материала - 45 мин.
Основной материал, с использованием электронной презентацией по теме: «Логарифмические неравенства»
5.Закрепление материала: Решение задач № 354-357 на стр. – 25 мин.
6.Подведение итогов – 3 мин.
7. Домашнее задание – 2 мин. § 20 Упражнение № 354- 357 четные.
Ход урока
1.Организационный момент.
2.Вводная мотивация: постановка целей, изложение плана урока.
3.Проверка домашнего задания – Письменно на доске № 337-340
4.Изучение нового материала.
Основной материал, с использованием электронной презентацией по теме: «Логарифмические неравенства».
Теоретическая часть:
Алгоритм решения логарифмического неравенства.
1.Найти область определения неравенства (подлогарифмическое выражения больше нуля).
2.Определить, возрастающей или убывающей является логарифмическая функция. ( если основание а> 1, то функция возрастает. Если 0a
3.Переходим к более простому неравенству (подлогарифмических выражений); знак неравенства сохраняется, если функция возрастает, знак меняется, если функция убывает.
4.Решаем полученное неравенство, учитывая область определения исходного неравенства.
Пример:
log3(x – 5) log x2
1)Область определения неравенства х – 5> 0 и х 2 > 0. Значит,
x> 5.
2)Функция у = log3х возрастает, т.к 3>1.
3)x2 –x +5>0. Неравенство верно при любом действительном х.
4)Решение неравенства: х>5.
Практическая часть: № 354 – 357 (нечетные).
Закрепление нового материала:
Вариант 1
-
Укажите множество решений неравенства:
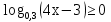
а)( – 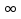 ; 3] б) [3; +
; 3] б) [3; + 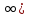 в) (
в) (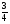 ; 1]; г) (3,5; +
; 1]; г) (3,5; + 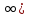
2. Найдите значение выражения: log3 log77 – log5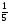
а) 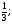 б) -1; в) 1; г) 7
б) -1; в) 1; г) 7
3. Укажите промежуток, которому принадлежит корень уравнения 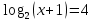
1) (8; 10); 2) (14; 16); 3) (6; 8); 4) (4; 6).
Вариант 2
1.Укажите множество решений неравенства:
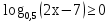
а) ( – 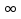 ; 4] б) [4; +
; 4] б) [4; + 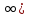 в) (3,5; 4]; г) (3,5; +
в) (3,5; 4]; г) (3,5; + 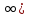 .
.
2.Найдите значение выражения: log7 log1111 – log9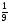
а) 1; б) -1; в) 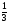 ; г)
; г) 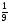
3. Укажите промежуток, которому принадлежит корень уравнения lg 5x = 2
-
(8;10); 2) (14;16); 3) (19;21); 4) (94;96).
6.Подведение итогов – 3 мин.
7. Домашнее задание – 2 мин. § 18 Упражнение № 354- 357 четные.
Здесь представлен конспект к уроку на тему «Логарифмы. Свойства логарифмов», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.