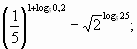Конспект урока «Свойства логарифмов» по алгебре для 11 класса
Урок по алгебре и началам анализа в 11 классе
Тема: Свойства логарифмов.
Цель:
-
Организовать работу учащихся по изучению и применению свойств логарифмов.
-
Способствовать овладению учащимися основными алгоритмическими приемами применения изученных свойств при вычислении логарифмов, развитию внимания, мышления и памяти в процессе воспроизведения и применения формул.
-
Содействовать формированию коммуникативных навыков при работе в парах, привитию ответственного отношения к учебе.
Учебное обеспечение: Колмогоров А.Н. Алгебра и начала анализа. Учебник для 10-11 классов общеобразовательных учреждений. - М.: Просвещение, 2007.
Оборудование: мультимедийный компьютер, рабочие карты урока, карточки с заданиями.
| Этап урока | Время | |
| I | Организационный момент | 2 мин |
| II | Повторение. Решение заданий части А (ЕГЭ) | 5 мин |
| III | Актуализация знаний. Постановка проблемы. Сообщение «Логарифмы в природе» | 4 мин |
| IV | Постановка целей и задач урока | 2 мин |
| V | Изучение нового материала | 8 мин |
| VI | Работа в парах | 20 мин |
| VII | Домашнее задание | 1 мин |
| VIII | Итог урока | 3 мин |
ХОД УРОКА
-
Организационный момент. Объяснение учителя порядка работы. Знакомство с рабочей картой урока.
РАБОЧАЯ КАРТА УРОКА
ФИ учащегося __________________________________
| Этапы урока | Задание | Отметка о выполнении | ||
| 1 | Организационный момент | Соберись. Настройся на урок. | | |
| | ||||
| 2 | Повторение. Тест (ЕГЭ часть А) | «3» | 3 – 4 верных ответа | |
| «4» | 5 верных ответов | | ||
| «5» | 6 верных ответов | | ||
| | ||||
| 3 | Ознакомление с новым материалом | Смотри. Слушай. Вспоминай. Записывай. | | |
| | ||||
| 4 | Выполнение заданий на применение формулы логарифма произведения | «3» | | |
| «4» | | | ||
| «5» | | | ||
| | ||||
| 5 | Выполнение заданий на применение формулы логарифма частного | «3» | | |
| «4» | | | ||
| «5» | | | ||
| | ||||
| 6 | Выполнение заданий на применение формулы логарифма степени | «3» | | |
| «4» | | | ||
| «5» | | | ||
| | ||||
| 7 | Формула перехода логарифма к другому основанию | «3» | | |
| «4» | | | ||
| «5» | | | ||
| Доп. | Задание на применение всех формул | | | |
| | ||||
| 8 | Самооценка за урок | | | «3» |
| | | «4» | ||
| | | «5» | ||
| | ||||
| 9 | Домашнее задание: п.37 весь, свойства знать | «3» | № 494 аб, 495 аб, 496 ав | |
| «4» | № 494 вг, 495 вг, 496 бг, 497 вг | | ||
| «5» | Глава V. Задачи на повторение, п.7, № 66 | | ||
| | ||||
| 10 | Итог урока. Рефлексия. | | | |
-
Повторение. Решение заданий части А ЕГЭ. Выполнить задания с выбором ответа, сделать самопроверку (Приложение 1). Отметить количество допущенных ошибок.
-
Актуализация знаний. Проблема: Как найти значение такого выражения? (Приложение 2).
-
Постановка целей и задач урока. Повторить свойства степени, определение логарифма, процитировать слова Дж. Непера.
На прошлом уроке вы ознакомились с понятием логарифма, рассмотрели основные примеры нахождения логарифмов. Но чтобы успешно использовать на практике операцию логарифмирования, необходимо познакомиться со свойствами этой операции. Итак, тема урока «Свойства логарифмов». Формулируем цели урока.
-
Изучение нового материала. Обсуждение свойств идет с использованием презентаций при активном участии детей. Свойства записываются в тетради. Продумывается название свойства. Уточняется область определения входящих в формулы буквенных величин. Добавляются полезные, изученные ранее, свойства (частные случаи).
-
Самостоятельная работа учащихся. Работа некоторых учащихся у доски.
VIII . Итог урока. Рефлексия.
Выполнил ли задания намеченного уровня сложности?
Если не выполнил – почему?
Кто перешел на более высокий?
Что нужно сделать дома?
| Карточка 2 | |
| log a 1 = | log a a = |
| log a | log a |
| log a | log aа m = |
| log a (xy) = | log a |
| log a xp = | log a b = |
5. Самостоятельная работа проверочного характера
Ребята, вам даются задания, которые вы должны выполнить. Получив ответы к каждому заданию, внизу таблицы выберите свои ответы и рядом с заданием, в пустые клеточки впишите соответствующие значения букв.
Вариант 1
| Вычислите |
| |||||||||
| 2. | Вычислите |
| ||||||||
| 3. | Вычислите |
| ||||||||
| 4. | Вычислите |
| ||||||||
| 5. | При каких значениях х имеет смысл выражение |
| ||||||||
| | Е | Ю | Б | И | Р | Г | Н | П | ||
| |
| -1 |
|
| 1 | -6,5 |
| 2 | ||
Вариант 2
| Вычислите |
| |||||||
| 2. | Определите знак разности |
| ||||||
| 3. | Вычислите |
| ||||||
| 4. | При каких значениях х имеет смысл выражение |
| ||||||
| 5. | Вычислите |
| ||||||
| Ю | Е | Б | И | Р | Г | Н | П | |
| -1 |
|
|
| 1 | -6,5 |
| 2 | |
Проверка ответов самостоятельной работы.
У 1-го варианта получилось Бюрги, у 2-го варианта – Непер. Это фамилии двух известных математиков: шотландца Джона Непера (1550 – 1617) и швейцарца Иобстома Бюрги (1552 – 1632), которыми одновременно и независимо друг от друга были изобретены логарифмы.
Немного из истории логарифмов
Логарифмы были придуманы для ускорения и упрощения вычислений.
Бурное развитие науки, техники и мореплавания в эпоху Возрождения, быстрое развитие астрономии и усложнение арифметических выкладок настоятельно требовали новых способов вычислений, которые позволили бы ускорить вычисления, сделать их доступными более широкому кругу людей.
К концу XVI в. астрономы, например, пользовались 10-тизначными таблицами тригонометрических функций. Значит, им приходилось производить многочисленные выкладки с 10-значными числами. Выкладки эти отнимали очень много времени и не всякому были под силу.
Нужен был способ ускорить вычисления.
Этим способом или, как говорят, вспомогательным вычислительным аппаратом, явились логарифмы.
Почва для развития логарифмов была подготовлена всем предшествующим развитием математики.
У древнегреческого ученого Диофанта в зачаточной форме есть действия над степенями одного и того же основания; французской ученый Оресм (XIV в.) вводит дробные показатели; другой французский ученый Шюке (XV в.) ввел нулевой и отрицательный показатель; фламандский ученый XVI в. Стевин составил таблицы процентных расчетов.
Таким образом, к концу XVI в. были подготовлены условия создания логарифмов.
Идея логарифма, т.е. идея выражать числа в виде степени одного и того же основания, принадлежит Михаилу Штифелю. (Предвосхищение этой идеи можно видеть у Архимеда.) Но во времена Штифеля математика была не столь развита и идея логарифма не нашла своего развития.
Логарифмы были изобретены позже одновременно и независимо друг от друга шотландским ученым Джоном Непером (1550-1617) и швейцарцем Иобстом Бюрги (1552-1632).
Первым опубликовал работу Непер в 1614 г. под названием “Описание удивительной таблицы логарифмов”. Теория логарифмов Непером была дана в достаточно полном объеме, способ вычисления логарифмов дан наиболее простой, поэтому заслуги непера в изобретении логарифмов больше, чем у Бюрги.
Бюрги работал над таблицами одновременно с Непером, но долгое время держал их в секрете и опубликовал лишь в 1620 г.
Здесь представлен конспект к уроку на тему «Свойства логарифмов», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (11 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.