Конспект урока «Функция» по алгебре для 8 класса
ПЛАН-КОНСПЕКТ УРОКА
Функция![]()
| ФИО | Кнаус Татьяна Владимировна | |
| | Место работы | МБОУ «Гимназия 38» |
| | Должность | Учитель математики |
| | Предмет | Алгебра |
| | Класс | 8 |
| | Тема и номер урока в теме | «Квадратичная функция» (16 уроков, урок 4) |
| | Базовый учебник | Ш.А. Алимов, Ю.М. Колягин, Ю.В.Сидоров и др. «Алгебра 8», М: Просвещение, 2010г, |
-
Цель и задачи урока
Цель: рассмотреть функцию ![]() , изучить ее свойства, построить график
, изучить ее свойства, построить график
Задачи:
- обучающие:
-
повторить алгоритмы построения графика функции
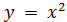 ;
; -
исследовать зависимость графика функции
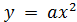 от коэффициентов а;
от коэффициентов а;
-
изучить свойства функции
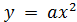
-
Формирование у учащихся навыков исследовательской деятельности, умения анализировать, рассуждать и на основании этого делать выводы
-развивающие:
-
развитие познавательного интереса к обучению математики через использование ИКТ,
-
развитие логического мышления,
-воспитательные
-
Прививать интерес к предмету на основе связи с жизнью
-
Добиться сознательного усвоения материала
-
Тип урока: урок введения нового материала
-
Формы работы учащихся: фронтальная, индивидуальная и групповая работа.
-
Необходимое техническое оборудование: компьютеры (компьютерный класс), интернет, проектор.
-
Структура и ход урока
СТРУКТУРА И ХОД УРОКА
| Этап урока | Название используемых ЭОР | Деятельность учителя (с указанием действий с ЭОР, например, демонстрация) | Деятельность ученика | Время (в мин.) |
||
| 10 мин | |||||
| 1.1 | Актуализация | №1 – Информационный (Функция y=x2 и ее график. И1) | На прошлых уроках мы изучили функцию - Как называется такая функция? - Какими свойствами она обладает? (Индивидуальное задание у доски: Определить, какие точки принадлежат графику функции : А(2;5),В(-2;4),С( | Смотрят ролик. Обсуждают - квадратичная - перечисляют свойства Ученик индивидуально работает у доски. | 5 | |
| 1.2 | Мотивация. | | В физике существует такая формула пути, пройденного телом при равноускоренном движении: S = где a – ускорение (м2/сек), t – время (сек) S – путь (м). Запишите функцию зависимости пройденного пути от времени, если ускорение составило: 1 ряд- 4 м2/сек 2 ряд - 1 м2/сек 3 ряд - 6 м2/сек Что общего и чем отличаются данные функции от функции | 1 ряд - S = 2 ряд - S = 3 ряд - S =
| 3 | |
| 1.3 | Постановка учебной задачи. | | Как вы считаете, чем мы сегодня займемся на уроке? | формулируют цели урока,. -Будем изучать функцию | 1 | |
| 1.4 | Планирование решения учебной задачи. | | - Сегодня на уроке мы рассмотрим функцию | Пишут тему урока в тетрадь. | 1 | |
| 31 мин | |||||
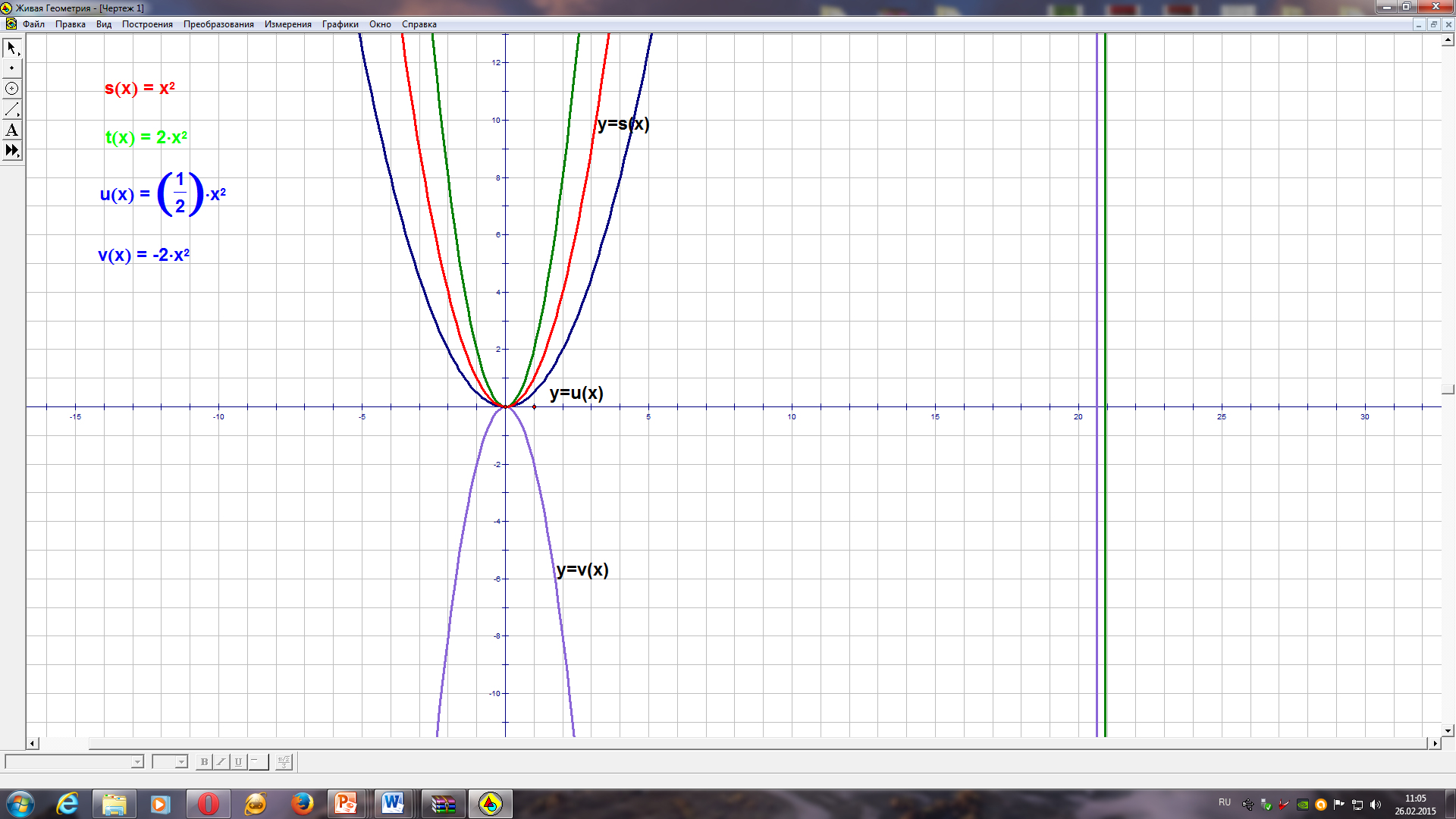
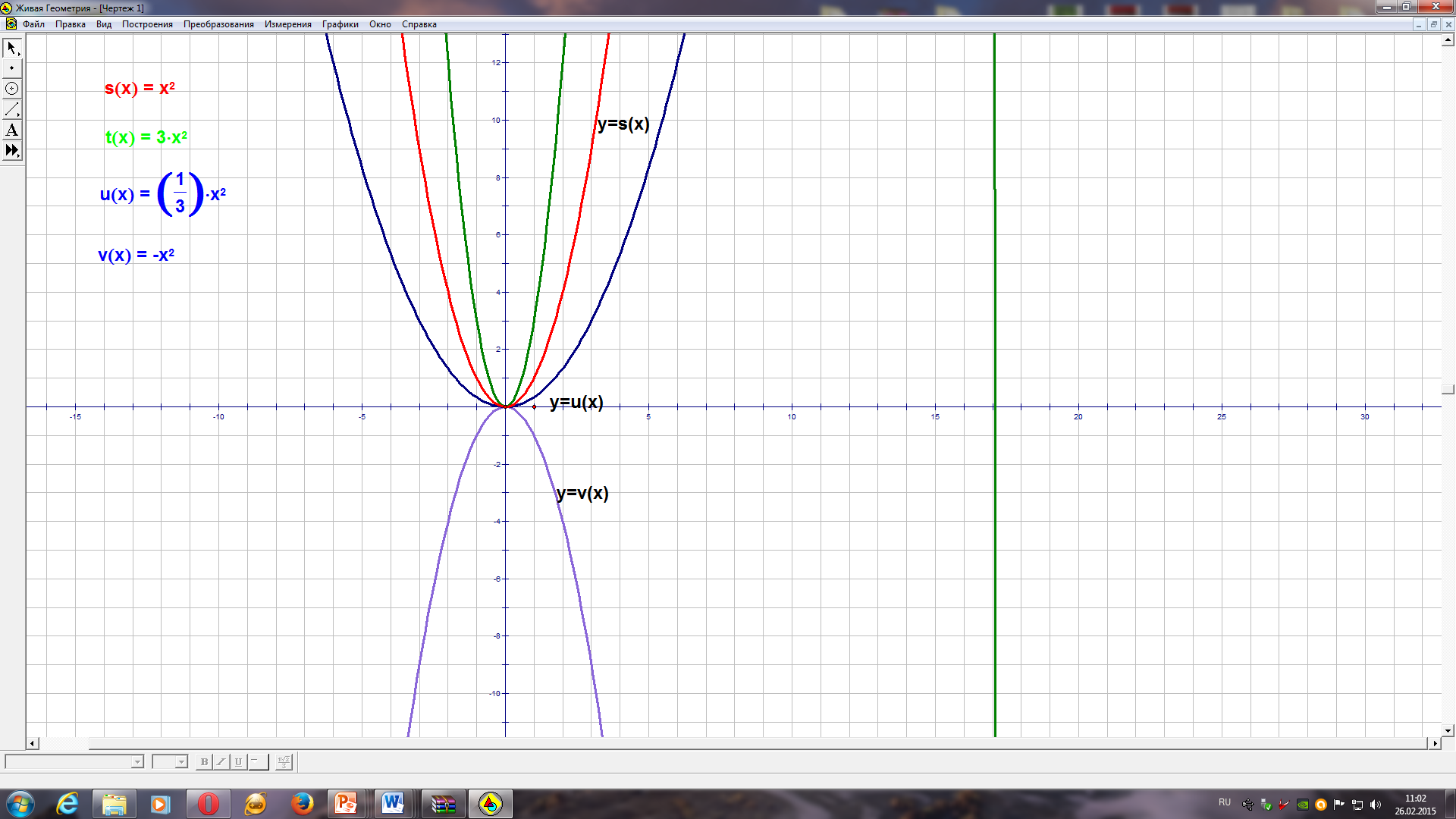
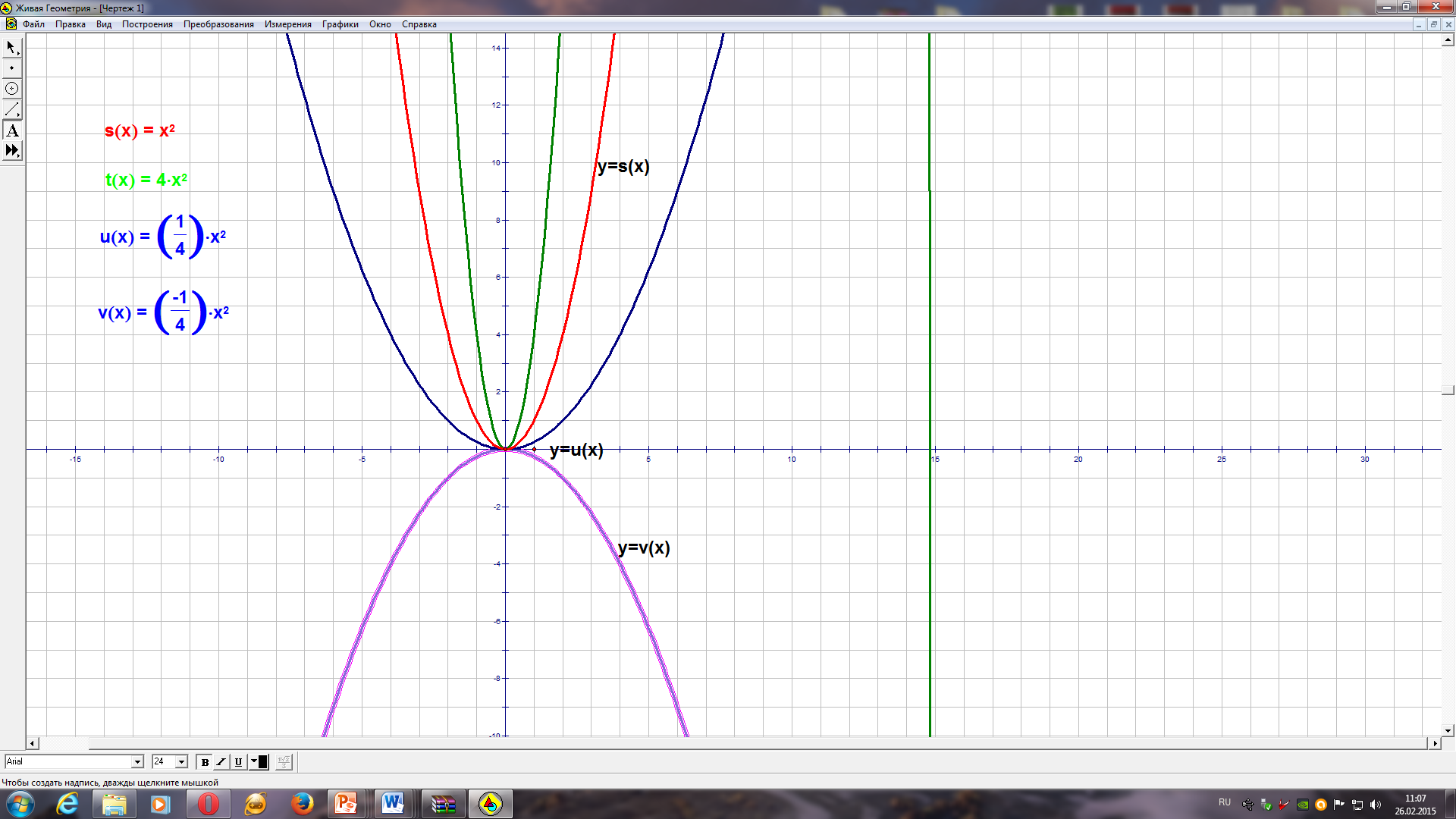
| 2.1. | Открытие новых знаний и способов действий | | Учащимся предлагается выполнить практическую работу (в компьютерной среде «Живая геометрия»). Получают инструкции (приложение 1) | Выполняют работу по 2-3 человека за компьютером. Результат: 1 вариант 2 вариант | 12 мин | |
| | | | Учитель предлагает учащимся выяснить зависимость графика квадратичной функции в зависимости от коэффициентов. Говорят, что график функции У = получается: - растяжением графика У = - сжатием графика У = - симметричен графику У = | 3 вариант 1 вариант Все точки графика функции У = 2 Все точки графика функции y = можно получить из графика функции У = Все точки графика функции У = - 2, 3 вариант (аналогичные объяснения)
| | |
| | Введение нового материала. Формулировка свойств функции У = | | Ученикам предлагается заполнить опорный конспект «свойства функции У = Учитель координирует деятельность учащихся | Работают в группах по 3-4 человека, составляют опорный конспект. Затем происходит обсуждение | 4 мин | |
| | Физкультминутка | | | | | |
| 2.2 | Воспроизведение изученного и его применение в стандартных ситуациях | №2 - тест(Квадратичная функция, ее график и свойства. П1) | Учитель организует фронтальную работу класса. При выполнении заданий модуля необходимо заострить внимание на теоретических аспектах решений задач. Учитель задает вопросы, связанные с ходом решения задач, при необходимости корректируя ответы учащихся. | Ученики выполняют задание, обосновывают решение, приходят к единому мнению. | 15 мин | |
| 2.3. | Перенос новых знаний в новые условия. | №3 - тест (Составление формулы для функции по ее графику. П3) | Параллельно сильным учащимся может быть предложен ЭОР в форме лабораторной работы из 2 заданий на нахождение значений параметров. | Сильные учащиеся выполняют индивидуально задания теста. | | |
| 4 мин | |||||
| 3.1 | Итоги урока. | | - Настала пора подвести итоги работы. Какую цель мы ставили к уроку? Достигнута ли она? Учитель выставляет оценки. | (Ученики отвечают) | | |
| 3.2 | Планирование дальнейшей учебной деятельности. | | Сегодня вы строили график с помощью компьютера, но вы должны уметь строить его и в тетради, на следующем уроке мы поработаем с подобными заданиями. | | | |
| 3.3 | Задание на дом. | | П.37, № 595, 604* | Записывают домашнее задание, задают вопросы | | |
Приложение к плану-конспекту урока
«Признаки параллельности прямых»
Таблица 2.
ПЕРЕЧЕНЬ ИСПОЛЬЗУЕМЫХ НА ДАННОМ УРОКЕ ЭОР
| Название ресурса | Тип, вид ресурса | Форма предъявления информации (иллюстрация, презентация, видеофрагменты, тест, модель и т.д.) | Гиперссылка на ресурс, обеспечивающий доступ к ЭОР | |
| 1 | Функции y=x2 и ее график. И1 | информационный | Интерактивная лекция | http://fcior.edu.ru/card/10276/funkcii-y-x2-i-ee-grafik-i1.html |
| 2 | Квадратичная функция, ее график и свойства. П1 | практический | тест | http://fcior.edu.ru/card/1355/kvadratichnaya-funkciya-ee-grafik-i-svoystva-p1.html |
| 3 | Составление формулы для функции по ее графику. П3 | практический | тест | http://fcior.edu.ru/card/3587/sostavlenie-formuly-dlya-funkcii-po-ee-grafiku-p3.html |
Приложение1.
Инструкция для выполнения практической работы
1 группа
-
Откройте приложение «Живая геометрия»
-
Постройте график функции У =
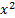
Для этого на горизонтальной панели выбрать «Графики», далее «Построить график функции», набираем x^2 «готово», в меню «свойства» меняем толщину линии и выбираем красный цвет, добавить подпись графика
-
Строим график функции У = 2
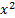 в этом же окне, цвет линии – зеленый (см.п.2)
в этом же окне, цвет линии – зеленый (см.п.2) -
Строим график функции y =
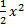 в этом же окне, цвет линии – синий (см.п.2)
в этом же окне, цвет линии – синий (см.п.2) -
Строим график функции У = -
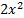 в этом же окне, цвет линии – фиолетовый (см.п.2)
в этом же окне, цвет линии – фиолетовый (см.п.2)
Инструкция для выполнения практической работы
2 группа
-
Откройте приложение «Живая геометрия»
-
Постройте график функции У =
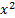
Для этого на горизонтальной панели выбрать «Графики», далее «Построить график функции», набираем x^2 «готово», в меню «свойства» меняем толщину линии и выбираем красный цвет, добавить подпись графика
-
Строим график функции У =
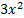 в этом же окне, цвет линии – зеленый (см.п.2)
в этом же окне, цвет линии – зеленый (см.п.2) -
Строим график функции y =
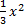 в этом же окне, цвет линии – синий (см.п.2)
в этом же окне, цвет линии – синий (см.п.2) -
Строим график функции y = -
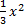 в этом же окне, цвет линии – фиолетовый (см.п.2)
в этом же окне, цвет линии – фиолетовый (см.п.2)
Инструкция для выполнения практической работы
3 группа
-
Откройте приложение «Живая геометрия»
-
Постройте график функции У =
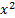
Для этого на горизонтальной панели выбрать «Графики», далее «Построить график функции», набираем x^2 «готово», в меню «свойства» меняем толщину линии и выбираем красный цвет, добавить подпись графика
-
Строим график функции У =
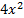 в этом же окне, цвет линии – зеленый (см.п.2)
в этом же окне, цвет линии – зеленый (см.п.2) -
Строим график функции y =
 в этом же окне, цвет линии – синий (см.п.2)
в этом же окне, цвет линии – синий (см.п.2) -
Строим график функции У =
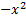 в этом же окне, цвет линии – фиолетовый (см.п.2)
в этом же окне, цвет линии – фиолетовый (см.п.2)
Приложение 2.
Опорный конспект «свойства функции У = ![]() ».
».
Графиком функции У = ![]() , а
, а ![]() 0 является ……
0 является ……
| а > 0 | а | |
| График | Ветви параболы направлены | Ветви параболы направлены |
| Область определения | | |
| Область значений | | |
| Нули функции | Х = | Х = |
| Функция возрастает | | |
| Функция убывает | | |
Здесь представлен конспект к уроку на тему «Функция», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (8 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.