Конспект урока «Квадратичная функция и ее свойства» по алгебре
Фильченко И.А., учитель математики МОУ «Новопетровская ООШ» Кулундинский район Алтайский край
Квадратичная функция и ее свойства
Цели урока:
-
систематизировать знания учащихся по теме «Квадратичная функция», актуализировать и проверить знания и навыки самостоятельной работы по данному разделу;
-
развитие навыка применения актуализированных теоретических знаний при решении практических упражнений;
-
развитие логики и строгости мышления, правильности и культуры устной речи;
-
формирование положительной мотивации к предмету через нестандартную форму реализации урока, развитие познавательного интереса учащихся.
Оборудование и материалы: - компьютер, карточки с текстами работ.
Программное обеспечение: Microsoft Power Point, Microsoft Word.
Структура урока:
I. Организационный этап.
II. Актуализация знаний.
III. Этап оперирования знаниями.
Работа по карточкам.
Индивидуальная работа по графику.
V. Подведение итогов.
Ход урока.
I. Организационный этап.
Учащимся сообщается тема урока, цели урока, формы работы на уроке.
II. Актуализация знаний.
Повторение теоретического материала (фронтальная работа с классом).
Все вопросы и задания высвечиваются на слайдах. (слайд2)
Какую функцию называют квадратичной?
Из приведенных примеров укажите те функции, которые являются квадратичными.
Примеры:
у=5х+1;
у=3х2-1;
у=-2х2+х+3;
у=x3+7x-1;
у=4х2;
у=-3х2+2х.
Что является графиком квадратичной функции?
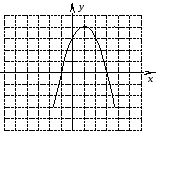
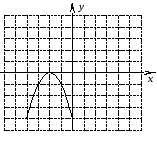
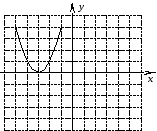
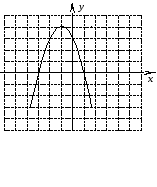
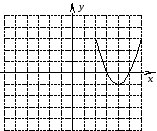
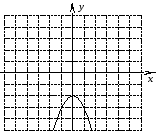
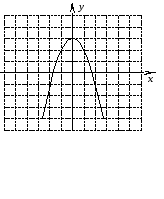
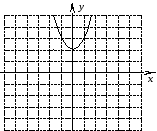
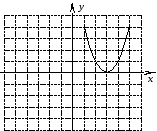
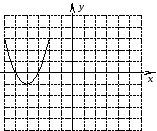
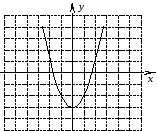
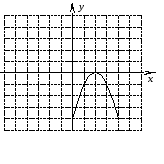
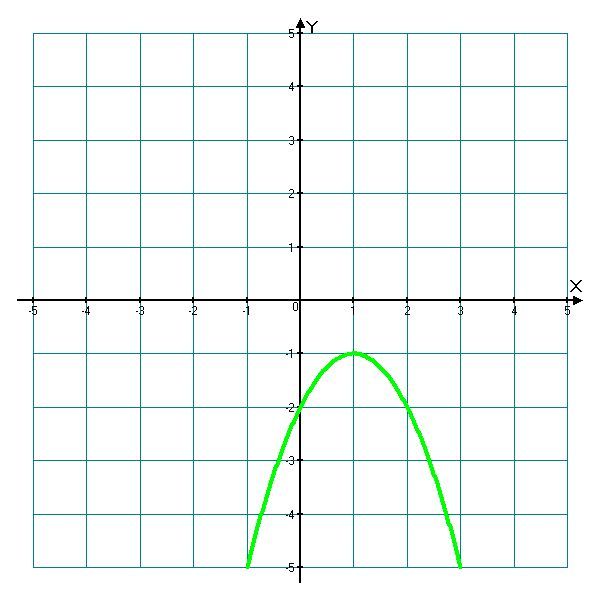
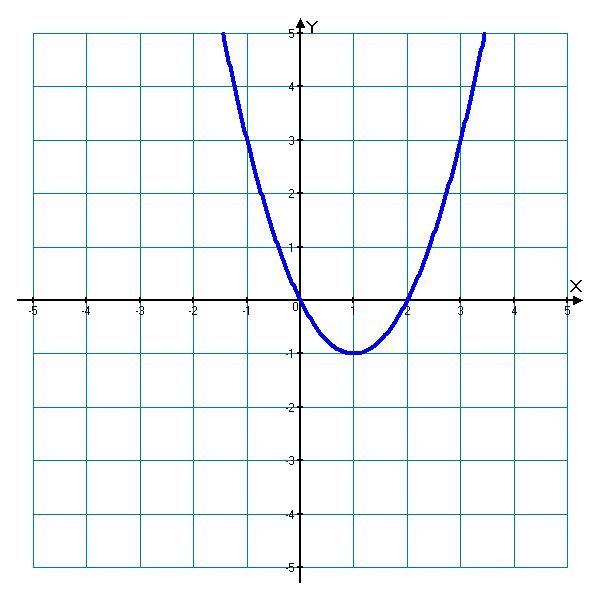
От чего зависит направление ветвей параболы? Определите знак коэффициента a у парабол, изображенных на рисунке (слайд3)
III. Этап оперирования знаниями
По рисунку определите знаки коэффициента а и дискриминанта D.
(Настроенная анимация по щелчку мыши высвечивает правильные ответы)(Слайд4)
|
|
|
|
|
| |
| D>0;a>0 |
|
|
|
|
|
| D>0;a |
|
|
|
|
|
| D0 |
|
|
|
|
|
| D |
|
|
|
|
|
| D=0;a>0 |
|
|
|
|
|
| D=0;a |
|
|
|
|
|
Как найти координаты вершины параболы?
Задание.
Найти координаты вершины параболы: (Слайд5)
у = х2 -4х-5;
у=-5х2+3.
Какой вид имеет уравнение оси симметрии параболы?
Как найти координаты точек пересечения параболы с осями координат (слайд 6)
Координаты точек пересечения параболы с осями координат.
С Ох: у=0
х2+bх+с=0
С Оу: х=0
у=с
Задание.
Найти координаты точек пересечения параболы с осями координат:
1)у=х2-х; 2)у=х2+3; 3)у=5х2-3х-2
Ответы: (0;0);(1;0) (0;3) (1;0);(-0,4;0);(0;2)
Учащимся предлагается выполнить тест (слайд 7).
Для каждой из функций, графики которых изображены, выберите соответствующее условие и отметьте знаком «+».
| у0 | у0 | у>0 | у>0 | у0 | |
|
|
|
|
|
|
|
| (-1;1) |
|
|
|
|
|
| (-∞;0)U U (1;∞) |
|
|
|
|
|
| (-∞;∞) |
|
|
|
|
|
| (-1;0) |
|
|
|
|
|
| х≠-1 |
|
|
|
|
|
| Нет значений х |
|
|
|
|
|
После того, как учащиеся закончили решение тестов, выполняем самопроверку: учащиеся по очереди комментируют свои ответы, на экране с помощью анимации появляются правильные ответы. После проверки учащиеся оценивают свою работу по следующему критерию:
«5» - нет ошибок;
«4» - 1 ошибка;
«3» - 2 ошибки;
«2» - 3 и более ошибки.
Задание.
Построить график функции у= -х2-6х-8 и по графику выяснить ее свойства.
(Учащиеся выполняют задания в тетрадях; один человек работает у доски. Свойства функции с помощью анимации высвечиваются на экране) (слайд 8)
Если учащиеся успевают выполнить все задания и осталось время, то в зависимости от количества компьютеров ( у нас в школе в кабинете их всего 2) даю задание «Квадратичная функция, квадратные уравнения» с сайта www.mathvaz.ru в виде тренировочных упражнений. Остальные работают с
тестами.
| 1. у = –х2 – 2 4. у = (х + 3)27. у = –(х + 2)2 2. у = (х – 3)25. у = –(х – 1)2 + 4 8. у = 4 – (х – 1)2 3. у = (х + 4)2 – 1 6. у = –х2 + 3 9. у = х2 + 2 | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Слово: |
| | | | | | | | | | |
| |
| |
| | |
| | | | | | |
|
| |
| |
| |
| | | | | | |
|
| |
| |
| |
| | | | | | |
|
| |
| |
| |
| | | | | | |
V. Подведение итогов
В конце урока учитель подводит итоги урока и выставляет отметки наиболее активным ученикам.
Здесь представлен конспект к уроку на тему «Квадратичная функция и ее свойства», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.