Конспект урока «Квадратичная функция» по алгебре для 9 класса

Интегрированный урок алгебра-информатика в 9 классе «Квадратичная функция»

(с применением математического пакета MathCAD)

Урок разработала учитель математики и информатики МКОУ «ЛСОШ №68»

Катковская Галина Викторовна

Презентация к уроку

Цели:

• закрепить умение строить графики квадратичной функции и по графику определять ее основные свойства,

• используя свойства квадратичной функции решать задачи

• повышать уровень учебной мотивации с использованием компьютерных технологий, развивать логическое мышление.

К уроку подготовлена презентация. На экране учащиеся видят геометрические фигуры, в которых записаны уравнения. Натуральные числа, являющиеся решениями данных уравнений показывают очередность выполнения заданий на уроке.

Ход урока:

- Сегодня мы попробуем объединить знания, полученные на уроках алгебры, привлекая компьютер к решению математических задач. У каждого из вас на столе лежат карточки с разными выражениями лиц. Определите фигуру, которая соответствует вашему эмоциональному состоянию на начало урока и поставьте около этой фигуры цифру 1. В конце урока вы сделаете то же самое. Это поможет мне определить ваше отношение к такой форме проведения урока.

Отметили? Итак, начнем! Пожалуйста, занимайте свои рабочие места за компьютером. В основе нашего урока лежит презентация. Решив предложенный ребус, вы узнаете тему нашего урока.

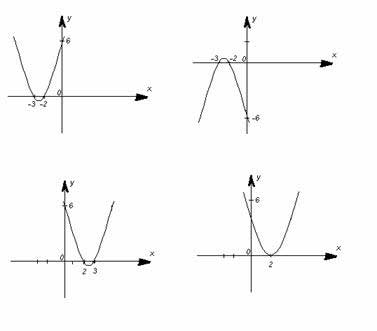
- Итак, тема нашего урока «Квадратичная функция». Мы обобщим знания, полученные при изучении квадратичной функции. Переходим к следующему слайду. На слайде вы видите геометрические фигуры, из которых состоит наш урок. За каждой геометрической фигурой спрятан этап урока. На каждой фигуре записаны уравнения. Какие это уравнения? Как вы видите фигур 5, следовательно, этапов урока тоже 5. Натуральные числа, являющиеся решениями уравнений, будут показывать очередность выполнения заданий на уроке.

I. Заполни пропуски… /повторение свойств квадратичной функции/.

-Первый этап урока обозначается естественно цифрой 1, но где, на какой фигуре спряталось это натуральное число? Для этого найдите корни уравнений, если корнем уравнения является натуральное число 1, то это и есть 1 этап урока. /Ребята прикидывают в уме решение каждого уравнения и определяют, что это – круг./

Итак, переходим к первому этапу нашего урока. Вы должны заполнить пропуски, чтобы получилось верное утверждение или правильная формулировка определения, правила, все ответы-пропуски выпишите в тетрадь, соблюдая нумерацию на слайде.

1. Функция у = aх² + bx + c, где а, b, c – заданные действительные числа, а ≠ 0, х - действительная переменная, называется … функцией.

2. График функции у = ах² при любом а ≠ 0 называют ...

3. Функция у = х² является … (возрастающей, убывающей) на промежутке х ≤ 0.

4. Значения х, при которых квадратичная функция равна нулю, называют … функции.

5. Точку пересечения параболы с осью симметрии называют … параболы.

6. При а >0 ветви параболы у = ах² направлены … .

7. Если а 2 принимает …/положительные, отрицательные/ значения.

II. Подумай… /устные задания/.

-Переходим ко второму этапу урока. Но решением, какого уравнения является натуральное число 2? /учащиеся говорят, что число 2 входит во множество решений уравнения, записанного на параллелограмме/.

За параллелограммом прячутся следующие задания:

1. Найдите координаты вершины параболы у=х²-4х+4

2. Найдите нули квадратичной функции у=х²+х-2

3. Не производя построение графика, определите, наибольшее или наименьшее значение принимает квадратичная функция у=2-5х-3х²

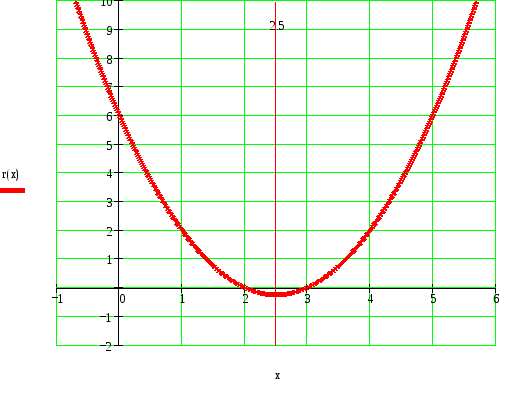
4. По графику найдите значения х, при которых значения функции у = х² - 5х + 6 положительны, отрицательны, равны нулю. Найдите промежутки возрастания и убывания функции.

III. Реши… /работа в группах/.

-За какой геометрической фигурой скрывается следующий этап нашего урока? /ребята определяют, что это трапеция/.

На этом этапе урока ребята работают в группах. Каждой группе предлагается решить определенное задание. После того как все ребята в группе решили это задание, 1 ученик выходит и оформляет решение на доске. Если остается время, то ребята продолжают решать задания, предназначенные для других групп.

• 1 группа: Найти значения х, при которых квадратичная функция у=2х² -5х+3 принимает значение, равное 1.

• 2 группа: Найдите координаты точек пересечения параболы у = х² + х - 12 с осями координат.

• 3 группа: Не строя график функции у = х² – 4х + 6, найти ее наибольшее или наименьшее значение.

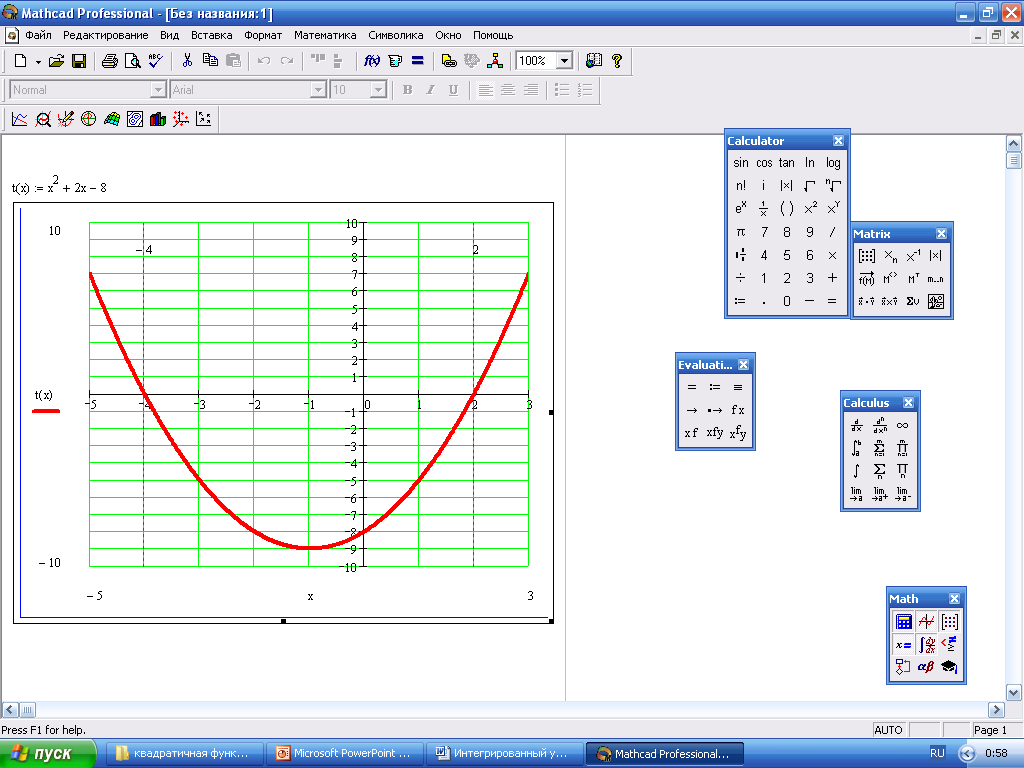
IV. Работа с программой MathCAD…

- За какой геометрической фигурой спрятан четвертый этап урока? /треугольник/. Вам предлагается решить графически неравенство х² + 2х – 3 > 5.

V. Тест.

И последняя геометрическая фигура – ромб приведет нас к пятому этапу урока, который включает в себя проверочный тест. Для прохождения теста откройте документ «Тест для 9 класса» в программе Excel.

Вариант I

1. Из функций: у = х² + 4, у = х – 3х² + 1, у = х⁶ -2х + 1, у = х – 1,у = (х + 1)² выберите квадратичные.

   • А) у = х² + 4, у = х – 3х² + 1;

   • Б) у = х² + 4, у = (х + 1)² ;

   • В) у = х² + 4, у = х – 3х² + 1, у = (х + 1)² ;

   • Г) у = х⁶ -2х + 1;

2. Найдите абсциссы точек пересечения параболы у = 4х² и прямой у = 3х + 1.

   • А) 0 и 3;

   • Б) 2 и -2;

   • В) ;

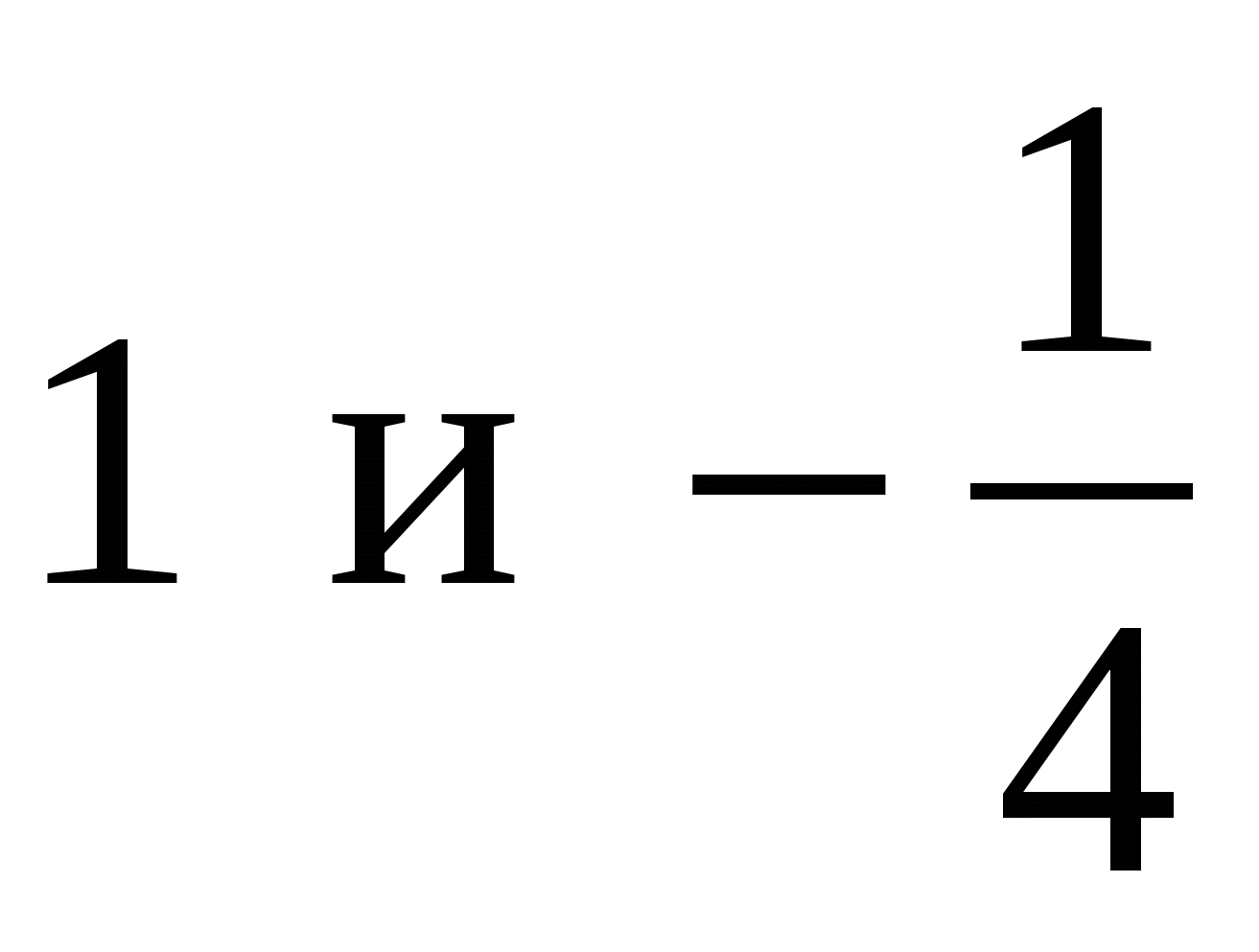   • Г) .

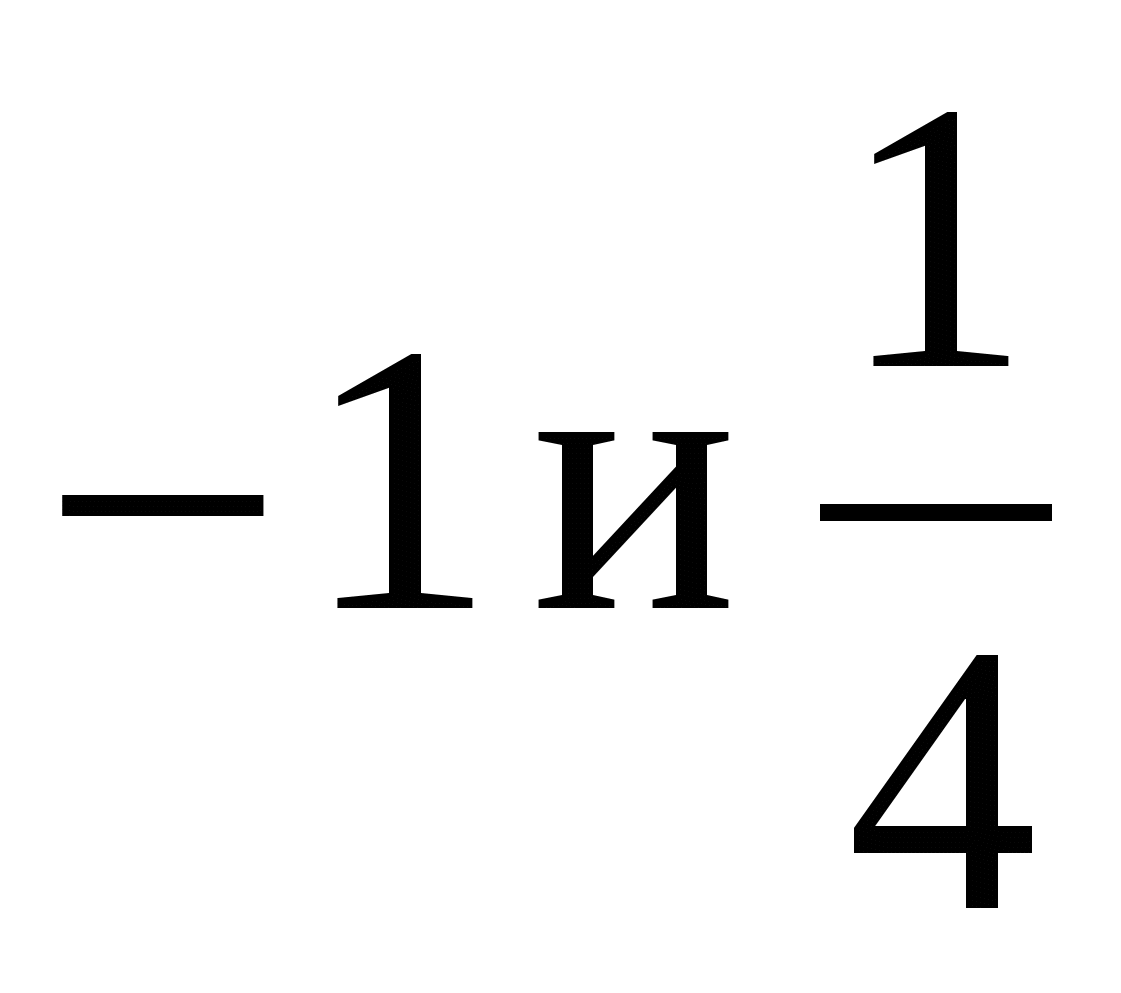3. Решите неравенство х² ≤ 121.

   • А) х

   • Б) х ≥ 11;

   • В) - 11 ≤ х ≤ 11;

   • Г) х ≤ 11, х > -11.

4. Найдите координаты вершины параболы у = - 6(х – 1)² .

   • А) (- 6; - 1);

   • Б) (1; 0);

   • В) (0; - 1);

   • Г) (1;0).

5. Найдите координаты точек пересечения параболы у = - 2х² + 8 с осью Ох.

   • А) (2;0);

   • Б) (0;0);

   • В) (0;4);

   • Г) (2;0), (-2;0).

6. Найдите координаты точек пересечения параболы у = х² + 10х - 11 с осью ординат.

   • А) (- 11;0);

   • Б) (0;- 11);

   • В) (0;0);

   • Г) (- 10; - 1).

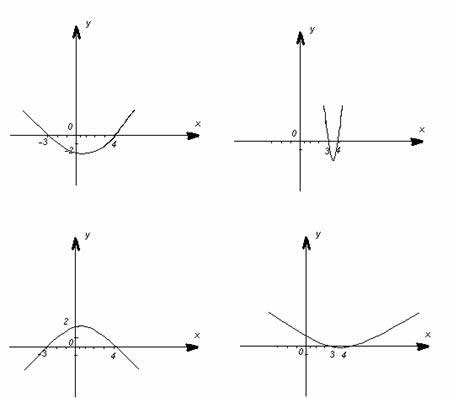
7. На каком из графиков изображена функция у = - х² + х + 12?

Для печатного теста можно предложить 2 варианта или подготовить 2 варианта в программе Excel.

Вариант 2

1. Из функций у = х² + 3х + 1, у = 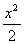+ 5, у = - х² + 3х, у = (х – 4)² + 5, у = х + 3х + 2,у = х⁴ – 6х выберите квадратичные.

   • А) у = х² + 3х + 1, у = х + 3х + 2;

   • Б) у = 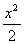+ 5, у = х² + 3х + 1;

   • В) у = х² + 3х + 1, у = - х² + 3х;

   • Г) у = х² + 3х + 1, у = 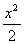+ 5, у = - х² + 3х, у = (х – 4)² + 5.

2. Найдите координаты точек пересечения параболы у = - х², и прямой у = 6х + 1.

   • А) (-5,8; 0,2);

   • Б) (≈5,8; 0,2);

   • В) (≈-0,2; ≈- 5,8);

   • Г) -0,2.

3. Решите неравенство х² ≥ 100.

   • А) х ≥ 10;

   • Б) - 10

   • В) - 10

   • Г) х

4. Найдите координаты вершины параболы = 2(х + 3)² – 5.

   • А) (3; -5);

   • Б) (3; 5);

   • В) (-3; -5);

   • Г) (-3; 5).

5. Найдите координаты точек пересечения параболы у = 3х² – 48 с осью абсцисс.

   • А) (0; 4);

   • Б) (4; 0), (-4; 0);

   • В) (4; 0), (0; 0);

   • Г) (4; 0).

6. Найдите координаты точки пересечения параболы у = х² +8х – 9 с осью Оу.

   • А) (0; -9);

   • Б)(0; 0);

   • В) (-9; 0);

   • Г) (9; -1).

7. На каком эскизе изображен график функции у = х² + 5х + 6?

VI. Итог урока. Д/з.

Фамилия, имя учащегося:

Тест по теме: Квадратичная функция

№ ЗАДАНИЯ

ВОПРОСЫ

ВАРИАНТЫ ОТВЕТОВ

1

Из функций: у = х^2 + 4, у = х – 3х^2 + 1, у = х^6 -2х + 1, у = х – 1,у = (х + 1)^2 выберите квадратичные.

2

Найдите абсциссы точек пересечения параболы у = 4х^2 и прямой у = 3х + 1

3

Решите неравенство х^2 ≤ 121

4

Найдите координаты вершины параболы у = - 6(х – 1)^2

5

Найдите координаты точек пересечения параболы у = - 2х^2 + 8 с осью Ох

6

Найдите координаты точек пересечения параболы у = х^2 + 10х - 11 с осью ординат

7

На каком из графиков изображена функция у = - х^2 + х + 12? (см. рисунок)

Результаты теста: