Конспект урока «Построение графиков функций, содержащих знак абсолютной величины» по алгебре для 9 класса

Урок алгебры в 9 классе.

Тема урока: «Построение графиков функций, содержащих знак абсолютной величины»

Цели урока:

1. 1. Обобщить теоретические знания по темам «Область определения и множество значений функции».

2. Отработать решение простейших задач на нахождение области определения функции.

3. Сформировать навыки построения графиков функций, содержащих знак абсолютной величины.

4. Организовать работу учащихся по указанным темам на уровне, соответствующем уровню уже сформированных знаний.

Ход урока

І этап урока - организационный (1 минута)

Учитель сообщает учащимся тему урока , цель и поясняет , что во время урока будет использоваться мультимедийное оборудование

ІІ этап урока (7 минут)

Проверка домашнего задания и повторение теоретического материала по темам

1. «Область определения функции»

2. «Множество значений функции».

3. «График функции»

Учитель обращается к учащимся с вопросом: «Дайте понятие области определения функции и сформулируйте правила её нахождения».

Возможные варианты ответа:

Если даны числовое множество X и правило f, позволяющее поставить в соответствие каждому элементу x из множества  X определенное число y, то говорят , что задана функция  y = f(x) с областью определения X : y = f(x), D(f) = X. 

Определение. Значения переменных, на которых задается функция  y = f(x) , называют допустимыми значениями переменных.

Определение. Значения переменных, при которых алгебраическое выражение P имеет смысл, называют допустимыми значениями переменных. Множество всех допустимых значений переменных называют областью допустимых значений переменных D(P).

Определение. Областью определения уравнения  f(x) = g(x) называют множество всех тех значений переменой x, при которых алгебраические выражения  f(x)  и  g(x) имеют смысл (одновременно).

Или:

Область определения и область значений функции. Аргумент функции может принимать только те действительные значения, при которых функция определена, т.e. она также принимает только действительные значения. Множество X всех допустимых действительных значений аргумента x, при которых функция y = f ( x ) определена, называется областью определения функции. Множество Y всех действительных значений y, которые принимает функция, называется областью значений функции. Теперь можно дать более точное определение функции: правило (закон) соответствия между множествами X и Y, по которому для каждого элемента из множества X можно найти один и только один элемент из множества Y, называется функцией.

ІІІ этап (8 минут).

Устная работа практической направленности (Работа по готовым чертежам с применением ИКТ).

Комментарии. Учитель готовит задания заранее в зависимости от оснащенности кабинета. Если кабинет не имеет технического оснащения, то нужно приготовить задания на доске или на листах бумаги и раздать их учащимся, если оснащен мультимедиатехникой, то нужно приготовить материал в режиме показа слайдов, если оснащен интерактивной доской, то приготовить задания для показа на доске и т.д.

IV этап (25 минут)

Объяснение нового материала «Построение графиков функций, содержащих знак абсолютной величины»

О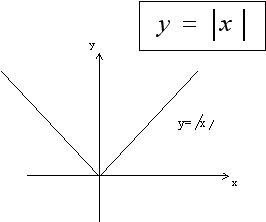пределение: Функция модуль является биссектрисами первого и второго координатных углов

Свойства:

• Функция модуль является четной функцией

• График функции модуль симметричен относительно оси ординат

Построение графиков вида:

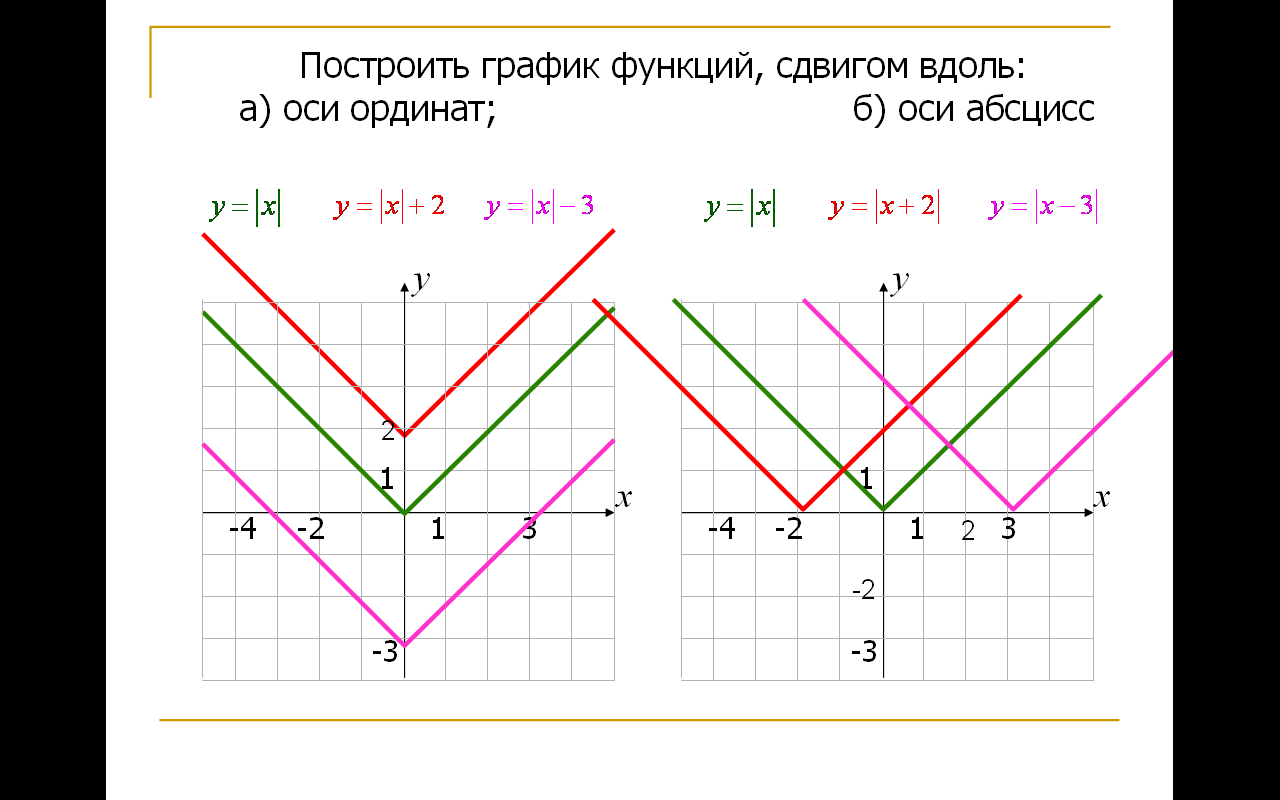
Построение графиков функций с помощью преобразования

Во многих случаях графики функций могут быть построены путем некоторых преобразований уже известных графиков других функций более простого вида. График функций вида:

может быть получен из графика функций при помощи следующих геометрических преобразований:

1. а) Осевой симметрии относительно оси абсцисс;

б) осевой симметрии относительно оси ординат;

в) центральной симметрии относительно начала координат;

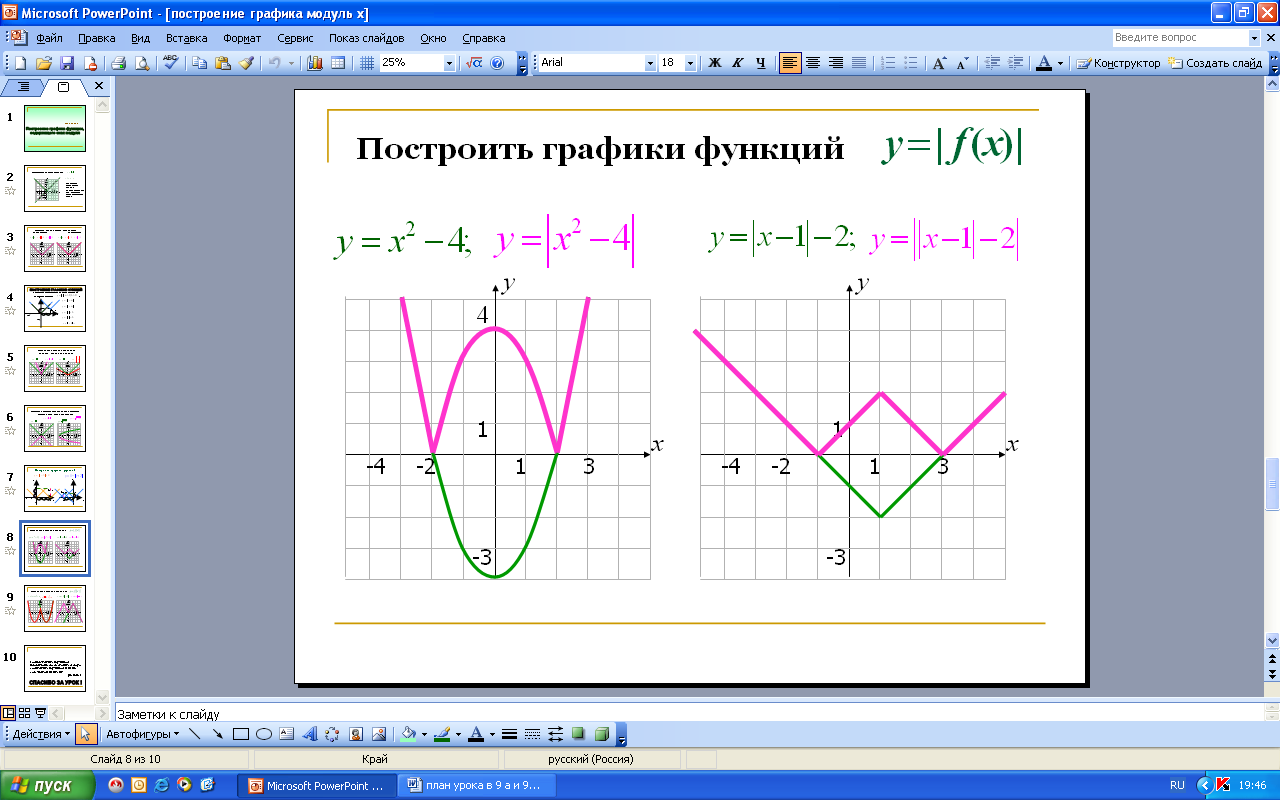
2. а) Параллельного переноса (сдвига) вдоль оси абсцисс;

б) параллельного переноса (сдвига) вдоль оси ординат;

3. а) Растяжения (или сжатия) по направлению оси абсцисс;

б) растяжения (или сжатия) по направлению оси ординат;

Отметим, что:

а) При осевой симметрии относительно оси абсцисс точка переходит в точку ;

б) При осевой симметрии относительно оси ординат точка переходит в точку ;

в) При центральной симметрии относительно начала координат переходит в точку

а) При параллельном переносе вдоль оси абсцисс точка переходит в точку где а – некоторое число при этом перенос происходит «вправо», если, и «влево», если

б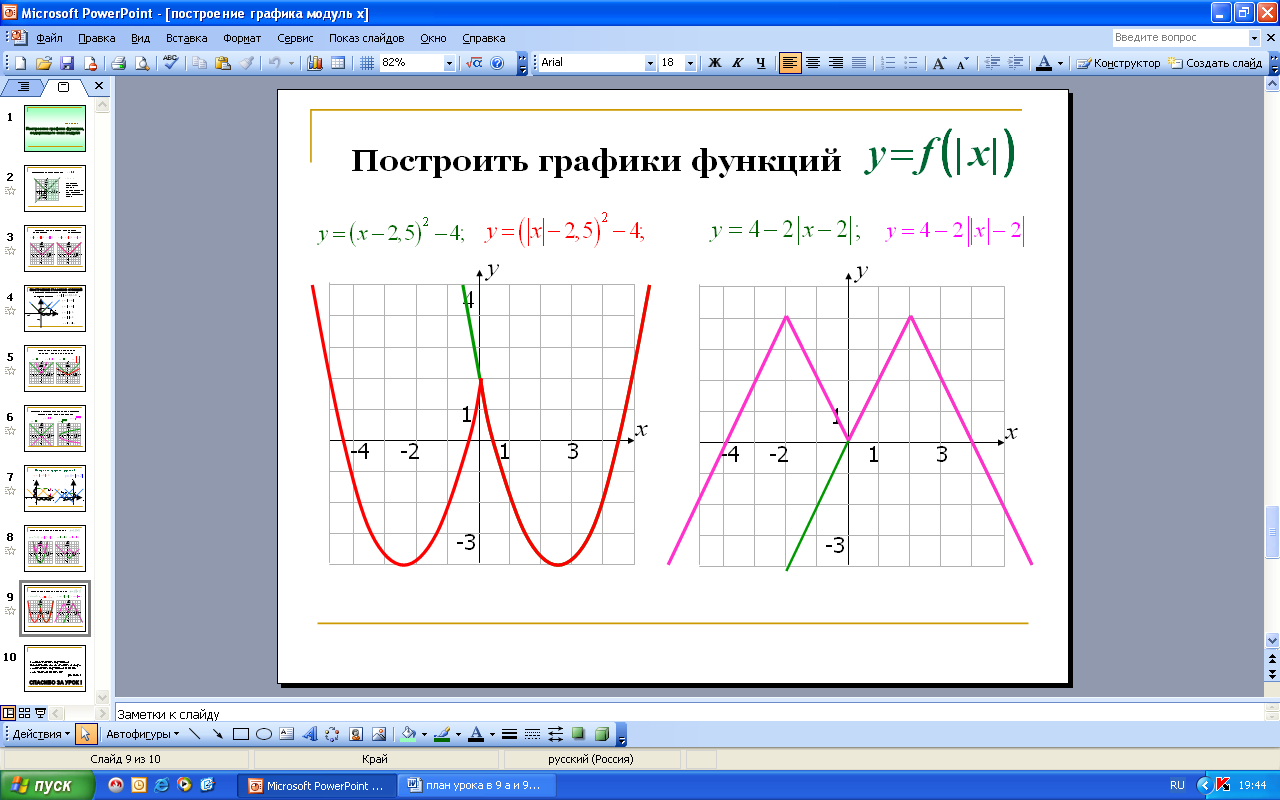) При параллельном переносе вдоль оси ординат точка переходит в точку , где b – некоторое число при этом перенос происходит «вверх», если и «вниз», если

3. а) При растяжении (сжатии) в k раз вдоль оси 0x относительно 0y точка переходит в точку.

б) При растяжении (сжатии) в q раз вдоль оси ординат относительно абсцисс точка переходит в точку .

Применительно к графикам функций эти свойства дают те конкретные геометрические преобразования (табл. 1), использование которых позволяет из известного графика функции строить графики других функций .

V этап урока (4 минут)

Подведение итогов урока, домашнее задание.

Комментарии. Учитель комментирует выставленные на уроке оценки. В качестве домашнего задания учащиеся получают:

1. §12, прочитать, выучить определения

2. № 162, № 164