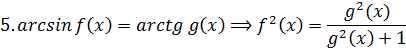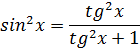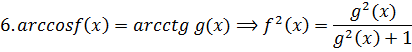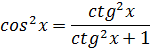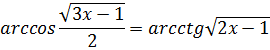Конспект урока «Методы решения уравнений и неравенств, содержащих обратные тригонометрические функции» по алгебре для 10 класса
Конспект урока по алгебре и началам анализа по теме
«Методы решения уравнений и неравенств, содержащих обратные тригонометрические функции»
Аннотация:
Урок алгебры и начала анализа в 10 классе физико – математического профиля. Цель урока: рассмотреть способы решения уравнений и неравенств, содержащих обратные тригонометрические функции и способствовать выработке навыков их решения. На уроке учащиеся анализируют различные методы решения уравнений и неравенств, содержащих обратные тригонометрические функции.
Автор: Макарова Татьяна Павловна, учитель математики ГБОУ СОШ №618 г. Москвы
Контингент: 10 класс физико-математического профиля.
Учебник: Алгебра и начала анализа. 10 кл. В 2 ч. Ч.1.Учебник для общеобразовательных учреждений (профильный уровень) / А.Г. Мордкович, П.В. Семенов. – М.: Мнемозина, 2012.
Уровень образования школьников: предпрофильный уровень
Цель урока:
-
Изучение способов решения уравнений и неравенств, содержащих обратные тригонометрические функции.
-
Решение более сложных типов уравнений и неравенств, содержащих обратные тригонометрические функции.
-
Развивать умение обобщать, правильно отбирать способы решения уравнений и неравенств, содержащих обратные тригонометрические функции.
-
Развивать самостоятельность, воспитывать грамотность речи.
Задачи урока:
1. Расширить и углубить представления учащихся о приемах и методах решения уравнений и неравенств, содержащих обратные тригонометрические функции.
2. Помочь овладеть рядом технических и интеллектуальных умений на уровне свободного их использования.
3. Развить интерес и положительную мотивацию изучения математики.
Тип урока: комбинированный.
Методы обучения: фронтальный, индивидуальный, групповой, наглядно-практический.
Формы организации совзаимодействия на уроке: учебная, групповая работа, индивидуальная работа
Педагогические средства: проблемные задания, работа с раздаточными материалами
Приобретаемые навыки детей: применение знаний к решению уравнений.
Продолжительность: 2 часа
Ход урока
-
Организационный момент
-
Усная работа в группах. Актуализация опорных знаний
Вспомним основные определения и свойства. Работа по группам.
1, 2, 3, 4 группы: рассказать об arcsin a, arccos a, arctg a, arcctg a . (Каждой группе в произвольном выборе достается одно из предложенных понятий).
Примерное время на подготовку ответов групп – 3 мин, после чего заслушиваются ответы.
Предполагаемые ответы групп:
-
Номер группы
Предполагаемый ответ
1
Функция
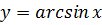 определена и монотонно возрастает на отрезке [- 1; 1];
определена и монотонно возрастает на отрезке [- 1; 1];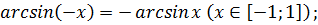
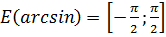 .
.2
Функция
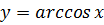 определена и монотонно убывает на отрезке [- 1; 1];
определена и монотонно убывает на отрезке [- 1; 1];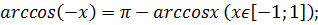
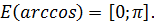
3
Функция
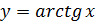 определена и монотонно возрастает на R;
определена и монотонно возрастает на R;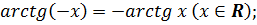
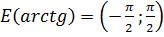 .
.4
Функция
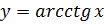 определена и монотонно убывает на R;
определена и монотонно убывает на R;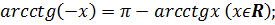
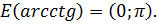
-
Актуализация опорных знаний
Вспомним важнейшие свойства обратных тригонометрических функций.
![]() ;
;
![]()
![]()
-
Изучение нового материала.
Свойства монотонности и ограниченности являются ключевыми при решении многих уравнений и неравенств, содержащих обратные тригонометрические функции. Перейдем к рассмотрению методов решения этих уравнений и неравенств.
-
Метод замены переменных.
Пример 1. Решите уравнение: ![]()
Решение. Для новой переменной ![]() исходное уравнение примет вид:
исходное уравнение примет вид: ![]()
![]()
![]()
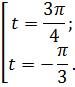
Замечаем, что ![]() не удовлетворяет условию
не удовлетворяет условию ![]() .
.
Следовательно, ![]()
Ответ: ![]()
-
Уравнения и неравенства, левая и правая части которых являются одноименными обратными тригонометрическими функциями
Решение уравнений и неравенств, левая и правая части которых являются одноименными обратными тригонометрическими функциями различных аргументов, основывается на свойстве монотонности этих функций. Поэтому справедливы следующие равносильные переходы.
1). ![]()
2). ![]()
3). ![]()
4). ![]()
5). 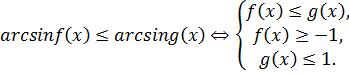
6).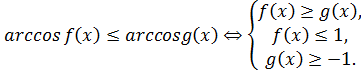
7).![]()
8).![]()
Пример 2. Решите уравнение: ![]()
Решение. Уравнение равносильно системе
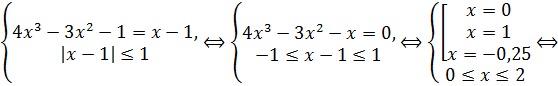
![]()
Ответ: 0; 1.
-
Уравнения и неравенства, левая и правая части которых являются разноименными обратными тригонометрическими функциями
При решении уравнений и неравенств, левая и правая части которых являются разноименными обратными тригонометрическими функциями различных аргументов, пользуются известными тригонометрическими тождествами.
| Использована формула | |
| 1. |
|
| 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Корнем каждого из уравнений (1) – (4) может быть только такое число х, для которого ![]() В противном случае множество значений левой и правой частей уравнения не пересекаются.
В противном случае множество значений левой и правой частей уравнения не пересекаются.
Пример 3. Решите уравнение ![]()
Решение.![]()
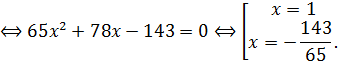
Корень ![]() является посторонним.
является посторонним.
Ответ: 1.
-
Уравнения и неравенства, сводимые к алгебраическим и тригонометрическим уравнениям и неравенствам
Пример 4. Решите уравнение ![]()
Решение. Пусть ![]() Тогда
Тогда ![]()
![]()
Пусть ![]() Тогда
Тогда ![]()
![]()
Тогда исходное уравнение примет вид ![]()
Тогда ![]()
Поэтому
![]()
Ответ: 0; 1.
-
Работа в группах
| Задание . Решите уравнения: | ||
| Группа 1 | №1 |
|
| №2 |
| |
| №3 |
| |
| №4 |
| |
| №5 |
| |
| Группа 2 | №1 |
|
| №2 |
| |
| №3 |
| |
| №4 |
| |
| №5 |
| |
| Группа 3 |
|
|
| №2 |
| |
| №3 |
| |
| №4 |
| |
| №5 |
| |
| Группа 4 |
|
|
| №2 |
| |
| №3 |
| |
| №4 |
| |
| №5 |
|
Ключи
| Ответы | ||
| Группа 1 | №1. |
|
| №2 | | |
| №3 |
| |
| №4 |
| |
| №5 |
| |
| Группа 2 | №1. |
|
| №2 |
| |
| №3 |
| |
| №4 |
| |
| №5 |
| |
| Группа 3 | №1. |
|
| №2 |
| |
| №3 |
| |
| №4 |
| |
| №5 |
| |
| Группа 4 | №1. |
|
| №2 |
| |
| №3 |
| |
| №4 |
| |
| №5 |
|
-
Письменная самостоятельная работа
| Вариант 2 | |||
| Решите уравнения: | |||
| 1 |
| 1 |
|
| 2 |
| 2 |
|
| 3 |
| 3 |
|
| 4 |
| 4 |
|
| 5 |
| 5 |
|
Ключи
| Вариант 2 | |||
| 1 |
| 1 |
|
| 2 |
| 2 |
|
| 3 |
| 3 |
|
| 4 |
| 4 |
|
| 5 |
| 5 |
|
-
Итоги урока.
-
Деятельность учителя
Деятельность учащихся
Дает анализ и оценку успешности достижения цели и намечает перспективу последующей работы. Задает домашнее задание.
Получают информацию о результатах самостоятельной работы. Записывают домашнее задание.
-
Рефлексия
-
Деятельность учителя
Деятельность учащихся
Учитель, побуждает высказаться учащихся о том понравился ли им урок, что они узнали нового, смогут ли применить полученные знания.
Осмысливают свою деятельность на уроке, проводят самооценку своей деятельности
-
Домашняя работа
Алгебра и начала анализа. 10 кл. В 2 ч. Ч. 2. Задачник для общеобразовательных учреждений (профильный уровень) / А.Г. Мордкович, П.В. Семенов. – М.: Мнемозина, 2012.
Решить задания №№21.58, 21.59,21.62.
Список используемой литературы
-
Алгебра и начала анализа. 10 кл. В 2 ч. Учебник для общеобразовательных учреждений (профильный уровень) / А.Г. Мордкович, П.В. Семенов. – М.: Мнемозина, 2012.
-
Алгебра и начала анализа. 10 кл. В 2 ч. Ч. 2. Задачник для общеобразовательных учреждений (профильный уровень) / А.Г. Мордкович, П.В. Семенов. – М.: Мнемозина, 2012.
-
Фалин Г.И. Обратные тригонометрические функции. 10 – 11 классы/ Г.И. Фалин, А.И. Фалин. – М.: Экзамен, 2012.
-
Шестаков С., Галицкий М. Уравнения и неравенства, содержащие обратные тригонометрические функции.- Математика №13,14, 2000 г.
-
Шабунин М.И. Математика. Алгебра. Начала математического анализа. Профильный уровень: учебник для 10 класса/ М.И. Шабунин, Прокофьев А.А. – М.:БИНОМ, 2007.
Макарова Т.П., учитель математики ГБОУ СОШ №618 Страница
Здесь представлен конспект к уроку на тему «Методы решения уравнений и неравенств, содержащих обратные тригонометрические функции», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (10 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.