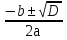Конспект урока «Квадратные уравнения» по алгебре для 8 класса
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа №1 имени Н.Л. Мещерякова
г. Зарайск
Конспект урока
в 8 классе
«Квадратные уравнения»
Подготовила учитель математики
первой квалификационной
категории
Авдюхина Л.А.
2012-2013 учебный год
ЦЕЛЬ УРОКА: систематизировать и обобщить знания учащихся по теме
«Квадратные уравнения».
ЗАДАЧИ:
-
выявить уровень овладения умениями решать квадратные уравнения; контроль усвоения знаний и умений;
-
развитие вычислительных навыков, речи, внимания, математического и общего кругозора; формирование и развитие умения мыслить и анализировать.
-
воспитание интереса к математике, активности, самостоятельности; воспитание умения выдерживать регламент времени, отведенного на решение каждого задания.
ТИП УРОКА: урок обобщения и систематизации
ТЕХНОЛОГИИ ОБУЧЕНИЯ: личностно-ориентированная, элементы игровой технологии, технология уровневой дифференциации.
ФОРМЫ РАБОТЫ: парная, индивидуальная
ОБОРУДОВАНИЕ: карточка-лото, карточка «Меткие стрелки»
СТРУКТУРА УРОКА:
-
Организационный момент и постановка цели урока.
-
Актуализация ранее изученного: теоретический опрос.
-
Основной этап: выполнение специально подобранных заданий, контроль и оценка результатов.
-
Итог урока и сообщение домашнего задания.
ХОД УРОКА
-
Организационный момент и постановка цели урока.
Цель: формирование мотива работать на уроке.
а) Организационное начало
Учитель:
Начать урок я хочу словами: «Только упорство, труд, настойчивость в любом деле приносят свои результаты». Сегодня у нас обобщающий урок по теме «Квадратные уравнения». Ваша задача – показать свои знания, умения и навыки по данной теме.
Посмотрите друг на друга, улыбнитесь! Я желаю вам сегодня на уроке удачи, точных расчетов и вычислений, новых открытий.
б) Психологическая установка на работу.
Учитель:
Сядьте удобно, закройте глаза. Повторяйте за мной:
-
Я в школе на уроке.
-
Сейчас я начну учиться.
-
Я радуюсь этому.
-
Память моя крепка.
-
Я готов к работе.
-
Я работаю!!
-2-
2) Актуализация ранее изученного: теоретический опрос.
Цель: повторение ключевых знаний; развитие умения слушать.
Учитель:
Сейчас каждая пара получит карту и набор кружков, которые по размеру помещаются в клетку карты. На одной стороне кружка написаны номера, соответствующие номеру вопроса. В клетках карты написаны ответы на вопросы. Я называю номер вопроса и сам вопрос. Вы отвечаете про себя на вопрос, ищите ответ в своих картах и закрываете кружком с номером, соответствующим номеру вопроса.
ВОПРОСЫ:
-
Квадратным уравнением называется…..
-
Неполным квадратным уравнением называется….
-
При решении квадратного уравнения целесообразно поступать следующим образом…
-
Формула корней квадратного уравнения….
-
Приведенным квадратным уравнением называется….
-
При решении дробных рациональных уравнений поступают следующим образом…
-
Дискриминантом квадратного уравнения называют…
КАРТА
| 1.вычислить дискриминант и сравнить его с нулем. 2.если D≥o, то воспользоваться формулой корней; если D | ||||
| квадратное уравнение, в котором первый коэффициент равен 1 | 1.Найти общий знаменатель дробей, входящих в уравнение 2.умножить обе части уравнения на общий знаменатель 3.решить получившееся целое уравнение 4.исключить из его корней те, которые обращают в нуль общий знаменатель | Уравнение вида ax2 + bx +c=0, где х- переменная, a,b,c –некоторые числа, причем a≠0 | ||
| квадратное уравнение, в котором хотя бы один из коэффициентов b или c равен нулю | Х= | |||
После выполнения идет фронтальная проверка.
3)Основной этап.
Цель: закрепление и совершенствование навыков решения квадратных уравнений.
а) Устная работа
Закончите предложения так, чтобы оно было верным:
-
Если D > 0, то…
-
Если D = 0, то…
-
Сумма корней приведенного квадратного уравнения …..
-
Если D
-
Произведение корней приведенного квадратного уравнения…
б) Диктант (работа на листочках под копирку).
Учитель:
На доске записаны уравнения, у каждого свой номер. Слушаем вопрос и отвечаем на него, записав в ответе номер уравнения.
-3-
1) 49 = 14х + 2х2;
2) х2 – 4х = 5;
3) 2х2 – 8 = 0;
4) (х – 2) х =0;
5) х2 – 9 = 0;
6) 35х2 + 2х -1 = 0;
7) х – 5 =0
Вопросы
а) Среди уравнений укажите номера тех, которые являются (записать в ответе номер уравнения):
1) полными квадратными уравнениями;
2) приведенными квадратными уравнениями;
3) неполными квадратными уравнениями.
б) В уравнении №5 запишите значения коэффициентов a, b, c
в) Найдите сумму и произведение корней в уравнении №5.
г) Решите уравнение №6
После выполнения один лист сдают учителю, а по второму идет фронтальная проверка.
в) Кубик – экзаменатор
Учитель:
Чтобы решить уравнение,
Корни его отыскать.
Нужно немного терпения,
Ручку, перо и тетрадь.
Уравнения записаны на гранях кубика. Ученик выходит к доске, подкидывает кубик и решает уравнение, которое выпало на грани на доске с полным объяснением; остальные учащиеся работают в тетрадях с этим же уравнением.
(х-4) (х+4) = -2х + 64;
(х + 1)2 = 9;
5х2 - 3х = 0;
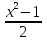 = 11 = 11х;
= 11 = 11х;
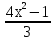 = х(10х-9)
= х(10х-9)
г) Проверочная самостоятельная работа.
Цель: контроль усвоения изученного материала
Учитель: Хорошо. Вместе мы поработали. Теперь посмотрим, как вы умеете работать самостоятельно. Вам предлагается трехуровневая работа. Если вы еще не уверены в своих силах и желаете закрепить решение уравнение, то выбираете уровень А (1 балл за задание). Если считаете, что материал усвоен хорошо – уровень В (2 балла за задание). Ну, а если желаете испробовать свои
-4-
силы на более сложных заданиях – уровень С (3 балла за задание) для вас. В процессе решения я проверяю ваши работы и проставляю заработанные баллы.
Вариант 1.
Уровень А
№1. Для каждого уравнения вида ax2 + bx + c = 0 укажите значения a, b, c.
а) 3х2 + 6х – 6 = 0, б) х2 - 4х + 4 = 0
№2. Продолжите вычисление дискриминанта D квадратного уравнения ax2 + bx + c = 0 по формуле D = b2 - 4ac.
5х2 - 7х + 2 = 0, D = b2 - 4ac = (-7)2 – 4· 5 · 2 = …;
№3. Закончите решение уравнения 3х2 - 5х – 2 = 0.
D = b2 - 4ac = (-5)2- 4· 3·(-2) = 49; х1 = … х2=…
Уровень В Решите уравнение: а) 6х2 – 4х + 32 = 0; б) х2 + 5х - 6 = 0.
Уровень С
Решите уравнение: а) -5х2 – 4х + 28 = 0; б) 2х2–8х–2=0.
Доп. задание. При каком значении а уравнение х2 - 2ах + 3 = 0 имеет один корень?
Вариант 2.
Уровень А
№1. Для каждого уравнения вида ax2 + bx + c = 0 укажите значения a, b, c.
а) 4х2 - 8х + 6 = 0, б) х2 + 2х - 4 = 0
№2. Продолжите вычисление дискриминанта D квадратного уравнения ax2 + bx + c = 0 по формуле D = b2 - 4ac.
5х2 + 8х - 4 = 0, D = b2 - 4ac = 82 – 4· 5 · (- 4) = …;
№3. Закончите решение уравнения х2 - 6х + 5 = 0.
D = b2 - 4ac = (-6 )2 - 4· 1·5 = 16; х1 = … х2=…
Уровень В Решите уравнение: а) 3х2 – 2х + 16 = 0; б) 3х2 - 5х + 2 = 0.
Уровень С
Решите уравнение: а) 5х2 + 4х - 28 = 0; б) х2 – 6х + 7 = 0;
Доп.задание. При каком значении а уравнение х2 + 3ах + а = 0 имеет один корень.
4)Итог урока и сообщение домашнего задания.
Учитель:
Итак, мы проделали большую работу. Повторили всю теорию, прорешали различные виды уравнений как вместе, так и вы сами. Настало время подвести итог.
-
Рефлексия.
Кто может сказать: “Да, я умею решать квадратные уравнения!”
Поставьте оценку работе всего класса за работу на уроке, можно с комментариями.
-
Сообщение домашнего задания.
-
Ребята, а у меня для вас есть сюрприз, который я спрятала в классе. Для того чтобы узнать, где он находится, надо решить следующее задание:
-5-
В уравнении х2 - рх + 3 = 0 один из корней равен 3. Если вы найдете число р, то узнаете номер парты, а второй корень укажет ряд, на котором находится парта с сюрпризом. (р = 4, х = 1)
Сюрприз: конверт, на котором надпись "Спасибо за урок!!! Вы замечательно поработали»
-6-
Литература
1.М.Р. Леонтьева, С.Б. Суворова. Упражнения в обучении алгебре. Книга для
учителя. Москва «Просвещение» 1985.
2. Л.В. Кузнецова, С.С. Минаева, Л.О. Рослова. Алгебра. Контрольные работы
7-9 классы. Пособие для учителей общеобразовательных учреждений.
Москва «Просвещение» 2010.
-7-
Здесь представлен конспект к уроку на тему «Квадратные уравнения», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (8 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.