Конспект урока «Квадратные уравнения» по алгебре для 9 класса
Муниципальное бюджетное общеобразовательное
учреждение «Владимирская ООШ»
МО Енотаевский район
Конспект урока по алгебре
в 9 классе по теме:
«Квадратные уравнения»
подготовила
учитель математики и физики
Каталиева Жамиля Лазаревна
с. Владимировка
Цель :- формирование толерантности у детей, одним из проявлений которой
является «уважение к разнообразию различных мировых культур,
цивилизаций и народов.
- готовность к пониманию и сотрудничеству с людьми.
- познакомить учеников с фрагментами истории математики на уроках
алгебры.
Ход урока
-
Физкультминутка-2мин.
-
Организационный момент (карта)
Вступительное слово учителя.
-
Проверка домашнего задания – молчаливый зачёт
-
Буквенный диктант (толерантность)
Ребят, давайте представим себе, что с помощью фантастической машины времени и пространства мы очутились в городе, который населяют представители различных цивилизаций: Древнего Египта, Древнего Вавилона, Древней Греции, Древнего Китая, Древней Индии. Представим, что все мы - дети разных времён и народов – едины в одном стремлении: овладеть приёмами решения уравнений (квадратных). Разделим наш город на кварталы и представителю каждого дадим слово. Итак , слово Древнему Египту.
Древний Египет
Представитель Египтян
Впервые квадратные уравнения сумели решить математику Древнего Египта. В одном из математических папирусов содержится задача:
Найти стороны поля имеющего форму прямоугольника если его S=12, а 3/4длины равны ширине.
Пусть х- длина, тогда 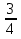 х –ширина
х –ширина
12=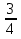 х2
х2 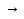 х2 = 12*
х2 = 12* 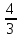 = 16 х=4
= 16 х=4
Ответ: 4м; 3м
Прошли тысячелетия в алгебру вошли (-) числа. х2 =16  х=
х= 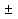 4
4
х=4 т.к длина должна быть (+). Слово представителям «вавилонского квартала».
Древний Вавилон
Представитель вавилонян
Огромный шаг вперёд по сравнению с математиками Египта сделали
учёные Междуречья.
Они нашли правило для решения приведённого квадратные уравнения.
х2 +рх+д=0, где р и д – v действительные числа.
В одной из вавилонских задач так же требовалось определить длину прямоугольного поля.
Пусть х- длина, тогда у-ширина
Сложив длину и две ширины прямоугольного поля получишь 14, а площадь поля 24. Найти его стороны
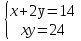
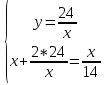 х2-14х+48=0
х2-14х+48=0
(х2-2*7х+49)-49+48=0
(х2-2*7х+49)=1
(х-7)=1
х-7=1 или х-7=-1
х=8 х=6
у=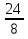 =3 у=
=3 у=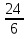 =4
=4
Ответ (8:3) или (6:4)
Древняя Греция
Представители греческого квартала.
Я расскажу вам, как составлял и решал квадратные уравнения греческий математик Диофант. При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.
Зад. Найти два числа, зная, что их сумма равна 20, а произведение 96
Диофант рассуждает так.
(10+х)-1число, (10-х)-2число
10+х+10-х=20
(10+х)(10-х)=96
100-х2=96
4=х2 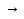 х=
х=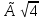 х1=2 х2=-2
х1=2 х2=-2
(10+2)=12
(10-2)=8
Задачи на составление квадратных уравнений встречаются уже в астрономическом трактате «Ариабхатиам»,
составленном в 499г, индийским математиком и астрономом Ариабхаттой. Индийский учёный Брахмагупта (7в) изложил общее правило решения квадратных уравнений вида ах2+вх=с
Древняя Индия.
Представитель индийского квартала.
Устный счёт:
Знаете в Древней Индии были распространены публичные соревнования в решении трудных задач. Приведу одну из задач знаменитого индийского математика 12века. Бхаскары.
Обезьянок резвых стая
Всласть поевши, развлекалась.
Их в квадрате часть восьмая
На поляне забавлялась
А 12 по лианам
Стали прыгать, повисая,
Сколько ж было обезьянок,
Ты скажи мне, в этой стае?
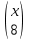 2+
2+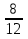 =х
=х 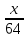 2 +
2 +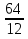 =
=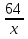
х2- 64х+768=0
х2-64х+322=-768+1024
(х2-32)2=256
х-32=16 или х-32=-16
х1=48
х2=16
Огромный вклад в развитие математики внесли учёные Древнего Китая
Представитель китайского квартала
Во 2в. До н.э. была написана «математика в девяти книгах»
Позднее, в 7 веке, она вошла в сборник « десять классических трактатов», который изучали в течение многих столетий, где объясняется, как извлечь 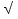 с помощью формулы квадрата суммы двух чисел.
с помощью формулы квадрата суммы двух чисел.
Метод получил название «тянь-юань» (буквально-небесный элемент»)-так китайцы обозначали неизвестную величину.
Обратим свои взоры к Средневековому востоку. 9-12в. – это расцвет науки в арабоязычных странах. Арабский язык стал языком науки.
Слово аль-джебр- книга о восстановлении и противопоставлении со временем превратилось в хорошо знакомое слово «алгебра»
Представитель «европейского» квартала
Формулы решения квадратных уравнений по образцу аль-хорезми в Европе были впервые изложены в книге абака 1202г., итальянским математиком Леонардо Фибоначчи.
Общее правило решения квадратных уравнений, при ведённых к единому каноническому виду х2+вх=с
При всевозможных комбинациях знаков коэффициентов в и с сформулировано в Европе лишь в 1544г. Штифелем.
Лишь в 17в. Благодаря трудам Жирара, Декарта, Ньютона и других учёных, способ решения квадратных уравнений принимает современный вид.
Учитель Перейдём теперь к практической части урока.
Обратимся к квадратным уравнениям.
х2+х=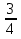
Являясь современными учениками 9 класса, обладая запасом знаний, накопленным нашими предками, какими способами мы можем решить это уравнение?
-
х2+х=
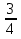
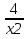 +
+ 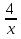 =
=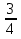
4х2+4х-3=0
Д=16+48=64
х1,2=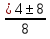
х1=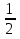 , х2=-1,5
, х2=-1,5
2.Учитывая чётность второго коэффициента
4х2+4х-3=0 4х2+2*2х-3=0
Д=к2-ас
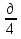 =4+4*3=16
=4+4*3=16
х=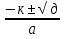
х=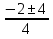
х1=-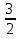 =-1,5 х2=
=-1,5 х2=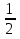
3. х2+х-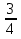 =0
=0
х2+2*х*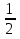 +
+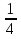 -
-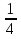 -
- 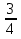 =0
=0
(х+ 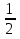 )2 - 1=0 х+
)2 - 1=0 х+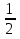 = 1 или х+
= 1 или х+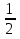 = -1
= -1
х=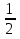 х= -1 -
х= -1 - 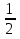 = - 1
= - 1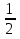
4.П-им график функции у=х2+х-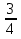
1)Графиком является парабола, ветви который направлены вверх, т.к. а =1>0
2) Координаты вершины
m = - 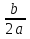 m = -
m = - 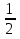
n= (-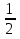 )2 -
)2 - 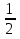 -
- 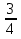 =
=
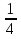 -
- 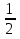 -
- 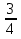 =
= 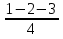 = -1
= -1
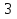 ) Составим таблицу.
) Составим таблицу.
| -2 | -1 | - | 0 | 1 | |
| у | 1 | - | -1 | - | 1 |
Итог урока:
-Во первых, мы сделали то, о чём в своё время говорил У. Сойер: «Человеку, изучающему алгебру, что полезнее решать одну и ту же задачу тремя различными способами, чем решать 3-4 различные задачи.
Решая одну задачу различными методами, можно путём сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт.
Во-вторых, ещё раз убедились в том, насколько велика роль науки, в частности математики, в развитии человеческого общества, ведь для науки нет понятий границ, наций и эпох.
Список использованной литературы:
-
Газета Математика
-
Учебник: Алгебра. 9 класс. Ю.Н. Макарычев, Н. Г. Миндюк и др. под редакцией С.А. Теляковского.
-
Методическое пособие: Ершова А.П., Голобородько В.В., Ершова А.С. Самостоятельные и контрольные работы по алгебре для 9 класса. – М.: Илекса, – 2007.
-
Учебник История древнего мира.
-
3.Ван дер Варден Б.Л. Алгебра – СПб.: Лань, 2004. – 624с.
-
Наглядность
Здесь представлен конспект к уроку на тему «Квадратные уравнения», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (9 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

