Конспект урока «Решение сложных иррациональных уравнений и систем, содержащих иррациональные уравнения» по алгебре для 11 класса
Болявина Наталья Сергеевна
Учитель математики
ГБОУ СОШ № 756 г. Москвы
Разработка урока по алгебре и началам анализа в 11 классе
(профильный уровень)
Тема: «Решение сложных иррациональных уравнений и систем, содержащих иррациональные уравнения».
Цель урока: формирование умений и навыков решения сложных иррациональных уравнений и систем, содержащих иррациональные уравнения.
Ход урока.
-
Организационный момент (1 минута).
-
Проверка домашнего задания (3 минуты).
Цель: актуализация знаний. Ответы и решение сложного уравнения выписаны на доске.
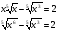
Обозначим 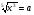
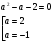
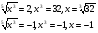
Ответ: 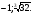
-
Решение задач (15 минут).
Рассмотреть условия равенства нулю произведения двух сомножителей.
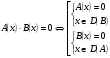
Пример 1. Решить уравнение 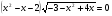 .
.
Решение.
Разложим на множители.
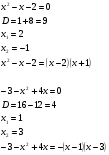
Найдём область определения выражения
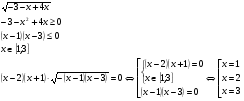 .
.
Ответ: 1;2;3.
Пример 2. Решить уравнение 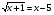 графическим способом.
графическим способом.
Решение.
Иногда при решении иррационального уравнения полезно использовать графики. Построим в одной системе координат графики функций 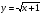 и
и 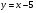
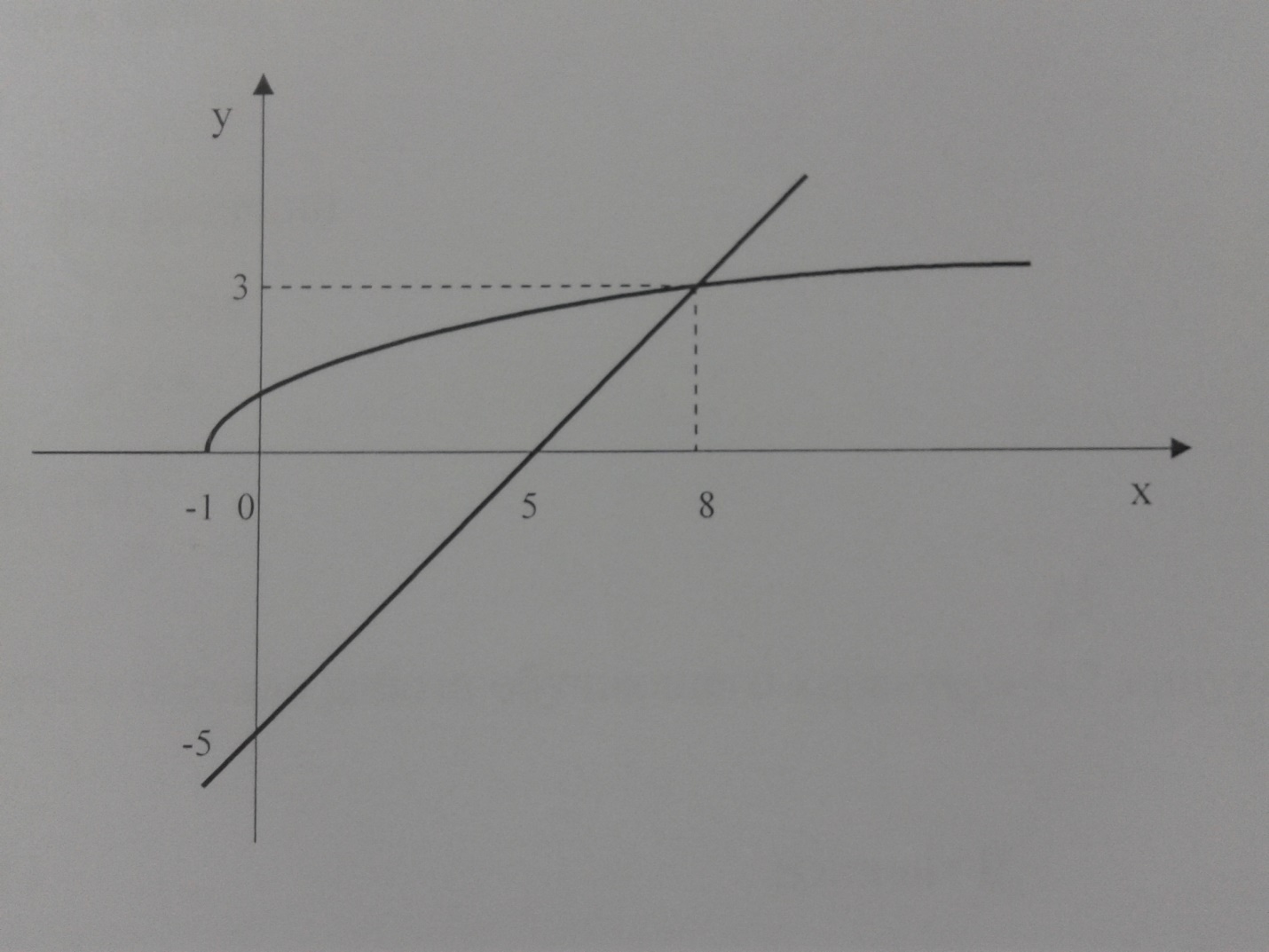
Графики пересекаются в точке 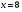 .
.
Ответ: 6.
Пример 3. Решить систему уравнений 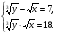
Решение.
Замена: 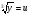 ,
, 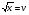 .
.
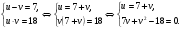
Решим второе уравнение.
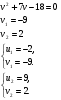
Вернёмся к замене.
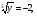
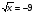 - нет решений.
- нет решений.
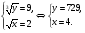
Ответ: 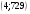 .
.
Пример 4. Решить систему уравнений.
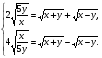
Решение.
Применим метод умножения.
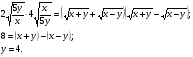
Подставив значение 4 вместо y во второе уравнение исходной системы, получим иррациональное уравнение с одной переменной:
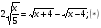
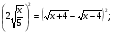
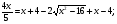
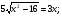
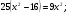
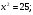
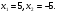
Значение -5 не удовлетворяет уравнению (*), значение 5 – удовлетворяет. Получили x=5, y=4. Проверка подстановкой найденных значений в исходную систему убеждает нас в том, что пара (5;4) – решение заданной системы.
Ответ: (5;4).
IV. Самостоятельная работа обучающего характера (12 минут).
| Вариант II. а) б) в) | Вариант II. а) б) в) |
Решение самостоятельной работы (ВариантII).
а)
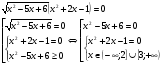
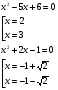
Ответ: 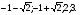
б)
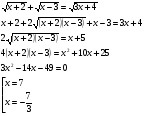
Проверка:
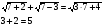
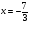 не является корнем уравнения, т.к. выражение
не является корнем уравнения, т.к. выражение 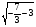 не имеет смысла.
не имеет смысла.
Ответ: 7.
в)
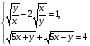
Обозначим 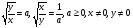
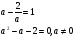
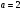
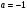 не удовлетворяет условию
не удовлетворяет условию 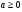
Вернемся к обозначениям:
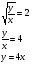
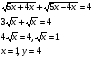
Ответ: (1;4).
-
Анализ результатов самостоятельной работы (10 минут).
Проверка правильности решений на доске. Анализ типичных ошибок, допущенных учащимися.
-
Итог урока. Выставление оценок за самостоятельную работу (2 минуты).
-
Домашнее задание. Инструктаж по домашнему заданию (2 минуты).
Решить систему уравнений.
а) 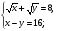
б) 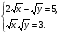
Решить уравнение:
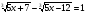 .
.
Список использованных источников информации:
-
Виленкин Н.Я., Сурвилло Г.С. и др. Алгебра. 9 класс. С углубленным изучением математики: учебник. – 7-е изд. - М.: Просвещение, 2006. - 368 с.
-
Колмогоров А.Н. и др. Алгебра и начала математического анализа. 10-11 классы: учебник. – 17-е изд. - М.: Просвещение, 2008. - 384 с.
-
Мордкович А.Г. и др. Алгебра и начала математического анализа. 11 класс. Профильный уровень: учебник. – 3-е изд., стер. - М.: Мнемозина, 2009. - 264 с.
-
Мордкович А. Г. Алгебра. Углубленное изучение. 9 касс: учебник. – 2-е изд., стер. – М.: Мнемозина, 2006. – 296 с.
Здесь представлен конспект к уроку на тему «Решение сложных иррациональных уравнений и систем, содержащих иррациональные уравнения», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (11 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

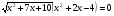 ;
;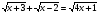 ;
;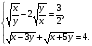
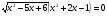 ;
;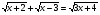 ;
;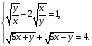
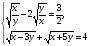 .
.