Конспект урока «Решение иррациональных уравнений» по алгебре для 9 класса
Муниципальное общеобразовательное учреждение
средняя общеобразовательная школа № 31
города Мурманска
Конспект урока
«Решение иррациональных уравнений»
Преподавание по учебнику
«Алгебра 9 для классов с углублённым изучением математики»
Авторы: Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков
Автор урока: Иванова Татьяна Ивановна,
МОУ СОШ № 31 г. Мурманска
Тема урока: «Решение иррациональных уравнений»
9 класс углублённого изучения математики
| Урок комплексного применения знаний и способов действий учащихся | |
| Цель занятия: |
|
| Форма занятия: | Урок-семинар |
| Логика занятия: | Мотивация – актуализация комплекса знаний необходимых для их применения на творческом уровне – самостоятельное выполнение заданий на творческом уровне – проверка – анализ – оценка – коррекция. |
| Технология занятия: | Традиционное обучение в сочетании с ИКТ и элементами технологии личностно ориентированного развивающего обучения. |
Содержание знаний и способов действий:
Основные методы решения уравнений и систем, содержащих радикалы: возведение в степень; метод подстановки; применение свойств функций к решению уравнений и использование монотонности функции при решении уравнений;
Уровни и показатели степени обученности:
-
различение;
-
понимание;
-
запоминание;
-
элементарные умения и навыки;
-
применение ЗУН для решения нестандартных задач (высшие умения и навыки).
| Мне приходится делить свое время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее потому, что политика существует только для данного момента, а уравнения будут существовать вечно. А. Эйнштейн Что означает владение математикой? Это есть умение решать задачи, притом не только стандартные, но и требующие известной независимости мышления, здравого смысла, оригинальности, изобретательности. Д. Пойа |
Ход урока.
I. Организация начала занятий.
Класс разбит на 3 творческие группы (по рядам). Каждая группа предварительно получила задание с уравнениями, которые необходимо было решить дома, применяя интенсивную работу с учебниками, пособиями, книгами.
Обсудив, разработав, найдя способы решения уравнений и систем в своих творческих группах, учащиеся предложат их на обсуждение всему классу.
1. Психологический настрой (рассуждалки «Устами младенца»):
Вопрос: О чем идет речь?
(демонстрируется видеозапись, сделанная учениками начальной школы)
-
Это такая штука, в которой что-то не знаешь, а потом вдруг узнаешь, если захочешь это сделать – и сделаешь.
(Пауза, ответы учащихся)
-
Иногда задачи решаются только с его помощью. Я не люблю их решать, потому что плохо умею это.
(Пауза, ответы учащихся)
-
Не знаю, есть ли у него листья и стебли, но корни у него есть. Может один, а может больше. И только у некоторых нет и корней.
(Пауза, ответы учащихся)
-
Во 2-м классе они – простые, в 7-м – линейные, в 8-м – квадратные, в 10-м – тригонометрические, а в 11-м – иррациональные.
Ответ: Уравнения.
-
Повторение изученных методов решения уравнений.
(Проверка выполнения домашнего задания)
Используются презентация сделанная в PowerPoint
Разбираются и обсуждаются задания разобранные учащимися дома по группам.
(Задания) Решить уравнения
Учащимися составлены презентации к уравнениям, которые сами учащиеся и представляют.
I группа: ![]()
II группа: ![]()
III группа: ![]()
(Перед уроком задания всех групп раздаются каждому ученику)
(От каждой группы один ученик записывает решение первого уравнения своей группы и рассказывает всему классу, учащиеся разбирают и следят за правильностью решения, делая пометки для себя)
№1. Решите уравнение:
![]() .
.
Решение.
Введем обозначения: ![]() тогда 9-x=a3, 7+x=b3.
тогда 9-x=a3, 7+x=b3.
Почленно сложим обе части уравнения: 16=a3+b3.
Имеем систему уравнений:
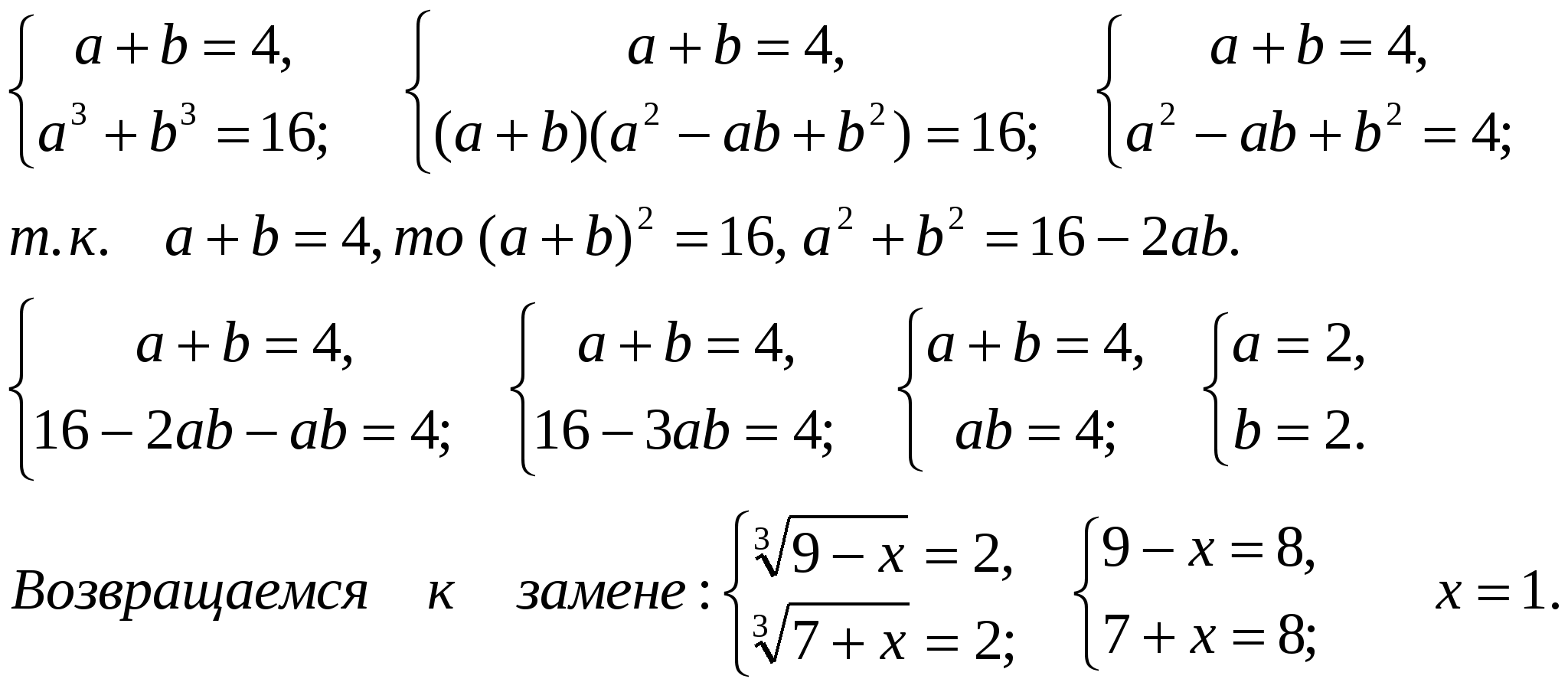
Ответ: х=1.
№2. Решите уравнение: ![]()
![]()
![]()
![]()
Решение.

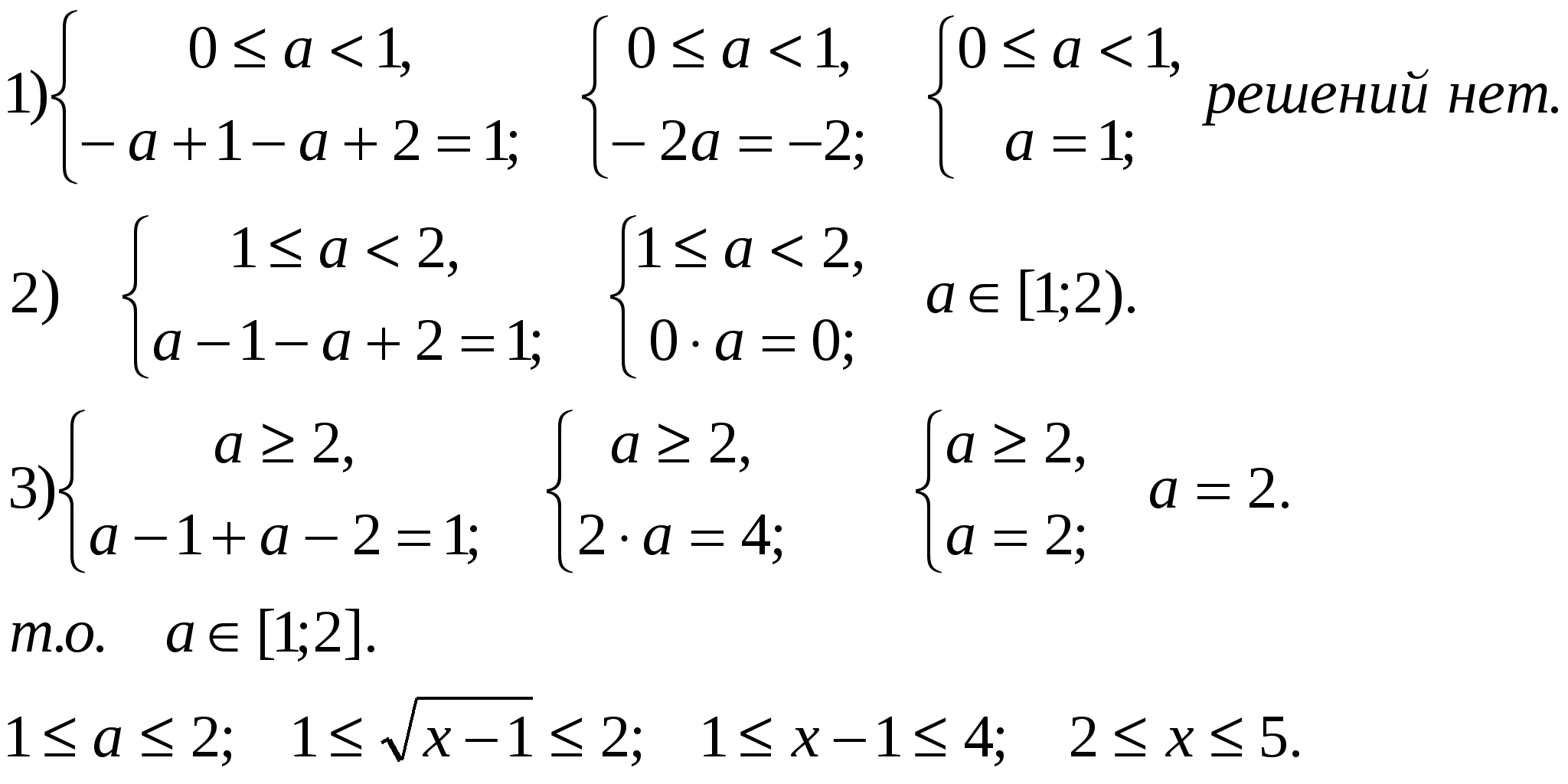
Ответ: [2;5].
№3. Решите уравнение:
![]() .
.
Решение.
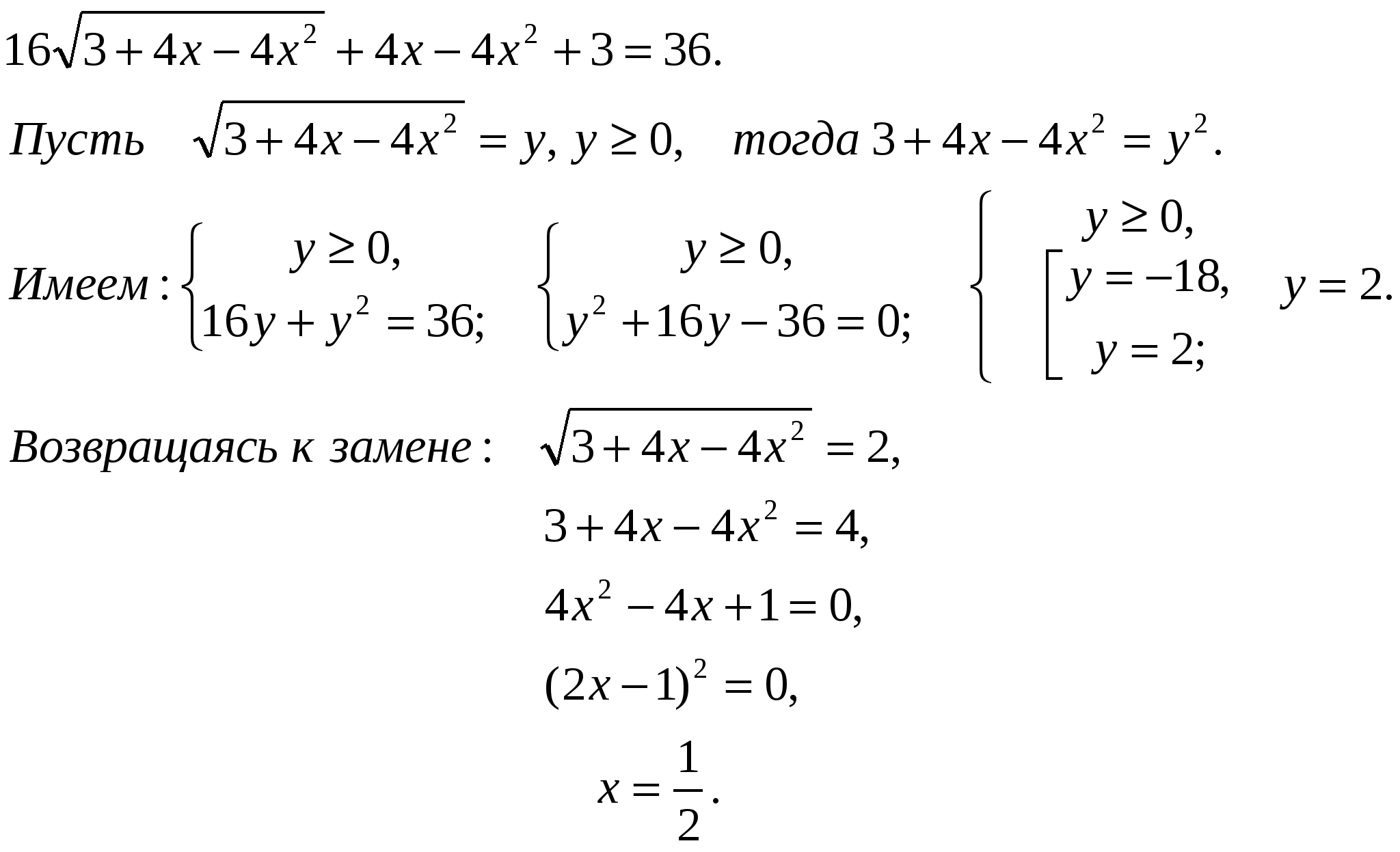
Ответ: ![]() х=0.5
х=0.5
-
Применение новых методов решения уравнений
Учитель:
Мне приходится делить свое время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее потому, что политика существует только для данного момента, а уравнения будут существовать вечно.
А. Эйнштейн
Вы предложили свои решения заданий, а я вам покажу ещё другие методы решения уравнений, которые иногда могут значительно облегчить решение.
1. Использование области определения уравнения.
№4. Решите уравнение:
![]() .
.
Решение.
Выпишем условия, при которых выражения, входящие в левую часть данного уравнения, имеют смысл:
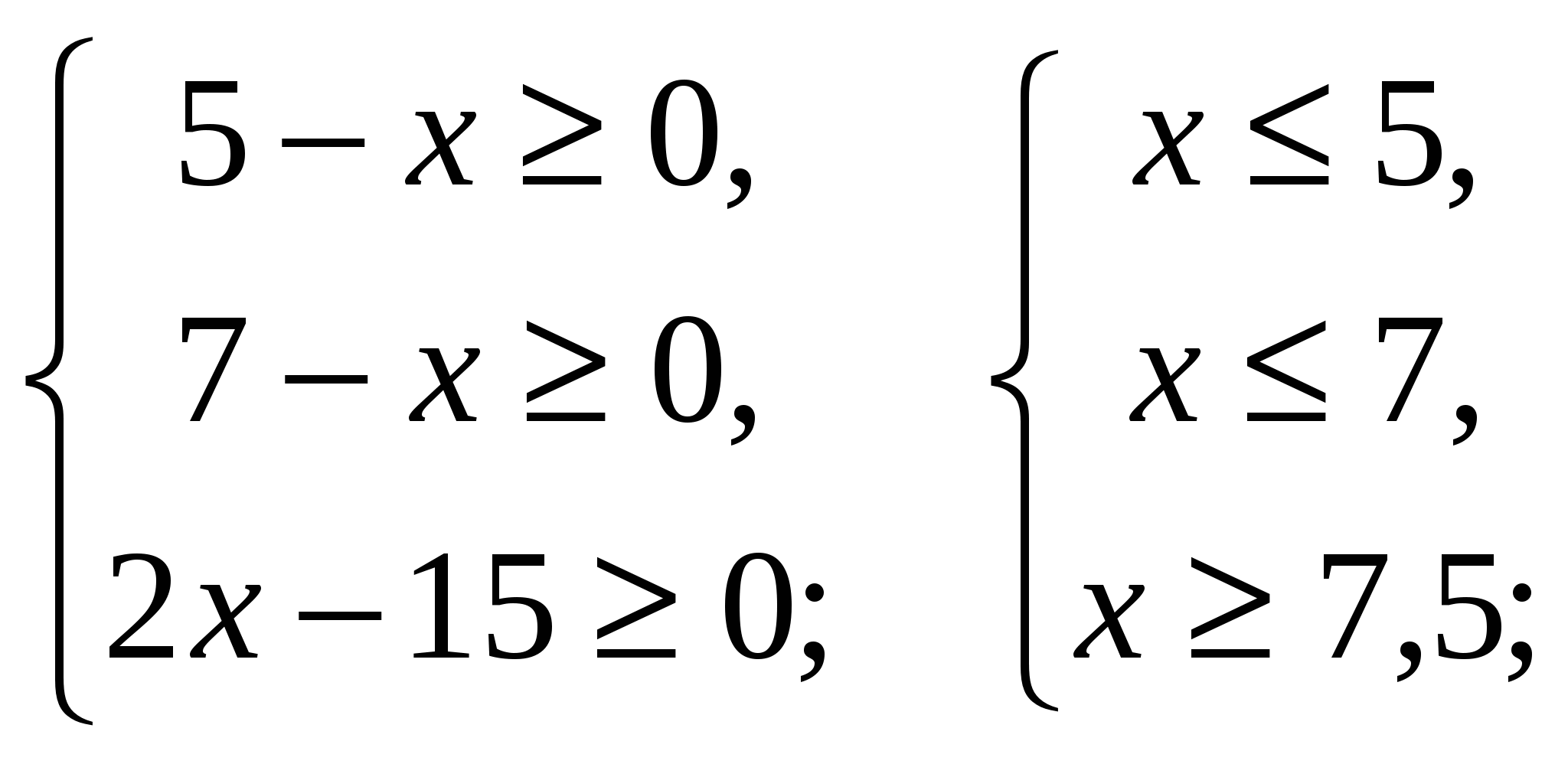
Система решений не имеет. Поэтому и исходное уравнение не имеет решений.
Ответ: решений нет.
Я думаю, Дон, что в моей голове это просто не может уместиться. Я просто не знаю, как мне удастся все это выучить. – Практикой. Немножко теории и много практики, - сказал он. – На это уходит примерно дней десять.
(Р. Бах. Иллюзии.)
Учащимся предлагается для самостоятельного решения три уравнения по группам, затем один из членов группы предлагает решение на доске всему классу
![]()
1 группа (Ответ: 9, -9)
2 группа ![]() (Ответ: корней нет)
(Ответ: корней нет)
![]()
3 группа (Ответ: корней нет)
2. Использование монотонности функции.
Задай еще вопрос. Какое же наслаждение наблюдать за работой собственной головы, решающей мировые проблемы!
(Р.Бах. Иллюзии.)
Повторяется теорема о корне и сопровождается соответствующими слайдами презентации.
Теорема о корне.
Пусть функция f возрастает (или убывает) на промежутке I, число а - любое из значений, принимаемых f на этом промежутке.
Тогда уравнение f(x)=a имеет единственный корень в промежутке I.
Пример: ![]()
Решение.
ОДЗ:![]()
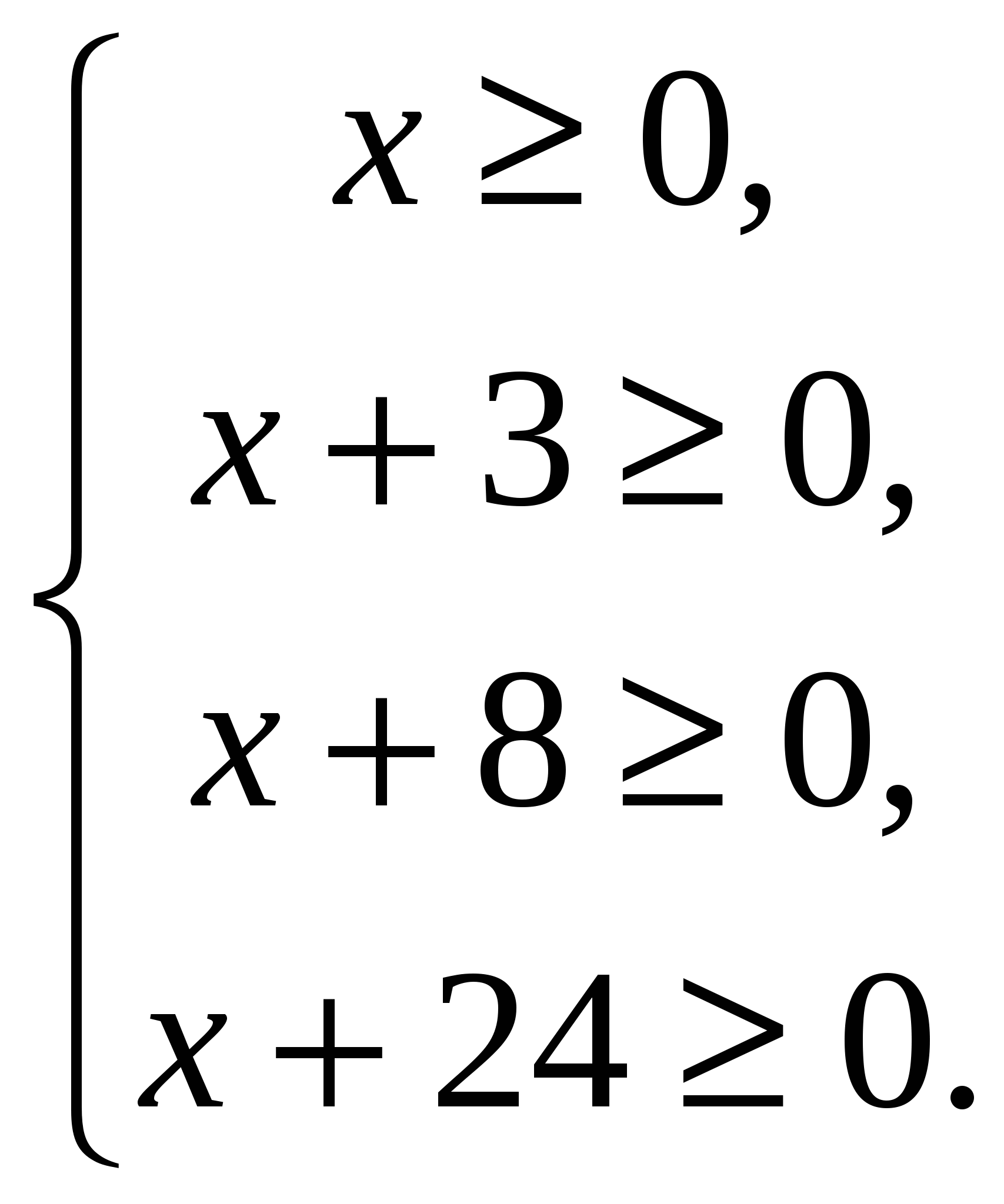
![]() - возрастающая функция (как сумма возрастающих функций).
- возрастающая функция (как сумма возрастающих функций).
Найдем подбором корень, х=1. В силу теоремы о корне, имеем, что он единственный.
Ответ: х=1.
Обобщаем изученные методы решения иррациональных уравнений.
-
Возведение левой и правой частей уравнения в квадрат.
-
Метод подстановки.
-
Применение ОДЗ уравнения.
-
Использование монотонности функции.
IV. Самостоятельная работа учащихся.
Мой дорогой Уотсон, попробуйте немного поанализировать сами, - сказал он с легким раздражением. – Вы знаете мой метод. Примените его, и будет поучительно сравнить результаты.
(А.К. Дойл. Знак четырех.)
Учащимся предлагается решить уравнения предварительно определив метод решения ( возведение в степень, применение ОДЗ уравнения, применение монотонности функций). Задания разбиты на группы.
1 группа: ![]() (Ответ: 9)
(Ответ: 9)
![]() (Ответ: -2)
(Ответ: -2)
![]() (Ответ: -1)
(Ответ: -1)
![]() (Ответ: 8)
(Ответ: 8)
![]() (Ответ: 0,5)
(Ответ: 0,5)
![]() (Ответ: 11)
(Ответ: 11)
![]() (Ответ: 1)
(Ответ: 1)
2 группа: ![]() (Ответ: 8)
(Ответ: 8)
![]() (Ответ: -2)
(Ответ: -2)
![]() (Ответ: 6)
(Ответ: 6)
![]() (Ответ: 2)
(Ответ: 2)
![]() (Ответ: 3)
(Ответ: 3)
![]() (Ответ: 11)
(Ответ: 11)
![]() (Ответ: -1)
(Ответ: -1)
3 группа: ![]() (Ответ: 5)
(Ответ: 5)
![]() (Ответ: 8)
(Ответ: 8)
![]() (Ответ: 0)
(Ответ: 0)
![]() (Ответ: -5)
(Ответ: -5)
![]() (Ответ: нет корней)
(Ответ: нет корней)
![]() (Ответ: 4)
(Ответ: 4)
![]() (Ответ: 7)
(Ответ: 7)
Проверка сам. работы осуществляется нестандартным способом (приложение к интерактивной доске)
При правильном решении работы должна сложиться фраза
«Было трудно, но мы сделали»
-
Домашняя работа.
Решить уравнения.
Решения задач является наиболее характерной и специфической разновидностью свободного мышления.
У. Джеймс
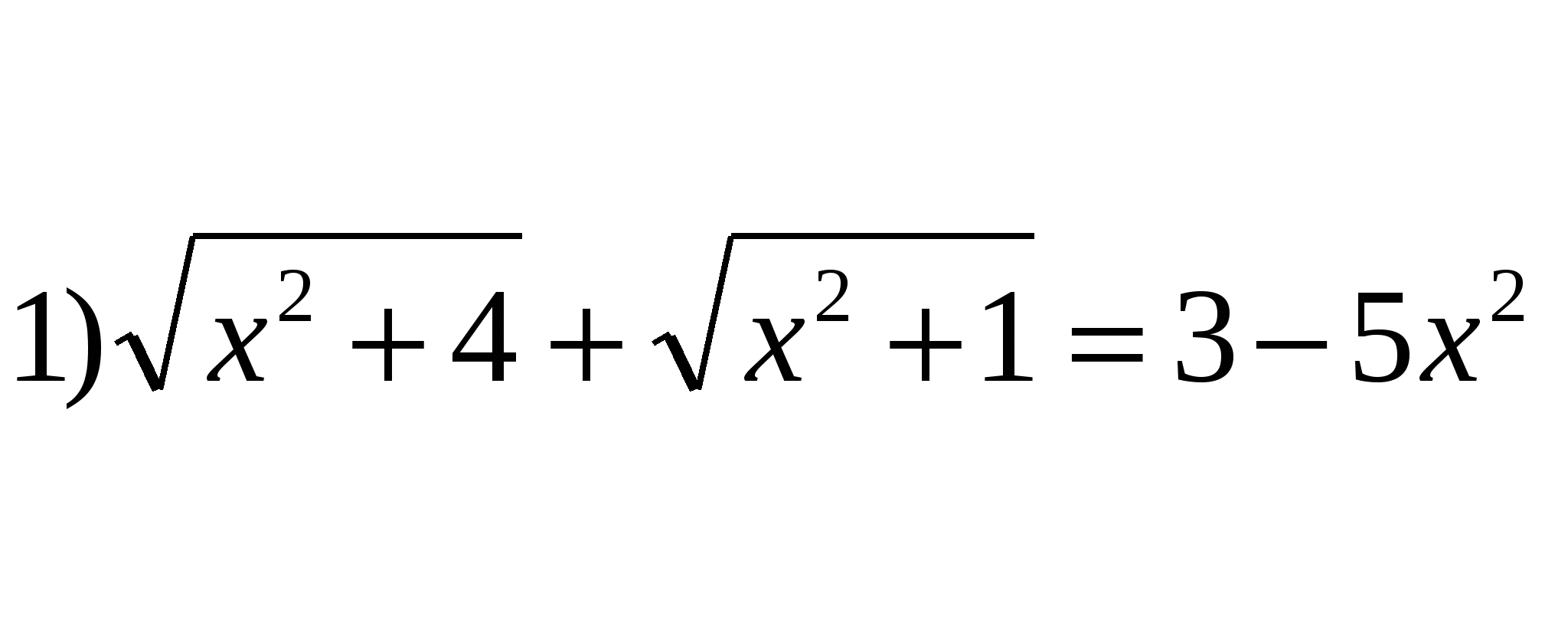
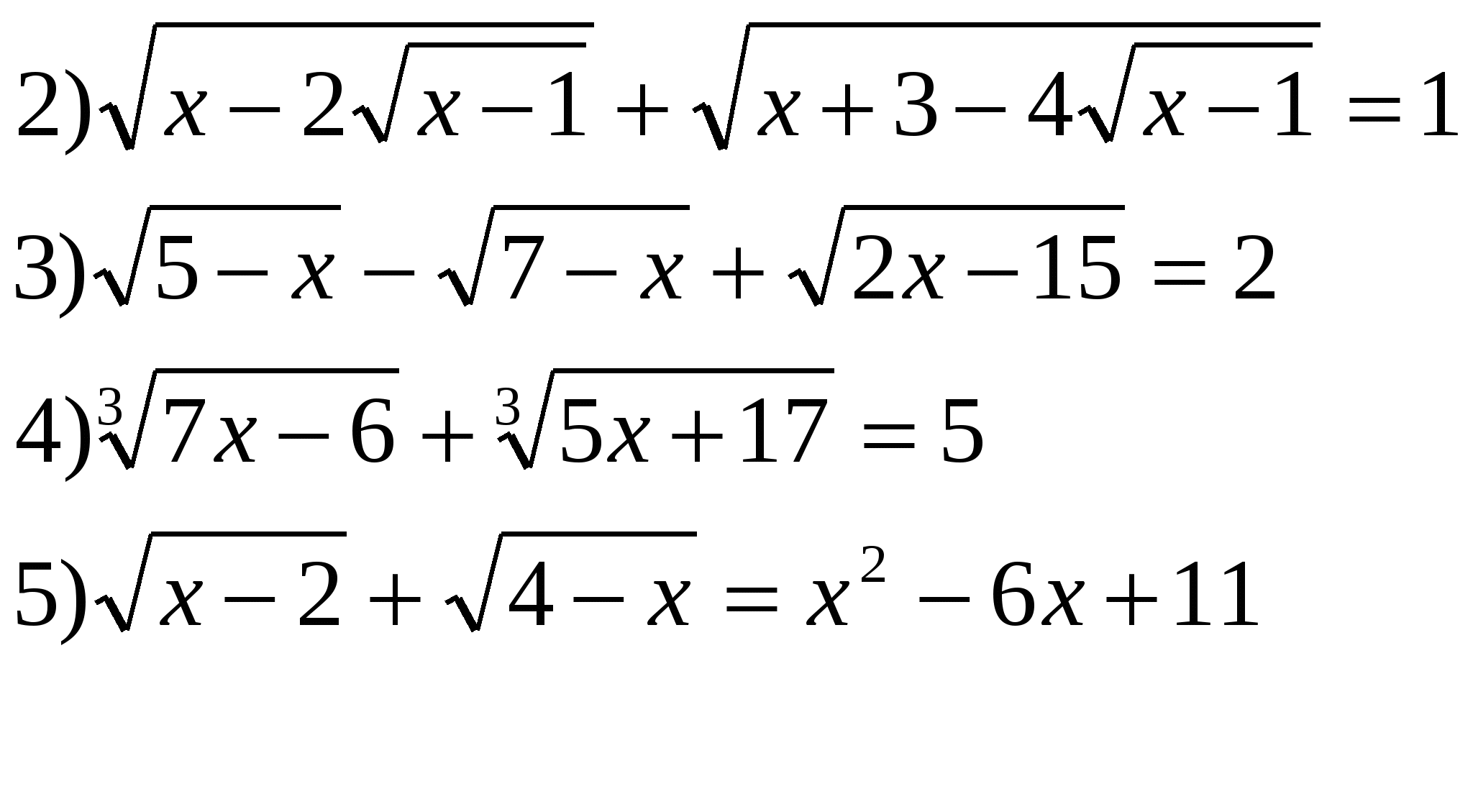
Здесь представлен конспект к уроку на тему «Решение иррациональных уравнений», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (9 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

