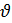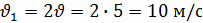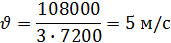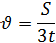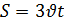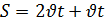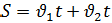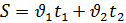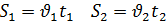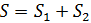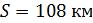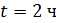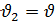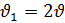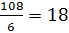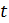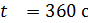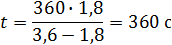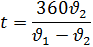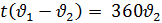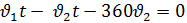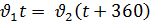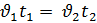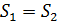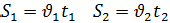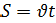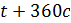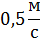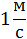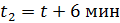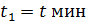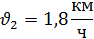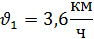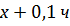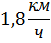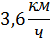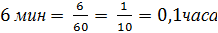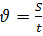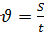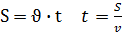Конспект урока «Решение физических задач с помощью линейных уравнений» по алгебре для 6 класса

Выполнила:

Учитель математики СШ №9 г.Петропавловска СКО Республики Казахстан:

Шарипова Айман Сакиновна.

Интегрированный урок математики: «Решение физических задач с помощью линейных уравнений».

Цель: использование математических методов для решения физических задач.

Задачи:

• повторить взаимосвязь таких физических величин как скорость, время, путь, средняя скорость;

• закрепить навык решения физических задач с данными величинами;

• научить решать задачи физического содержания с помощью линейных уравнений;

Методы обучения: проблемный

Формы обучения: Групповая

Оборудование: интерактивная доска, технологические карты.

План урока:

1. Организационный момент.

2. Актуализация имеющихся знаний.

3. Решение задач.

4. Домашнее задание

5. Подведение итогов, рефлексия.

Ход урока:

1. Организационный момент.

- Здравствуйте, дети!

На доске: ФИЗИКА, МАТЕМАТИКА

- На доске записаны два слова. Прочитаем эти слова. Они переплелись неслучайно. Сегодня на уроке мы убедимся, что две науки: математика и физика тесно связаны друг с другом и им друг без друга не обойтись.

2. Актуализация имеющихся знаний.

- У всех на столе есть технологическая карта, которую вы сдадите в конце урока. Подпишем ее, запишем дату сегодняшнего урока, фамилия, имя и класс.

- И для того чтобы приступить к нашему уроку вспомним с вами ранее изученный материал.

Задание 1. Допиши определение.

1. Длина траектории по которой двигалось тело в течение какого-то промежутка времени, называется … (путь)

2. Равенство, в котором неизвестное обозначается буквой, называется … (уравнение)

3. Отношение перемещения к промежутку времени – это … (скорость)

4. Физическая величина, основной единицей которой является секунда – это …(время)

5. Решить уравнение это значит - найти его … (корни или доказать что корней нет)

6. Изменение положения тела или его частей относительно друг друга с течением времени называется механическое … (движение)

7. Уравнение вида ax=b , где x – переменная, a и b – любые числа называется … уравнением с одной переменной. (линейным)

- Заполняем оценочный лист. Все верно – 5 баллов, 2-3 ошибки – 4 балла, 4-5 ошибок – 3 балла, нет верных ответов – 2 баллов.

Задание 2. Найти соответствие. Необходимо соединить стрелочками физическую величину с ее единицей измерения.

Таблица 1. Найди соответствие.

Ответ.

- Заполняем оценочный лист. Все верно – 5 баллов, 2-3 ошибки – 4 балла, 4-5 ошибок – 3 балла, нет верных ответов – 2 баллов.

3. Решение задач.

- Приступим к решению задач. Сегодня мы будем решать с Вами задачи с физической точки зрения и с математической. И в итоге составим алгоритм решения физических задач с помощью линейных уравнений.

-Для этого вспомним формулы для нахождения скорости, времени и расстояния.

Вспомним опорные схемы, которые помогут нам составить уравнение для решения задач.

1 вид. Одна величина + другая величина = сумма величин

2 вид. Одна величина - другая величина = разность величин

3 вид. Одна величина = другая величина

Задача 1.

- Итак, представим себе следующую сказочную ситуацию.

Ученик читает условие задачи:

В лесу мимо пня на котором сидела Маша в 20 часов 00 минут пробежал Медведь со скоростью 1,8 км/ч. Через некоторое время в 20 часов 06 минут Маша пустилась в погоню за Медведем со скоростью 3,6 км/ч. Сколько времени понадобится Маше, чтобы догнать Медведя?

Математический метод.

- Для решения данной задачи нам понадобится.

- Какая физическая величина известна? (скорость)

Чтобы найти взаимосвязь t и S, проследите еще раз за ситуацией. (Учитель показывает на схеме одинаковый (равный) путь, который пробежали Маша и Медведь).

- Какой путь S, пробежал каждый? (одинаковый)

- Что можно сказать о времени t? (время движения Маши на 6 мин больше)

- Как можно выразить 6 мин в часах?

(Учитель на доске)

- Какое время возьмем за х? (наименьшее – время движения Медведя)

- Тогда какое время была в пути Маша? (на 0,1 ч больше, т.е. х+0,1 ч)

- Запишем это в таблицу.

3,6х =1,8(х+0,1)

3,6х –1,8 х – 0,18 = 0

1,8х – 0,18 = 0

1,8х = 0,18

х = 0,18/1,8

х = 0,1 часа – время Маши

Ответ: Время Маши – 0,1 часа.

Физический метод

Дано:

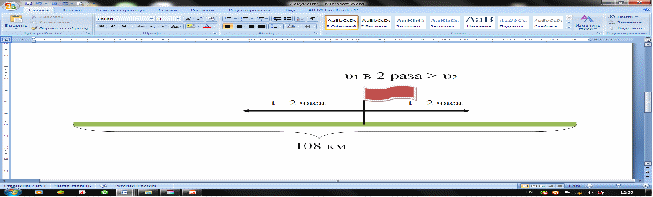
Все верно – 5, 2-3 ошибки – 4, 4-5 ошибок – 3, нет решения – 2.

- Теперь будем решать задачи самостоятельно.

Задача 2. Составьте задачу по рисунку и решите математическим и физическим способом.

Математический метод

Таблица 2

Решение:

υ, км/ч

t, ч

S, км

I

2х

2 ч

4х км

108 км

II

х

2 ч

2х км

Составляем уравнение

4х + 2х = 108

6х = 108

х = км/ч – скорость второго

2х = 2∙18 = 36 км/ч – скорость первого

Ответ: Через 2 часа скорость первого равна 36 км/ч и скорость второго - 18 км/ч.

Физический метод.

Дано:

Все верно – 5, 2-3 ошибки – 4, 4-5 ошибок – 3, нет решения – 2.

4. Домашнее задание

Задача 1. От станции А первый поезд находится на расстоянии 70,5 км, а второй поезд – на расстоянии 56,75 км. Первый поезд едет со скоростью 57 км/ч, а второй – со скоростью 62,5 км/ч. Через сколько часов оба поезда будут на одинаковом расстоянии от станции А.

Задача 2. Составьте по уравнению 7,8х = 9,3(х-10) условие задачи и решите ее.

4. Подведение итогов, рефлексия.

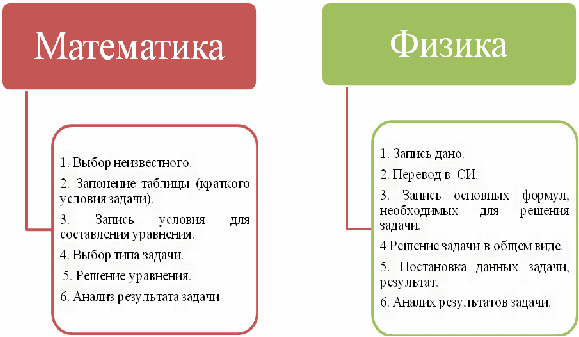
- Итак, сегодня на уроке мы очень плодотворно поработали. Теперь давайте посчитаем свои баллы на оценочном листе и передадим их на первую парту.

Максимальный результат 16 баллов.

20-19 баллов – «5»

18-15 баллов – «4»

14-12 баллов – «3»

11 и менее – «2».

Поднимите руки у кого «5», у кого «4», у кого «3». Молодцы.

Сегодня мы с вами решали физические задачи с помощью уравнения. Давайте сейчас с Вами составим алгоритм решения подобных задач.

Алгоритм решения: