Конспект урока «Целое уравнение и его корни» по алгебре для 9 класса

Интегрированный урок (алгебра + английский язык в 9-м классе)

Тема: "Целое уравнение и его корни"

«The whole equation and its roots»

05.11.2013.

Коваленко Ирина Анатольевна учитель математики

Толстопятова Лидия Евдокимовна, учитель английского языка

Форма урока: Интегрированный урок английского языка и алгебры

Цель:

сформировать представление об алгоритме решения целых уравнений различных типов путём введения одной переменной через интеграцию школьных предметов: алгебры и английского языка.

Задачи: а) образовательная – выявить общие сведения и особенности решения целых уравнений различных типов путём введения новой переменной, закрепить знания учащихся по решению уравнений, способствовать выработке навыков решения уравнений;

• применение знаний, умений, навыков при решении различных типов уравнений;

• развитие навыка самостоятельности в работе.

активизировать употребление в речи Present Simple and Past Simple, Present Perfect в ситуации речевого общения.

б) развивающая - развитие способности обучающихся к распределению внимания, догадке на основе зрительной наглядности и контекста, обобщения фактов и формулирование выводов.

в) воспитательная – формировать коммуникативные умения, способность работать коллективно, повышать мотивацию к изучению новой темы на английском языке.

Оборудование:

интерактивная доска, слайды.

Целесообразность использования медиапродукта – повышение эффективности усвоения материала; развитие исследовательской компетенции обучающихся; интенсификация учебно – воспитательного процесса.

Ход урока.

Мобилизующее начало урока: сообщение темы, цели и хода урока.

Warming up – восприятие и деловой настрой на интегрированный урок. Возбуждение познавательного интереса учителем английского языка.

1. Проверка выполнения домашнего задания:

а) групповая перед уроком самими учащимися;

б) слайд № 1: учитель отвечает на возникшие вопросы при выполнении

домашней работы по своему решению;

Oral work class. Four weak students perform their own examples of optional homework.

в) выборочная ( во время устной работы класса 4 «слабых» ученика выполняют самостоятельно по своему усмотрению одно из заданий из домашней работы на листочках ) – учитель отвечает на вопросы и оценивает работу каждого.

Teacher responds to students' questions and evaluates the work of learners.

English teacher comments on the work of the teacher of mathematics and invites three students to the board for independent work on individual cards.

3. Устная работа ( в это время на доске 3 ученика выполняют самостоятельно работу по карточкам ) – учитель проверяет, отвечает на вопросы и оценивает работу каждого.

You must decide on the instructions of the equation (card number 1)

Карточка № 1:

Решить уравнение: 3х² + 3 _ 2 – 4х - 2 [ Ответ: -2; 1⅓].

You must decide on the instructions of the equation (card number 2)

Карточка № 2:

Решить уравнение: 3х⁴ – 2х² – 1 = 0 [ Ответ: 1; -1].

You must decide on the instructions of the equation (card number 3)

Карточка № 3:

Решить уравнение : ( х² – 4 ) ( х² + 4 ) – (26х² - 41)=0 [Ответ:1; -1; 5; -5]

Let’s turn to a discussion of the slide № 2,3,4,

Слайды № 2, 3, 4.

We are sure that you will cope with the solution of the equations of this type. Suggest to continue our work on the solution of equations of this type

4. Решение целых уравнений различных типов.

Задание № 1.

Решить уравнение ( х² – 7 )² – 4( х² – 7) – 45 = 0.

Problem method of training

Проблемная ситуация.

The teacher puts a problem. The teacher shows a new way of the solution of the equation with one variable

Вопросы учителя: C каким видом уравнения можно сравнить данное? Как к нему прийти? Знаем ли этот способ?

Оформление решения показывает учитель.

Введём новую переменную у = х² -7.

Тогда уравнение примет вид :

у² – 4у – 45 = 0;

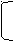у = 9,

у = -5.

Имеем, х² – 7 = 9 или х² – 7 = -5

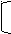
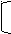х = 4, х = √2,

х = -4. х = -√2.

Ответ: 4; -4; √2; -√2.

Задание № 2.

Решить уравнение:

а) (х² – х + 1) (х² – х – 7 ) = 65 Обсуждается способ решения. Способ найден. Ученики пытаются выполнить задание самостоятельно, при необходимости учитель консультирует индивидуально. По желанию 3 ученика решают на доске. Учитель отвечает на вопросы, проверяет и оценивает работу.

We discussed a way of the solution of the equations with one variable.

We found a new way of the decision.

Will you try to perform a task independently.

Ответ: а) 4; -3 б) 1; -1; 5; -5.

Задание № 3. Самостоятельная работа слабых учеников в паре на листочках. Учитель собирает, проверяет и оценивает работы.

Organization of independent work
of weak pupils. Student self-evaluation.

УМК Ю.Н.Макарычев и др. №276 (а,в).

Ответы ученики проверяют по учебнику. Можно пользоваться шаблоном решения из рабочей тетради.

Задания № 4, 5, 6. Работа с сильными учениками.

Слайд № 5 – ученикам предлагаются 3 уравнения :

- рассматривается первое уравнение;

- способ решения найден;

- желающие продолжают решение на доске;

- группа учеников ищут решение второго уравнения;

- после проверки решения первого уравнения обсуждается способ решения второго и т.д.;

- учитель поощряет учеников оценками за предложенные идеи.

Учитель консультирует, отвечает на вопросы, проверяет и оценивает работу.

Work with strong pupils.

The teacher of Math gives some instructions.

Slide No. 5 – 3 equations are offered to pupils:

- the first equation is considered;

- the way of the decision is found;

- the wishing continue the decision on a board;

- group of pupils look for the solution of the second equation;

- after verification of the solution of the first equation the way of the solution of these equations is discussed

Задание № 4.

Решить уравнение: (х + 1)(х + 3)(х + 5)(х + 7) = 945.

Проблемная ситуация - уравнение другого вида, но почему то рассматривается сейчас, когда применяем метод введения новой переменной.

Учитель рассматривает все предложения учеников. Способ решения – заменить трёхчленами произведение крайних множителей и произведение средних множителей.

Решение: ( х² + 8х + 7 ) ( х² + 8х + 15) = 945.

Введём новую переменную у = х² + 8х.

Тогда уравнение примет вид:

( у + 7) ( у + 15) = 945;

у² + 22 у – 840 = 0;

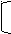у= -42;

у= 20.

Имеем, х² + 8х = -42 или х² + 8х = 20.

нет корней х = -10;

х = 2.

Ответ: -10; 2.

Задание № 5.

Решить уравнение:

(х² +2х)² – (х + 1)² = 55;

Проблемная ситуация: данное уравнение в этой теме, почему? Значит, можно решить путём введения новой переменной. Как преобразовать левую часть уравнения? Способ решения найден – ( х + 1)² = х² + 2х + 1.

Ответ: -4; 2.

Задание № 6.

Решить уравнение : х² – 4 + х - 3⅓

х х² -4-

Проблемная ситуация: данное уравнение в этой теме, почему?

Способ решения найден. Вводим новую переменную У = х² – 4

х

Уравнение примет вид: у + 1 = 3⅓

у

Ответ: 4; -1; 1 + √145; 1 - √145

6 6

5. Домашнее задание :

Обязательный уровень: УМК Ю.Н. Макарычев и др. № 276(б,г), №282(а);

Творческий уровень: №274 (а), №370(а).

6. Итог урока:

- оценку за работу на уроке получил каждый ученик ;

- учитель доволен объёмом выполненной работы.

Lesson result:

- the assessment for work at a lesson was received by each pupil;

- the teacher is happy with the volume of the performed work.

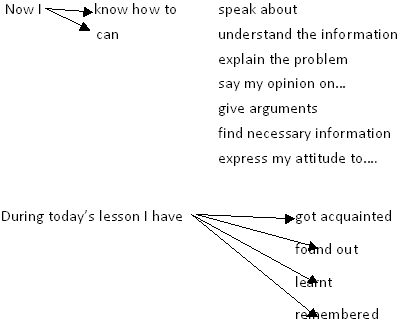
7. Рефлексия. Reflection.

Каждый ученик формулирует итоги урока, используя схему, где он соединяет и обобщает свои впечатления, используя в речевом высказывании грамматические структуры в Present Simple, Past Simple, Present Perfect.