Конспект урока «Решение квадратных уравнений. Теорема Виета. Разложение квадратного трёхчлена на множители» по алгебре для 8 класса
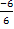
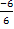
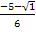
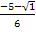









 Для учителя Урок алгебры в 8 классе
Для учителя Урок алгебры в 8 классе
Тема: «Решение квадратных уравнений. Теорема Виета. Разложение квадратного трёхчлена на множители»
Цель: совершенствовать навыки решения квадратных уравнений по формуле корней, совершенствовать навык применения теоремы Виета; научиться раскладывать квадратный трёхчлен на множители и выполнить проверочную работу.
Вид урока: комбинированный
Оборудование: компьютер, проектор, слайды, учебник Алгебра – 8 под ред. А.Абылкасымова, тетрадь.
Ход урока:
.0. Проверяем домашнее задание ____________________
1. Теория «Ищи слабое звено» ( 1 вопрос – 1 балл)
1)определение квадратного уравнения (взаимопроверка)
2)Теорема Виета (взаимопроверка)
3)Теорема обратная теореме Виета (взаимопроверка)
4) Ответь на эти вопросы учителю.
2.Заполни таблицу 1, решив предварительно уравнения в рабочей тетради.
Проверь ответы по ключу на доске (слайд 2).
Таблица 1.
| Уравнение | Дискриминант | Х1 | Х2 | |
| 1. | Х2 - 4х +3 =0 | 4 | 1 | 3 |
| 2. | Х2+х -2 =0 | 9 | -2 | 1 |
| 3. | 2х2 +3х +1=0 | 1 | -0,5 | -1 |
| 4. | 3х2 + 7х -6 =0 | 121 | -3 | 2/3 |
| 5. | 11х – 4х2+3=0 | 169 | -0,25 | 3 |
Оценка: 1 уравнение – 1 балл
3. Заполните таблицу 2 , применив теорему Виета. Обсуди с товарищем (взаимопроверка)
Проверка ( слайд 3)
| Уравнение | х1+х2 | Х1∙х2 | Корни х1 и х2 | |
| 1. | Х2-5х + 6 =0 | 5 | 6 | 2 и 3 |
| 2. | Х2 +7х +12 =0 | -7 | 12 | -3 и -4 |
| 3. | Х2 - 4х -5 =0 | 4 | -5 | -1 и 5 |
| 4. | 2х2+18х+40 =0 | -9 | 20 | -4 и -5 |
| 5. | 9х-х2-8 =0 | 9 | 8 | 1 и 8 |
Оценка: 1 уравнение – 1 балл
4. «Ищи ошибку» (слайд 4) « Кто ничего не замечает,
Тот ничего не изучает.
Кто ничего не изучает
Тот вечно хнычет и скучает».
Ученик 8 класса решил два уравнения. Проверь решение и исправь ошибки.
1)х2 – х - 12 = 0 2) - 3х2 + 5х +2 =0
Решение: D = b2 – 4 ac Решение: 3х2 - 5х -2 =0
D = -12 - 4∙1∙(- 12) = - 49 нет корней D = b2 – 4 ac
D = (-5)2-4∙3∙(- 2) = 25 – 24= 1 два корня
Х1= х2 =
Х1 = = = -
1 уравнение- 1 балл х2 = = = 1
Реши ( взаимопроверка ). Проверь по ключу ( слайд 5)
6. Выучи правило разложения квадратного трёхчлена на множители:
Разложить квадратный трёхчлен ах2 + bx + c на множители значит представить его в виде
a( x – x1)∙(x – x2), где а – первый коэффициент, х1 и х2 – корни квадратного трёхчлена.
Запомни ах2 + bx +c = a(x – x1)∙(x – x2)
Если D= 0, то квадратный трёхчлен имеет два равных корня и разложение на множители имеет вид
ax2 +bx +c = a(x – x1)2
Если квадратный трёхчлен не имеет корней, то разложить такой трёхчлен на множители нельзя.
7. Вопросы учителя:
-
Что надо знать, чтобы разложить квадратный трёхчлен на множители?
-
Как разложить квадратный трёхчлен на множители ? (формула)
-
Можно ли разложить квадратный трёхчлен на множители, если он не имеет корней?
-
Как раскладывается квадратный трёхчлен на множители, если он имеет один корень?
8. Разложи на множители квадратные трёхчлены ( взаимопроверка)
Проверка ( слайд 6)
-
Х2-4х +3 ; 2) 3х2 + 5х -2 ; 3)4х2 -12х + 9
9. Самостоятельная работа ( оценивается отдельно)
| 2 вариант | |
| Решите уравнение : а)2х2 -5х +10 =0 б)6х2 + 7х + 1 =0 | Решите уравнение : а) 3х2 +7х+2 =0 б)2х2-3х+5=0 |
| Найди корни, используя т.Виета: х2- 11х +24 =0 | Найди корни, используя т.Виета: х2-9х + 8 =0 |
| Разложите на множители: а) х2+3х -18 б)2х2 +3х + 1 | Разложите на множители: а) х2 – 7х + 6 б)5х2 -7х +2 |
( Работы проверяются после сдачи тетрадей)
10. Учитель:
1)какова была цель нашего урока?
2)Как вы считаете, цель урока достигнута?
3) Итак, если цель достигнута, то блиц-вопрос:
Разложите квадратный трёхчлен на множители: х2 - 7х +6 ( 1 балл)
11.Истользуя критерий оценивания, оцените свою работу, занесите оценку в оценочный лист.
12.Итоги урока и домашнее задание:
Для ученика Блок - предписание
Тема: «Решение квадратных уравнений. Теорема Виета. Разложение квадратного трёхчлена на множители».
Цель: совершенствовать навыки решения квадратных уравнений по формуле корней, совершенствовать навык применения теоремы Виета; научиться раскладывать квадратный трёхчлен на множители и выполнить проверочную работу
1. Теория «Ищи слабое звено»
Ответь на вопросы товарищу( поставь оценку в оценочный лист, 1 вопрос – 1балл)
1)определение квадратного уравнения (взаимопроверка)
2)Теорема Виета (взаимопроверка)
3)Теорема обратная теореме Виета (взаимопроверка)
4) Ответь на эти вопросы учителю.
2.Заполни таблицу 1, решив предварительно уравнения в рабочей тетради.
Проверь ответы по ключу на доске (слайд 2).
Таблица 1.
| Уравнение | Дискриминант | Х1 | Х2 | |
| 1. | Х2 - 4х +3 =0 | | | |
| 2. | Х2+х -2 =0 | | | |
| 3. | 2х2 +3х +1=0 | | | |
| 4. | 3х2 + 7х -6 =0 | | | |
| 5. | 11х – 4х2+3=0 | | | |
Оценка: 1 уравнение – 1балл
3. Заполните таблицу 2 , применив теорему Виета. Обсуди с товарищем (взаимопроверка)
Проверка ( слайд 3)
| Уравнение | х1+х2 | Х1∙х2 | Корни х1 и х2 | |
| 1. | Х2-5х + 6 =0 | | | |
| 2. | Х2 +7х +12 =0 | | | |
| 3. | Х2 - 4х -5 =0 | | | |
| 4. | 2х2+18х+40 =0 | | | |
| 5. | 9х-х2-8 =0 | | | |
Оценка: 1 уравнение – 1 балл
4. «Ищи ошибку» ( слайд 4) Кто ничего не замечает
Тот ничего не изучает.
Кто ничего не изучает
Тот вечно хнычет и скучает.
Ученик 8 класса решил два уравнения. Проверь решение и исправь ошибки.
1)х2 – х - 12 = 0 2) - 3х2 + 5х +2 =0
Решение: D = b2 – 4 ac Решение: 3х2 - 5х -2 =0
D = -12 - 4∙1∙(- 12) = - 49 нет корней D = b2 – 4 ac
D = (-5)2-4∙3∙(- 2) = 25 – 24= 1 два корня
Х1=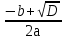 х2 =
х2 = 
Х1 = =
=  = -
= - 
х2 =  =
=  = 1
= 1
Оценка: 1 уравнение – 1 балл
5. Реши № ( взаимопроверка ). Проверь по ключу ( слайд 8)
6. ( слайд 9)
Выучи правило разложения квадратного трёхчлена на множители:
Разложить квадратный трёхчлен ах2 + bx + c на множители значит представить его в виде
a( x – x1)∙(x – x2), где а – первый коэффициент, х1 и х2 – корни квадратного трёхчлена.
Запомни ах2 + bx +c = a(x – x1)∙(x – x2)
Если D= 0, то квадратный трёхчлен имеет два равных корня и разложение на множители имеет вид
ax2 +bx +c = a(x – x1)2
Если квадратный трёхчлен не имеет корней, то разложить такой трёхчлен на множители нельзя.
7. (слайд 10)
Ответь товарищу на вопросы учителя:
1) Что надо знать, чтобы разложить квадратный трёхчлен на множители?
2)Как разложить квадратный трёхчлен на множители ? (формула)
3)Можно ли разложить квадратный трёхчлен на множители, если он не имеет корней?
4)Как раскладывается квадратный трёхчлен на множители, если он имеет один корень?
( Оцени ответ товарища 1 вопрос – 1 балл 8.( слайд 11) Разложи на множители квадратные трёхчлены ( взаимопроверка)
Проверка ( слайд 11)
-
Х2-4х +3 ; 2) 3х2 + 5х -2 ; 3)4х2 -12х + 9
Оценка: 1 пример – 1 балл
9. слайд 12 Самостоятельная работа ( оценивается отдельно)
Проверь по ключу (слайд 13) – поставь оценку в оценочный лист.
| 2 вариант | |
| Решите уравнение : а)2х2 -5х +10 =0 б)6х2 + 7х + 1 =0 | Решите уравнение : а) 3х2 +7х+2 =0 б)2х2-3х+5=0 |
| Найди корни, используя т.Виета: х2- 11х +24 =0 | Найди корни, используя т.Виета: х2-9х + 8 =0 |
| Разложите на множители: а) х2+3х -18 б)2х2 +3х + 1 | Разложите на множители: а) х2 – 7х + 6 б)5х2 -7х +2 |
( работы проверяются после сдачи тетрадей)
10. Ответь товарищу на вопросы учителя:
1)какова была цель нашего урока?
2)Как вы считаете, цель урока достигнута?
3) Итак, если цель достигнута, то блиц-вопрос:
Разложите квадратный трёхчлен на множители: х2 - 7х +6 ( 1 балл)
-11. Подсчитайте общее число баллов. Используя критерий оценивания, оцените свою работу
и поставьте оценку в оценочный лист.
12. Итоги урока и домашнее задание:
Блок - предписания и индивидуальные оценочные листы раздаются обучающимся, которые работают по ним самостоятельно, решая задания, выполняют взаимопроверку и ставят баллы в оценочный лист; задания можно проверить по слайдам сразу после их выполнения и также проставить баллы в оценочный лист.
Оценочный лист
Фамилия, имя______________________________________________________
Тема: « Решение квадратных уравнений. Теорема Виета. Разложение квадратного трёхчлена на множители"
| Задание | Оценка | |||
| 1 | « Ищи слабое звено». Проверка теории. | | ||
| 2 | Таблица 1 | | ||
| 3 | Таблица 2 | | ||
| 4 | « Ищи ошибку» | | ||
| 5 | № из учебника | | ||
| 6 | Ответы на вопросы по разложению трёхчлена на множители | | ||
| 7 | Разложить на множители квадратные трёхчлены | | ||
| 8. | Дополнительные ответы | | ||
| | Общий балл | | ||
| | Оценка за урок | | ||
| 9. | Самостоятельная работа (Вариант №_______ ) | | ||
Критерий выставления оценки за урок:
-
22-29 баллов – «5»(отлично);
-
17-21 балл – «4»( хорошо);
-
13- 16 баллов – «3»(удовлетворительно);
-
Если меньше 13 баллов : начните изучение этой темы сначала, у вас - «2» (неудовлетворительно).
__________________________________________________________________________________________
Блок - предписания и индивидуальные оценочные листы раздаются обучающимся, которые работают по ним самостоятельно, решая задания, выполняют взаимопроверку и ставят баллы в оценочный лист; задания можно проверить по слайдам сразу после их выполнения и также проставить баллы в оценочный лист.
Оценочный лист
Фамилия, имя______________________________________________________
Тема: « Решение квадратных уравнений. Теорема Виета. Разложение квадратного трёхчлена на множители"
| Задание | Оценка | |||
| 1 | « Ищи слабое звено». Проверка теории. | | ||
| 2 | Таблица 1 | | ||
| 3 | Таблица 2 | | ||
| 4 | « Ищи ошибку» | | ||
| 5 | № из учебника | | ||
| 6 | Ответы на вопросы по разложению трёхчлена на множители | | ||
| 7 | Разложить на множители квадратные трёхчлены | | ||
| 8. | Дополнительные ответы | | ||
| | Общий балл | | ||
| | Оценка за урок | | ||
| 9. | Самостоятельная работа (Вариант №_______ ) | | ||
Критерий выставления оценки за урок:
-
22-29 баллов – «5»(отлично);
-
17-21 балл – «4»( хорошо);
-
13- 16 баллов – «3»(удовлетворительно);
-
Если меньше 13 баллов : начните изучение этой темы сначала, у вас - «2» (неудовлетворительно).
Здесь представлен конспект к уроку на тему «Решение квадратных уравнений. Теорема Виета. Разложение квадратного трёхчлена на множители», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (8 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

