Конспект урока «Решение однородных тригонометрических уравнений» по алгебре для 10 класса

Деятельность обучающихся

Познавательная

Коммуникативная

Регулятивная

Осуществляемые действия

Формируемые способы деятельности

Осуществляемые действия

Формируемые способы деятельности

Осуществляемые действия

Формируемые способы деятельности

1

2

3

4

5

6

7

Первый этап : актуализация имеющихся знаний (8 мин.)

1. Учитель создает ситуацию успеха для формирования и повышения учебной мотивации,

Дает задания, которые ученики выполняют известным способом (актуализация знаний),

организует фронтальную работу по проверке знаний.

Решают задания

1.Устно:

sin x=-1;cos x=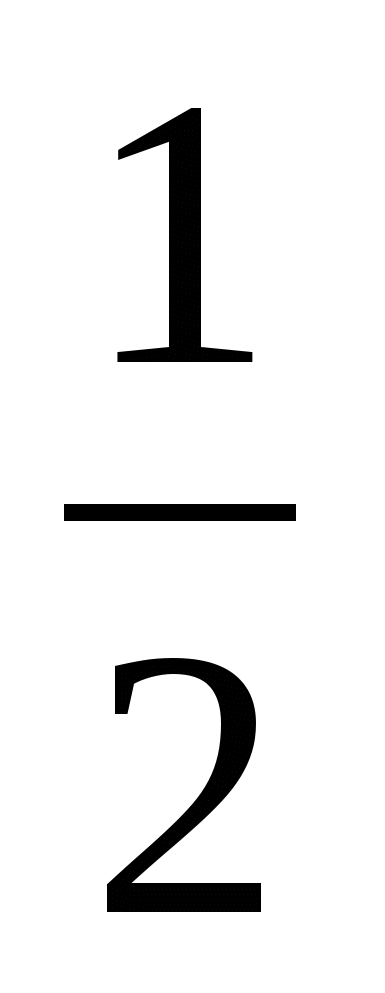 ;tg x=-1;

sin (π+x)=0

tg x=4; sin x=-2;

2. Письменно (по вариантам)

1) 2sinx cos 5x – cos 5x =0;

2)3cos²x – sinx – 1 =0

У доски два ученика демонстрируют и проговаривают ход своего решения задания №2

Актуализация знаний

взаимодействуют с учителем во время опроса, осуществляемого во фронтальном режиме.

контролируют правильность ответов обучающихся

остальные учащиеся

сопоставляют своё решение с решением на доске и выполняют самопроверку

Осуществляют

взаимоконтроль

Второй этап: фиксация затруднения в деятельности (10 мин)

1.Учитель проецирует на экране задание

2.Организует показ работ нескольких учеников через документ-камеру.

3. Учитель задает вопрос :

В чем затруднение?

Уточняет причину затруднения при выполнении задания

3. Организует поисковую работу в группах,

предлагает ученикам обсудить пути решения данной проблемы.

1.Самостоятельно решают предложенные задания.

1)3tg²x + 2tgx -1=0

2) 2 cos2 x + 9cos x +14=0;

3)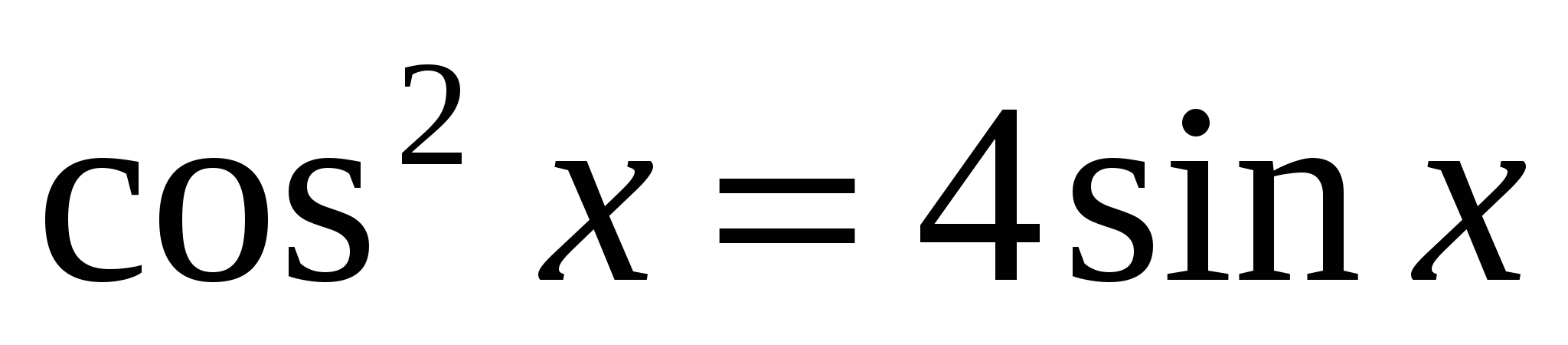

.4)

5)2sinx – 3cosx = 0

6) 3sin²x – 4sinx cosx + cos²x = 0

Ученики указывают на затруднение в случае

5) и 6)

уточняют, в чём затруднение, почему не срабатывает известные методы

Самостоятельная работа в группах над проблемой.

самостоятельное выделение-формулирование познавательной цели, постановка и формулирование проблемы, решение проблемы.

вступают в диалог, с достаточной точностью выражают свои мысли

инициативное сотрудничествос учителем и сверстниками. .

анализируют ситуацию, фиксируют затруднение .

контроль, коррекция, выделение и осознание того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения;

волевая саморегуляция в ситуации затруднения.

Проектирование способа деятельности (8мин)

1. Организовывает работу обучающихся над формулированием гипотез и их обоснованием.

2.Слушает все ответы, задаёт вопросы:

1.Чем отличаются данные уравнения?

2.Как составлены данные уравнения?

3.Какое название дали бы данным уравнениям?

4.Почему возможно деление на sinx или на cosx?

3. Учитель предлагает сравнить определение, название, метод решения, которые они получили, с определением, названием, методом решения авторов учебника. Создает ситуацию успеха.

2sinx – 3cosx = 0/: cosx ≠ 0

2sinx — 3cosx = 0

cosx cosx cosx

2tgx – 3 = 0

2tgx = 3

tgx = 1,5

Ответ: x = arctg1,5 + πn, n € Z

б) 3sin2x – 4sinxcosx + cos2x = 0

Каждая группа предлагает свое решение, фиксирует его на доске.

Дают определение новому виду уравнений, сравнивают с другими видами уравнений, дают название данным уравнениям, проговаривают этапы решения уравнений данного вида.

Сравнивают свое определение, название, метод решения с авторами учебника, делают выводы.

asinx + bcosx = 0, a,b ≠ 0 и

asin²x + bsinxcosx+ kcos²x = 0, a,b,k ≠ 0 –однородные уравнения 1 и 2 степени.

выдвижение гипотез и их обоснований, построение логической цепи рассуждений

вступают в диалог с обучающимися других групп и учителем, с достаточной точностью выражают свои мысли

анализируют предложенные идеи и версии, находят новый, метод решения однородных тригонометрических уравнений.

умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации

Прогнозирование результата, умение высказывать свое предположение, составлять план деятельности

1.Организует работу обучающихся над усвоением нового способа. На доске записаны уравнения.

Найти среди уравнений однородные, определить их вид и решить.

1.sinx = 2cosx

2. √3sin3x – cos3x = 0 –

3. sin2x – 2sinx – 3 = 0 –

4. 2cos2x + 3sin2x + 2cosx = 0

5.6sin2x – cos2x –5sinxcosx = 0

Учащиеся должны назвать вид уравнения и объяснить, как его можно решить.

2.Анализирует ошибки, выясняет причины возникновения ошибок.

Решают задания новым методом (один обучающийся выполняет у доски, проговаривая своё решение.)

Задание один ученик решает на обратной стороне доски, остальные обучающиеся решают самостоятельно.

Проверка решений, анализ ошибок.

Затем обучающиеся самостоятельно решают задания. С помощью интерактивной доски они выполняют самопроверку и выставляют отметки на полях карандашом, руководствуясь критериями оценивания.

Оценивание, осуществление итогового и пошагового контроля по результату.

Учитель предлагает выполнение заданий с целью проверки усвоения знаний.

Рефлексия:

• Что нового узнали на уроке?

• Чему научились?

• В чём испытывали трудности?

• Оцените свою работу на уроке.

Обучающиеся решают задания по вариантам самостоятельно.

Выполняют взаимопроверку, ставят по одному баллу за каждый правильный ответ(ответы на доске).

Выставляют оценки в тетрадь.

Обучающиеся дают ответы на поставленные вопросы.

(10мин)

осознание уровня и качества усвоения; контроль

Домашнее задание (4мин)

(цель: дать установку на отработку определенных умений)

Учитель предлагает дифференцированное домашнее задание.

Выставляет обучающимся отметки за работу на уроке в журнал.

Обучающиеся должны сами сделать выбор, какое задание выполнить, получая его на листочках у учителя.