Конспект урока «Решение тригонометрических уравнений» по алгебре для 10 класса
Муниципальное бюджетное общеобразовательное учреждение
МО г. Нягань
«Средняя общеобразовательная школа №6»
РАЗРАБОТКА УРОКА ПО АЛГЕБРЕ И НАЧАЛАМ АНАЛИЗА
В 10 классе
«Решение тригонометрических уравнений»
Составила:
Запонюк Инна Мухтаровна,
учитель математики высшей квалификационной категории
г.Нягань
Решение тригонометрических уравнений.
Цель: отработать навыки решения простейших тригонометрических уравнений;
выработать у учащихся навыки решения более сложных тригонометрических
уравнений, выделив общую идею решения: приведение уравнений к виду,
содержащему лишь одну тригонометрическую функцию одного аргумента
с последующей заменой переменной, или разложения на множители.
Ход урока.
-
Организационный момент.
-
Повторение. Актуализация опорных знаний.
Повторить общие формулы решения простейших тригонометрических уравнений : 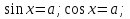 tg х = а, где а – действительное число.
tg х = а, где а – действительное число.
Вспомнить условие, при котором уравнения 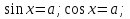 не имеют решения.
не имеют решения.
Повторить формулы для частных случаев , когда а = 1, -1, 0.
Повторить формулы для решения квадратного уравнения.
-
Устный счёт (слайд № 3, 4)
Вычислить.
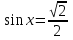
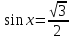
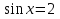
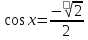
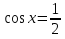
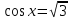
tg х = 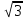 tg х =
tg х =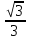 tg х = 5
tg х = 5
sin x = 1 sin x = -1 sin x = 0
cos x = 1 cos x = -1 cos x = 0
tg x = 1 tg x = -1 tg x = 0
-
Изучение нового материала.
Учитель: Если в уравнение входят разные тригонометрические функции, то их, если возможно, надо выразить через одну. При этом нужно выбрать эту функцию так, чтобы получилось квадратное уравнение относительно её. Введя новую переменную и решив квадратное уравнение, перейти к решению одного из простейших тригонометрических уравнений.
А) (слайд № 5)
Уравнения, приводимые к квадратным: 2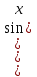
Это квадратное уравнение относительно 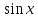 . Введем переменную у=
. Введем переменную у=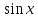 . Тогда уравнение примет вид:
. Тогда уравнение примет вид:
2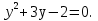 Здесь:
Здесь: 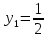 ,
, 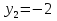 .
.
-
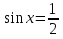 , х=
, х=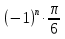 +
+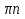 , n
, n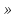 Z.
Z. -
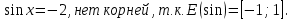
Ответ: х=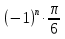 +
+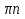 , n
, n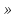 Z.
Z.
Б) (слайд № 6)
Уравнения, приводимые к квадратным: 6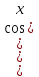
Заменяя 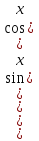 , получим:
, получим:
6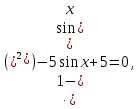
6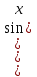 +5
+5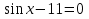 .
.
Пусть у=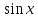 , тогда 6
, тогда 6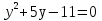 ,
, 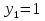 ,
, 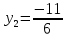 .
.
-
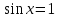 ,
, 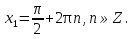
-
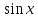 =-
=-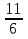 , корней нет, т.к.
, корней нет, т.к. 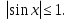
Ответ: х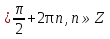
В) (слайд № 7)
Уравнения, приводимые к квадратным: tgx+3ctgx = 4
Заменяя ctgx=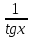 , получим tgx+
, получим tgx+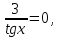
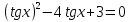 , ОДЗ: x
, ОДЗ: x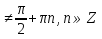 .
.
Квадратное уравнение относительно tgx, пусть tgx=у, тогда 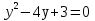 ,
, 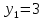 ,
, 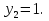
-
tgx=3,
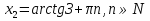
-
tgx=1,
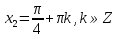
Г) (слайд № 8)
Вынесение общего множителя: 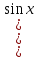 -
- 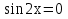
Заменяя sin2x=2sinx cosx, получим
cosx, получим 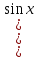 - 2sinx
- 2sinx cosx=0. Разложим левую часть на множители: sinx(sinx- 2cosx)=0.
cosx=0. Разложим левую часть на множители: sinx(sinx- 2cosx)=0.
-
sinx=0, x=
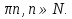
-
sinx - 2cosx = 0 – однородное уравнение 1 степени. Делим обе части на cosx
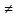 0 (иначе и sinx =0, что невозможно, т. к.
0 (иначе и sinx =0, что невозможно, т. к. 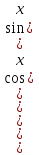 ),получим tgx=2,x=arctg2+
),получим tgx=2,x=arctg2+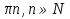
Ответ: x=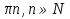 ; x=arctg2+
; x=arctg2+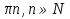
Д) (слайд № 9)
Однородные уравнения II степени: 22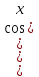
Представим 7=7 1=7
1=7 (
(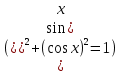 , получим однородное квадратное уравнение II степени. Разделим обе части на
, получим однородное квадратное уравнение II степени. Разделим обе части на 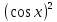 ,
, 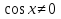 (иначе и
(иначе и 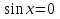 , что невозможно, т.к. (
, что невозможно, т.к. (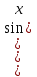 =1), получим 7
=1), получим 7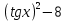 tgx- 15=0. Пусть tgx=у , 7
tgx- 15=0. Пусть tgx=у , 7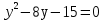 ,
, 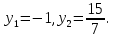
Е) (слайд № 10-11)
Однородные уравнения II степени: 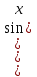 -5
-5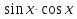 +6(
+6(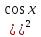 =0
=0
В них каждое слагаемое II степени. Решаются делением обеих частей на 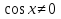 (или
(или 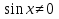 ).
).
Разделим обе части на (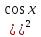 ,
, 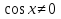 (иначе
(иначе 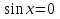 , что невозможно, т.к.
, что невозможно, т.к. 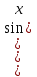 ), получим
), получим 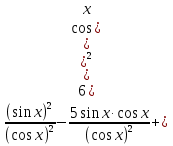 ,
,
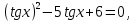
tgx = y, 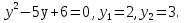
-
tgx=2, x=arctg2+
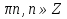
-
tgx=3, x=arctg3+
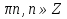
Ответ: x=arctg2+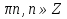 ; x=arctg3+
; x=arctg3+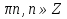 .
.
-
Работа с учебником (слайд № 12) № № 18.6 – 18.12 (а)
-
Домашнее задание по вариантам. (Слайд №13)
-
Итог урока
-
С какими типами уравнений мы сегодня познакомились?
-
Какими известными вам способами их можно решить?
Методические рекомендации для учителей.
ИКТ сопровождение развивает внимание, повышает мотивацию, помогает при решении более сложных тригонометрических уравнений, выделив общую идею решения: приведение уравнений к виду, содержащему лишь одну тригонометрическую функцию одного аргумента с последующей заменой переменной, или разложения на множители.
В процессе объяснения нового материала на слайдах приводятся способы решений и конечные результаты. Подробное описание урока с указанием места каждого слайда поможет успешно его провести любому учителю.
Здесь представлен конспект к уроку на тему «Решение тригонометрических уравнений», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (10 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

