Конспект урока «Методы решений иррациональных уравнений» по алгебре для 10 класса
Сивак Светлана Олеговна
Урок – игра
«Методы решений иррациональных уравнений»
Открытый урок по алгебре и началам анализа.
«Метод решения хорош, если с самого начала мы
можем предвидеть – и впоследствии подтвердить
что, следуя этому методу, мы достигнем цели».
Лейбниц.
Данный урок проводился в 10 классе с расширенным изучением математики как заключительный урок по теме «Иррациональные уравнения». Продолжительность – 2 урока (спаренных)
Цели и задачи урока:
-
Образовательные:
-
Обобщить и систематизировать знания учащихся по теме «Решение иррациональных уравнений различными методами.
-
Повторить графики различных функций
-
Повторить понятие равносильности
-
Повторить решение уравнений с параметрами
-
Развивающие:
-
развивать умение находить нужный метод при решении конкретной задачи
-
Развивать логическое мышление учащихся
-
Развивать умение учащихся говорить.
-
Формировать приемы самоконтроля при решении задач
-
Формировать правильную самооценку своего уровня освоенности предметного материала.
-
Способствовать развитию умения делать выводы
Оборудование:
-
Доска (меловая или интерактивная)
-
Чертежи
-
Бланки с раздаточным материалом
План урока:
-
Организационный момент
-
Проверка домашнего задания
-
Устная работа
-
Работа по готовым чертежам
-
Решение уравнений
-
Постановка домашнего задания
-
Подведение итогов урока и выставление оценок
Описание урока:
1. Организационный момент
Перед началом урока класс делится на 5-6 групп. Учитель вкратце объясняет учащимся правила игры и знакомит их с целями, которые должны быть достигнуты в ходе ее проведения.
2. Проверка домашнего задания
Домашнее задание дается учащимся за неделю до проведения данного урока (недельное задание).
Проверка домашнего задания осуществляется в следующей форме:
Учащиеся получают бланк №1, который будет являться ключом, и бланк №2 с таблицами для записи высказывания. Вписав в таблицу-ключ ответы к уравнениям из домашнего задания, учащиеся получают буквы для высказывания.
Группы заполняют полученные бланки и подают их учителю, а затем на доске приводится правильный ответ – высказывание. Группа, выполнившая задание первой, получает дополнительный балл.
Текст домашнего задания:
1)![]()
![]()
2) ![]()
![]()
3) ![]()
![]()
4) ![]()
![]()
5) ![]()
![]()
6) ![]()
![]()
7) ![]()
![]()
8) ![]()
![]()
9) ![]()
![]()
10) ![]()
![]()
11) ![]()
![]()
12) ![]()
![]()
13) ![]()
![]()
14) ![]()
![]()
15) ![]()
![]()
16) ![]()
![]()
17) ![]()
![]()
18) ![]()
![]()
19) ![]()
![]()

«Отгадай фразу» (На доске зашифровано высказывание из ответов домашнего задания)
Ключ:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | |
| | А | В | Д | Е | З | И | К | Л | М | Н | О | П | Р | С | Т | У | Ф | Ы | Я |
| Ответ: | | | | | | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | | | | | | |
В пишите полученное высказывание
пишите полученное высказывание
| 6 | 5 | 6 | -1 | 0 | 18 | | 4 | -1 | 6 |
| 1 |
| 5 | 6 | 1 | 19 | 109 | |
| | | | | | | | | | | | | | | | | | | |
| - | -1 | 5 | | -3 | 18 | - | -1 | 2 | -4 | |
| | | | | | | | | | | |
| -3 | -4 | - | -1 |
| |
| 18 | 109 | 19 |
| 18 | 109 | 5 | - | 5 | |
| | | | | | | | | | | | | | | | | |
Замечание: если в уравнении более одного корня, то в таблицу заносится наименьший.
Правильный ответ:
«Природа формулирует свои законы языком математики»
(Галилео Галилей)
3. Устная работа
На доске написана серия уравнений. Учащимся предлагается обсудить в группах и выбрать равносильные уравнения. Та группа, которая подготовилась первой, комментирует свое решение и за каждый правильный ответ получает балл. В случае ошибки право ответить на этот вопрос предоставляется другой группе.
Задания:
1) Равносильны ли уравнения:
![]() и
и ![]() (нет ,
(нет , ![]() )
)
![]() и
и ![]() (да)
(да)
![]() (да)
(да)
![]() (нет ,
(нет , ![]() )
)
![]() (нет ,
(нет , ![]() )
)
![]() (да)
(да)
2) При каких значениях параметра уравнения равносильны:
![]() (1)
(1)
![]() (0; 1)
(0; 1)
![]() (-1)
(-1)
![]() (-1;1)
(-1;1)
![]() a
a
![]() a =0
a =0
-
Работа по готовым чертежам
На доске представлено 10 рисунков, представляющих собой графическое решение иррациональных уравнений и 8 формул иррациональных уравнений. Учащимся предлагается поставить в соответствие каждому уравнению его решение.
Команды записывают свои ответы на листах и подают учителю. За каждый правильный ответ группа получает балл.
Формулы:
1)![]()
2)![]()
3)![]()
4)![]()
5)![]()
6)![]()
7)![]()
8)![]()
Графическое решение уравнений.
рис.1 рис.6
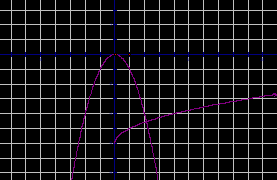
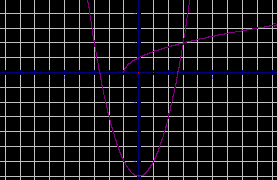
рис.2 рис.7
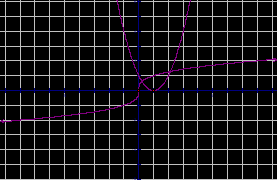
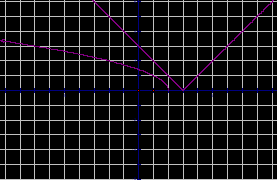
рис. 3 рис. 8
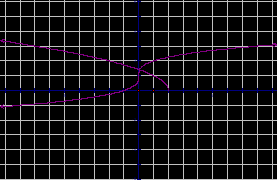
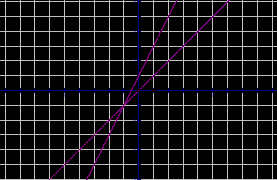
рис. 4 рис. 9
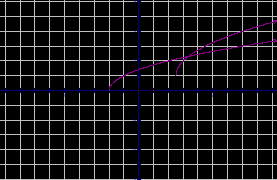
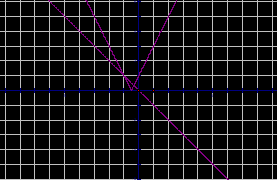
рис.5 рис.10
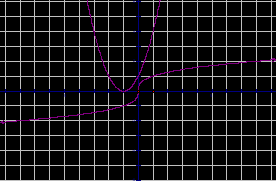
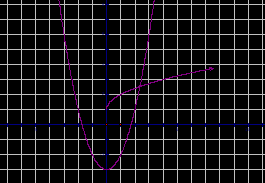
-
Решение уравнений
1)На доске появляется решение иррационального уравнения. Учитель задает вопрос «Верно ли решено уравнение?»
Учащиеся обсуждают решение в группах, а затем отвечают.
Представленное на доске решение:
2) Учащимся предлагается 10 заданий. На первом этапе группы обсуждают метод решения каждого уравнения, получая баллы за правильные ответы. Затем учитель предлагает выбрать уравнение, которое можно решить устно.(№8, монотонность). Оставшиеся уравнения распределяются между группами по жребию.
Задания:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
6. ![]()
7. ![]()
8. ![]()
9. ![]()
10. При каких значениях а график функции ![]() симметричен относительно оси Оу?
симметричен относительно оси Оу?
После того, как группы решили свои уравнения, идет обсуждение решений у доски. Группы получают баллы.
-
Постановка домашнего задания.
Те уравнения, которые не были рассмотрены на уроке остаются в качестве домашнего задания.
-
Подведение итогов урока и выставление оценок.
Здесь представлен конспект к уроку на тему «Методы решений иррациональных уравнений», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (10 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

