Конспект урока «Решение систем двух уравнений с двумя неизвестными способом подстановки» по алгебре для 7 класса
Бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа № 108»
г. Омска
КОНСПЕКТ
КОМПЕТЕНТНОСТНО-ОРИЕНТИРОВАННОГО УРОКА
по теме:
«Решение систем двух уравнений с двумя неизвестными
способом подстановки»
7 класс.
подготовила
учитель математики
Аверченко Галина Алексеевна
г. Омск
2012
Тема: «Решение систем двух уравнений с двумя неизвестными способом подстановки».
Тип урока: Постановка и решение учебной задачи (Первый урок из трех).
Обучающие цели урока:
Ученик, знающий:
1). Название способа, с помощью которого решается система двух уравнений с двумя неизвестными;
2) Формулирующий алгоритм решения системы с помощью способа подстановки, а именно:
а) выразить одну переменную через другую,
б) подставить полученное выражение во второе уравнение системы,
в) найти значение переменных,
г) записать ответ в виде пары чисел (х;у)
3) Объясняющий шаги алгоритма решения системы способом подстановки;
4) Приводящий примеры на применение алгоритма
5) Решающий системы двух уравнений с двумя неизвестными способом подстановки.
На данном уроке я продолжаю отрабатывать такие компетенции, которые прописаны в компетентностной модели выпускника школы, тем самым преследую развивающие и воспитательные цели.
Коммуникативная компетентность:
-
Владение устной коммуникацией, т.е. ученик, умеющий вести монолог, диалог, задавать вопросы, защищать свою точку зрения;
-
Владение продуктивной коммуникацией, т.е. умение работать в группе – ученик, демонстрируюший активную деятельность (организатор порядка, генератор, оформитель идей, оратор, критик).
Учебно-познавательная компетентность, т.е. ученик, умеющий логически мыслить, соотносить пройденный материал с настоящим, применять имеющиеся знания в новой ситуации, выявлять возникающие проблемы, осуществлять поиск альтернативных решений.
Методы обучения: метод взаимообучения (групповая работа), учебный диалог, дискуссия.
Педагогическая технология: проблемно-диалогическое обучение.
Используемые средства обучения: учебник «Алгебра-7» под редакцией Ш.А. Алимова и др., компьютер, проектор, экран, школьная доска.
| Деятельность учителя | Деятельность учащихся | |
| 1.Организационный (1 мин.) 2.Мотивационный (2 мин.) Стимул для КОЗ. Задачная формулировка КОЗ 3.Постановка УЗ. (5 мин.) | В нашей школе на параллели 7-х классов будет проходить математический вечер, где наряду с разными викторинами, конкурсами надо будет уметь решать задачки-игры, такие как: Один ученик загадывает два числа, говорит два условия про эти числа , а все остальные должны найти их. Давайте попробуем. Ваня загадывает числа, пишет на листочке, отдает его учителю и проговаривает условия, которым удовлетворяют эти числа. Что нужно сделать, чтобы решить эту задачу? Молодцы. Давайте запишем эту систему: 2х-у=6 - Сможете ли вы решить эту систему уравнений? - Почему? В чем затруднение? - Чем же мы будем заниматься на сегодняшнем уроке? - Как вы думаете, какова будет тема нашего урока? - Открываем тетради и записываем тему урока: Решение систем уравнений (но точку в конце предложения не ставим) | Найдите два числа, если сумма этих чисел равна 15, а разность удвоенного первого числа и второго числа равна 6. Если мы не знаем эти числа, то можно обозначить первое число Х, второе число – у. Если для этих чисел выполняются два условия, то по условию задачи нужно составить два уравнения, записать их систему и решить ее. Учащиеся записывают систему уравнений в тетради. - Нет. - Мы не знаем способа решения систем уравнений. - Искать способ решения систем уравнений. - Решение систем уравнений. Учащиеся записывают тему урока. |
| 4. Решение УЗ (20 мин.) | - Ребята, а есть ли у вас предположения о том, как решить эту систему уравнений? - Давайте проверим первую гипотезу и попробуем подобрать два числа, которые удовлетворяют обоим условиям. Учитель показывает числа, задуманные Ваней, дети видят, что решили задачу верно. - Как вы думаете, можно ли методом подбора решить любую систему? - Верно! Например, вот такую систему мы уже не сможем решить подбором: -2,5х + 1,3у = 5,8 - Значит, метод подбора не является универсальным для решения систем уравнений. Давайте проверим другую гипотезу. - Нашли ли вы решение системы уравнений? - Умеем ли мы преобразовывать уравнение так, чтобы исключить одно неизвестное? - Давайте вновь обратимся к нашей системе и попробуем исключить одну неизвестную. - Подставим полученное выражение во второе уравнение системы: - Молодцы! Вы нашли способ решения системы уравнений. А как вы думаете, какое самое важное действие мы выполняли при решении системы? - Молодцы, вы нашли ключевое слово этого метода решения – ПОДСТАВЛЯЛИ, именно поэтому данный способ решения систем равнений и называется «способ подстановки». Допишите, пожалуйста в теме урока название способа: (Решение систем уравнений способом подстановки.) Давайте вспомним пошаговую последовательность наших действий, при решении этой системы и составим общий алгоритм способа подстановки. | Работая в группах, учащиеся начинают выдвигать гипотезы по решению данной системы: - Можно попробовать подобрать решение. - Можно попытаться решить каждое уравнение системы, ведь мы умеем находить общее решение уравнения с двумя неизвестными. Учащиеся находят подбором пару чисел (7;8) которая является решением данной системы. - Наверное - нет, ведь в нашем случае система была простой, а если у неизвестных будут дробные коэффициенты, то будет уже не так просто найти решение системы. Учащиеся решают каждое равнение системы в общем виде и получают ответ: (х; 15-х) (х; 2х-6) - Нет, мы нашли решение каждого уравнения системы, но не нашли решения самой системы, значит это предположение тоже неверно. - Да. Вместо неизвестного можно подставлять в уравнение числовое значение или выражение, полученное из второго уравнения. Учащиеся работают в тетрадях и проговаривают каждый шаг решения:
х=15-у.
30-у=6 -3у=6-30 3у=24 у=8. х=15-8=7 Ответ: (7;8) - Выражали одну переменную через другую из одного уравнения и подставляли это выражение в другое уравнение. Учащиеся с помощью учителя формулируют алгоритм решения систем уравнений способом подстановки и записывают его в тетради.
|
| 5. Первичное закрепление. (4 мин.) | Один учащийся у доски решает систему с комментированием алгоритма решения систем уравнений способом подстановки. | Учащиеся в тетрадях решают систему самостоятельно и сверяют каждый шаг решения с решением написанным на доске. |
| 6. Самостоятельная работа с самопроверкой и самооценкой. (8 мин.) Решение КОЗ (на подобном примере) Инструмент проверки: модельный ответ (см. приложение) | - А сейчас самостоятельно, по вариантам решите способом подстановки систему уравнений: 1 вариант: 5х-7у=11 2 вариант: 5х-2у=9 Оценивание. 4+ - (5), 3+ - (4) 2+ - (3) 1+; 0 - (2) | Учащиеся решают в тетрадях предложенную учителем систему уравнений, сверяют решение и ответ с заранее написанным учителем (но закрытым) решением на доске. Находят ошибки в своем решении и оценивают свою работу с последующим комментированием по пунктам. Верно ли:
|
| 7. Итоговая рефлексия. Домашнее задание. (5 мин.) | - Какая проблема сегодня возникла у нас на уроке? - Какими способами мы пытались решить эту проблему? Какие затруднения возникли? - А какой результат вы получили? Ребята, давайте посмотрим, как вы сегодня работали, как хорошо вы поняли новую тему. Определите, на каком уровне знания вы находитесь: - знаю и объясню другому; - знаю, - сомневаюсь, что знаю, - не знаю. Подводится итог урока. Активно работавшим учащимся выставляются отметки. - Молодцы! Запишите, пожалуйста, домашнее задание: выучить алгоритм решения систем уравнений способом подстановки. № 136 (2,3) № 138 (2,3) Спасибо за урок. | - Мы не смогли решить систему уравнений. - Мы искали способ решения системы уравнений. Сначала мы предложили метод подбора, но выяснили, что этим способом нельзя решить любую систему, а затем мы попробовали решить каждое уравнение системы отдельно, но не смогли получить решение всей системы. - Мы нашли универсальный способ решения систем уравнений – способ подстановки и научились решать системы уравнений этим способом. Для этого надо:
Значит наш результат соответствует цели урока – научиться решать системы уравнений способом подстановки. Ребята поднимают руку на выбранный ими уровень знаний. Учащиеся в дневниках записывают домашнее задание. |
ПРИЛОЖЕНИЕ.
Самостоятельная работа.
Вариант 1.
х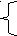 +у=7,
+у=7,
5х-7у=11;
а) х= 7-у; или а) у=7-х
б) 5(7-у)-7у=11 б) 5х-7(7-х)=11
35 – 5у – 7у =11 5х-49+7х=11
-12у=11-36 12х=60
-12у= -24 х=5
у=2
в) х=7-2=5 в)у=7-5=2
г) (5;2) г) (5;2)
Вариант 2.
х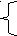 +у=6,
+у=6,
5х-2у=9;
а) х = 6-у; или а) у=6-х
б) 5(6-у)-2у=9; б) 5х-2(6-х)=9
30 – 5у – 2у =9; 5х-12+2х=9
-7у=-21; 7х=21
у=3; х=3
в) х=6-3=3; в)у=6-3=3
г) (3;3). г) (3;3)
Список литературы.
-
Алгебра: Учеб. Для 7 кл. общеобразоват. учреждений / Ш.А.Алимов и др. – М.: Просвещение, 2000.
-
Материалы Телекоммуникационного обучающего проекта-конкурса
для учителей, аспирантов, магистрантов педагогических вузов
«Компетентностно-ориентированный урок».
Здесь представлен конспект к уроку на тему «Решение систем двух уравнений с двумя неизвестными способом подстановки», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (7 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

