Конспект урока «Построение графика квадратичной функции» по алгебре для 9 класса
Учитель: Рогачева Татьяна Викторовна
Место работы: ГОУ СОШ №103, Санкт-Петербург
Должность: Учитель математики
Урок алгебры в 9 классе
«Построение графика квадратичной функции»
Тип урока: урок усвоения новых знаний.
Технология: работа в малых группах.
Дидактическое сопровождение: карточки с заданиями
Оборудование: проекционный аппарат
ХОД УРОКА
-
Актуализация опорных знаний
Фронтальный опрос:
-
Какая функция называется квадратичной?
-
Какой из рисунков, изображенных на доске(или экране) не является графиком квадратичной функции?
-
Как называется график квадратичной функции?
-
Является ли парабола симметричной фигурой?
-
Что такое ось симметрии?
-
Что такое вершина параболы?
-
Что такое нули функции?
-
Сколько точек пересечения может иметь парабола с осями ОХ и ОУ?
-
Сообщение темы урока
Тема: Построение графика квадратичной функции у = ах2 +bх +с
Цель:
Образовательная:
-
Исследовать положение графика квадратичной функции у = ах2 +bх +с в зависимости от а, b, с;
-
Разобрать алгоритм построения графика квадратичной функции;
-
Научиться применять его на практике;
-
Закрепить навык построения графика квадратичной функции, заданной формулой у = ах2 +bх +с, где а, b, с – заданные действительные числа, а≠0, х – действительная переменная;
-
Закрепить навык построения графика квадратичной функции, заданной формулой у = а (х – х0)2 + у0;
Развивающая:
-
Развивать умение работать в группе;
-
Развивать умение определять цели деятельности на уроке;
-
Развивать умение правильно организовать свою работу по достижению поставленной цели;
Воспитательная:
-
Воспитывать трудолюбие, добросовестность, честность.
-
Воспитывать стремление прийти на помощь товарищу.
-
Усвоение новых знаний
Учащиеся класса работают в группах или парах, а учитель проводит индивидуальную работу (при необходимости) с теми учениками, у которых умения и навыки по данной теме сформированы ещё не достаточно.
Задание №1.
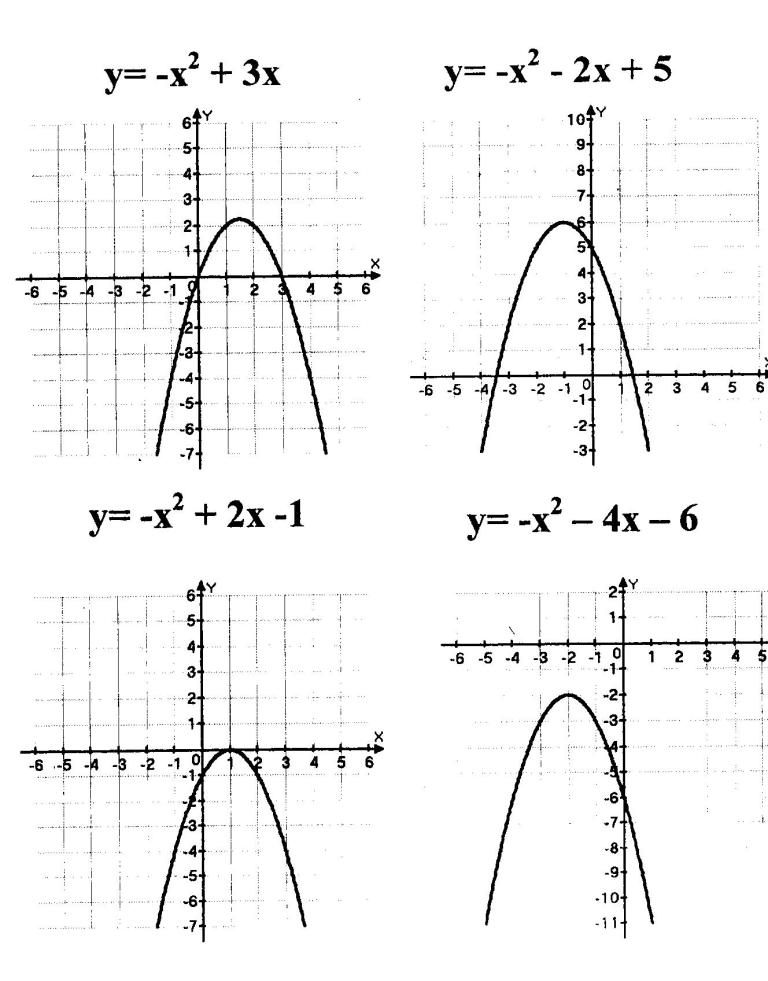
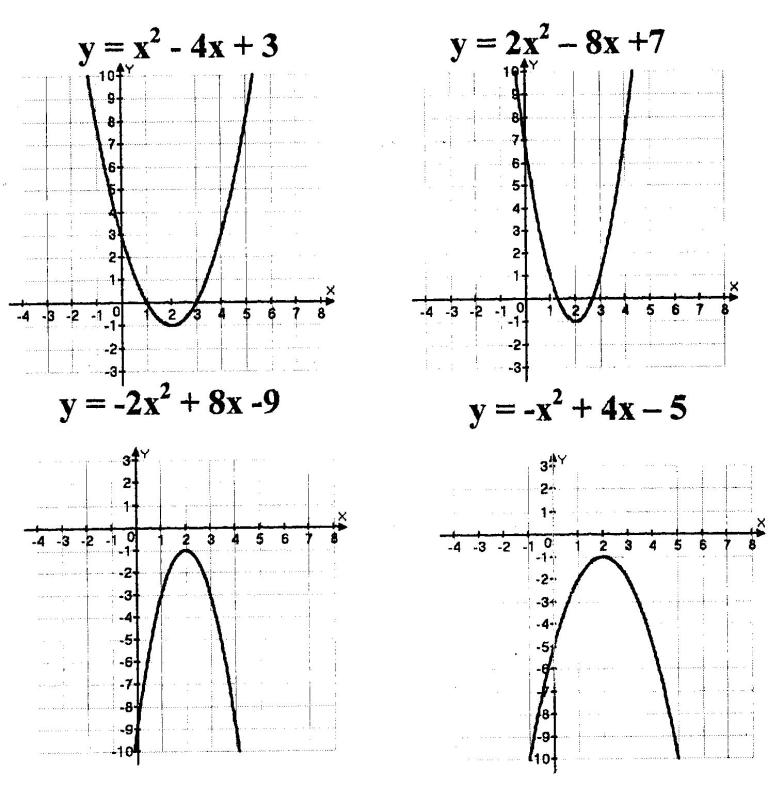
Каждая группа получает комплект из 4 карточек с изображенными на них графиками и их формулами (Приложение №1).
Задание:
-
Каждый записывает, чему равны а,b, с для его формулы;
-
Работая в паре, сравнивают записанные значения (величину и знаки) и находят общее.
-
Сравнивают внешний вид графиков (направление ветвей параболы, положение вершины, точки пересечения с осями) и находят общее.
-
Записывают вывод.
-
Меняются карточками и работают в новой паре по п.1-4
-
Готовятся к выступлению от группы с выводами о связи внешнего вида графиков и коэффициентов а, b, с.
-
Графики, выданные каждой группе, проецируются на экран через проектор мультимедиа..
-
Заслушиваются выступления представителей каждой группы.
Учитель подводит итог.
Задание №2.
На экран проецируются 4 графика (Приложение №2).
Необходимо определить знаки коэффициентов параболы у = ах2 +bх +с (по очереди представители каждой группы).
Учитель оценивает ответ, обсуждая с учащимися.
Задание №3.
-
Каждый получает схему построения графика квадратичной функции и карточку с формулой.
-
Работают в паре.
-
Первый читает схему по пунктам.
-
Второй выполняет построение, объясняет.
-
Первый проверяет.
-
Второй читает схему по пунктам.
-
Первый выполняет построение, объясняет.
-
Второй проверяет.
-
Проверяют построенный график, сверяя с образцом.
-
Меняются карточками.
-
Первый строит график функции по формуле, заданной в новой карточке, используя схему построения.
-
Объясняет построение.
-
Второй слушает, и проверяет, сверяя со своим построением.
-
Второй строит график функции по формуле, заданной в новой карточке, используя схему построения.
-
Объясняет построение.
-
Первый слушает, и проверяет, сверяя со своим построением.
-
Приступают к работе в новой паре. Повторяются п.10-17.
Работа продолжается, пока каждый не построит все графики.
Учитель контролирует работу малых групп.
Задание №4
Каждый учащийся получает карточку с формулой и строит график самостоятельно. (Приложение 3)
Преобразовывает формулу у = ах2 +bх +с, используя метод выделения полного квадрата, в формулу у = а(х – х0)2 + у0, где х0, у0 – координаты вершины параболы.
Создаются новые малые группы в зависимости от цвета карточки.
Работа в паре. Обсуждают, с помощью какого трафарета можно построить график и как переместить этот трафарет вдоль осей ОХ и ОУ, чтобы получить данный график. Выступление от групп.
Дополнительное задание.
С помощью шаблона параболы у = х2 построить графики функций:
У = -(х – 1)2 – 3;
У = (х + 2)2 + 1;
У = - (х – 3)2 + 2;
У = (х + 4)2 – 5.
-
Итог урока.
-
Что узнали нового?
-
Чему учились?
-
Чему научились?
Обсуждаем работу групп. Выставляем оценки.
-
Домашнее задание.
Идет инструктаж домашнего задания.
Задания должны быть на построение графиков квадратичной функции.
§2, п.5 п.6 №80, №90.
Литература.
-
Ю.Н. Макарычев, Н.Г.Миндюк, К.И.Нешков Алгебра, учебник для 9 класса с углубленным изучением математики, Мнемозина, 2004г.
-
http://www.ptank.com/blog/2006/09/the-logistic-function-and-its-discontents/ парабола
Инструкция для работы в парах сменного состава
1 2 1 2





Задание №1.
Достать из зеленой папки комплект из 4 карточек с изображенными на них графиками и их формулами и раздать их.
-
Записать, чему равны а, b, с.
-
Работая в паре, сравнить записанные значения (величину и знаки) и найти общее.
-
Сравнить внешний вид графиков (направление ветвей параболы, положение вершины, точки пересечения с осями) и найти общее.
-
Записать вывод.
-
Поменяться карточками и начать работу по п.1-5.
-
Подготовить выступление от группы с выводами о связи внешнего вида графиков т одного из коэффициентов а, b, с.
-
Графики, выданные каждой группе, проецируются через проектор мультимедиа на экран.
-
Выступает один из представителей группы.
Задание №2.
На экран проецируются графики функций.
Назвать знаки a,b, и значение c для данных графиков (по очереди представители каждой группы).
Задание №3.
Д

 остать из красной папки план построения графика квадратичной функции и карточку с формулой.
остать из красной папки план построения графика квадратичной функции и карточку с формулой.
-
2



1 2
Работать в паре.
-
Первый читает пункт 1 плана второму. Второй выполняет, объясняет. Аналогично продолжается работа пары по всем остальным пунктам плана.
-
Второй читает пункт 1 плана первому. Первый выполняет, объясняет. Второй проверяет. Аналогично продолжается работа пары по всем остальным пунктам плана.
-
Из папки синего цвета достать карточку, совпадающую по цвету с карточкой задания. Проверить построенный график, сверяя с образцом.
-
Обменяться карточками.
-
Первый строит график по формуле, заданной в новой карточке, используя схему построения. Объясняет построение. Второй слушает и проверяет, сверяя со своим построением.
-
Второй строит график функции по формуле, заданной в новой карточке, используя схему построения. Объясняет построение. Первый слушает и проверяет, сверяя со своим построением.
-
Приступить к работе в новой паре. Повторить п.4-6. Выполнить построение в новой координатной плоскости.
Работа продолжается, пока каждый не построит все 4 графика.
Задание №4.
Достать карточки с заданием из папки желтого цвета.
-
Построить график по схеме самостоятельно. Преобразовывает формулу у = ах2 +bх +с, используя метод выделения полного квадрата, в формулу у = а(х – х0)2 + у0, где х0, у0 – координаты вершины параболы.
-
Создать новые малые группы. Объединившись по цвету карточек.
-
Найти портнера с одинаковым заданием. Сверить построенные графики и полученные формулы.
-
Достать шаблоны функций из оранжевой папки.
-
Работая в паре, обсудить, с помощью какого трафарета можно было построить полученный график и как переместить вдоль осей ОХ и ОУ, чтобы получить этот график.
-
Сделать вывод, как построить график квадратичной функции, заданной формулой у=а(х – х0)2 + у0, используя трафарет.
Дополнительное задание.
При помощи трафарета построить на одной координатной плоскости графики, достав формулы из фиолетовой папки.
Приложение 2.
-
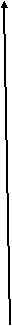
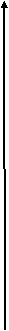 у 3. у
у 3. у
х х

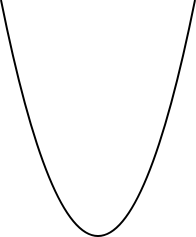
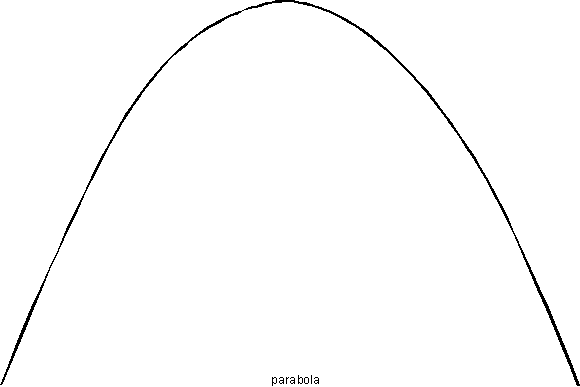
-
 у 4. у
у 4. у
х х



Приложение 3.
Карточки для 4 задания
(по 2 штуки)
Красная карточка Красная карточка
У = - 2х2 + 8х – 6 У = х2 - 6х + 10
Зеленая карточка Зеленая карточка
У = 2х2 + 8х + 10 У = - х2 - 6х – 8
Синяя карточка Синяя карточка
У = 2х2 + 4х – 6 У = - х2 - 2х – 3
Желтая карточка Желтая карточка
У = - 2х2 + 8х – 9 У = х2 - 6х + 8
Приложение 1.
Задание №1
1 группа
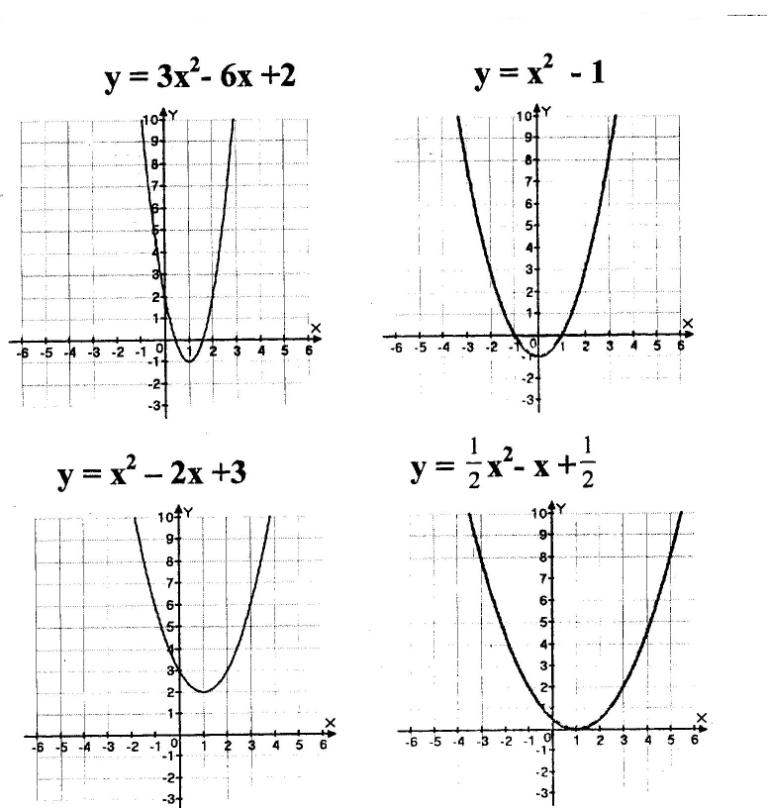
Задание №1
Группа 2.
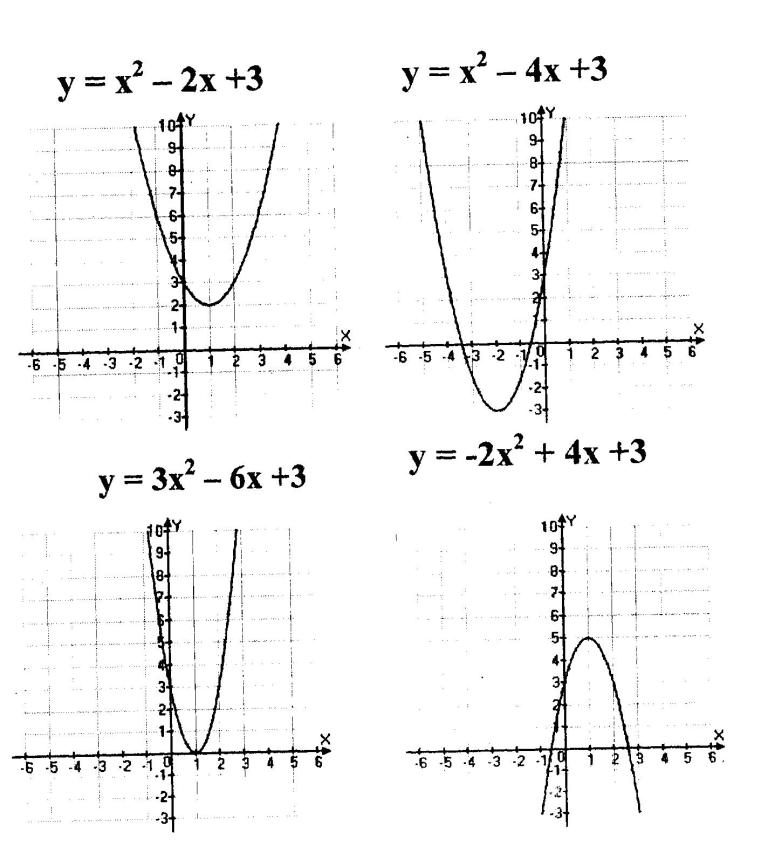
Задание №1
-
группа
Задание №1
Группа 4.
Здесь представлен конспект к уроку на тему «Построение графика квадратичной функции», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (9 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

