Конспект урока «Тождественные преобразование выражений» по алгебре для 7 класса
План - конспект урока
Тышибаева Нуржамал Шахмановна,
учитель математики,
г.Астана, СШ № 13
Класс: 7 «А»
Предмет: алгебра
Дата проведения: 5.01.2014
Тема урока: Тождественные преобразование выражений.
Цель:
1)закрепить умение применять формулы сокращенного умножения при преобразований выражений.
2)развивать логическое мышление, математическую речь, память, внимания.
3) воспитывать способность самореализации учащихся, прививать навыки самостоятельной работы.
Тип урока: урок повторения ,обобщения и систематизация пройденного материала
Оборудование: интерактивная доска, раздаточный материал для учащихся, презентация к уроку.
Ход урока:
1.Организационный момент:(1мин)
1)Психологический настрой (скажите друг другу пожелание)
2.Проверка домашнего задания(1мин).
(проверяю наличие домашнего задания)
3.Устный счет(5 мин)
Замените * одночленом так, чтобы получившееся равенство было тождеством.
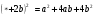
a
2m
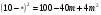 3b
3b
0,4 y
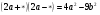 x2, y2
x2, y2
x3, 64
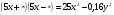 .
.
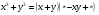
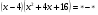
4.Повторение формул сокращенного умножения(5 мин)
Установите соответствие
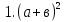 А)
А)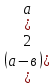
2.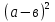 Б) (а-в)(а+в)
Б) (а-в)(а+в)
3.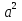 -
-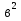 В)
В)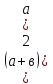
4.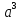 +
+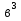 Г)
Г)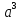 +3
+3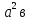 +3а
+3а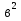 +
+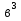
5.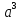 -
-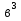 Д)
Д) 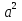 +2ав+
+2ав+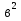
6.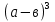 Е)
Е)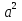 -2ав+
-2ав+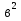
7. 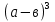 Ж)
Ж) 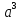 -3
-3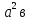 +3а
+3а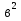 -
-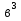
5.Самостоятельная работа с взаимопрверкой по вариантам(5 мин)
-
Ответы: I вариант
-
x - 2)2 = x2 - 4x + 4
-
(2x + 3y)2 = 4х2 + 12xy + 9y2
-
(a + 2b)(a - 2b) =а2 - 4b2
-
(a + 3)3 = a3 + 3a23 + 3a32 + 33 = a3 + 9a 2+ 27a + 27
-
Ответы:II вариант
-
(x + 3)2 = x2 + 6x + 9
-
(4x - 2y)2 = 16x2 - 16xy + 4y2
-
4а2 – b2 = (2a - b)(2a + b)
-
(a - 3)3 = a3 - 3a 2 3 + 3a32 – 33 =a3 - 9a2 + 27a- 27
6.Работа с учебником у доски +со слабоуспевающими( карточки)(10мин)
№225(2)
№226(1,3)
7.Самостоятельная работа по уровням(А,В,С)(15мин)
Уровень А
Вариант 1.
-
Разложите на множители: а) c2 – a2 ; б) 1 - n2; в) p2 – n2 ; г) b2 – 4.
-
Разложите на множители: а) а3 + b3; б) р3 - к3. в) с3 + 8; г)у3 - 125.
-
Выполните действия: а) (х - 3)(х + 3); б) (х - 3)2; в) (х - 3)(х - 4).
Вариант 2.
-
Разложите на множители: а) x2 – k2 ; б)1 - b2; в)b2 – y2 ; г) x2 – 64.
-
Разложите на множители: а) с3 - р3, б) b3 + х3. в) 64 - а3 ; г) к3 - 125.
-
Выполните действия: а)(6 + а)2; б) (6 +а)(6 - а); в)(6 + а)(5 - а).
Вариант 3.
-
Разложите на множители: а) c2 – x2 ; б)1 - p2; в) x2 – b2 ; г) y2 – 36.
-
Разложите на множители: а) р3 + х3; б)х3 - у3. в) 27 + р3 ; г) у3 - 8.
-
Выполните действия: а) (с - 5)2; б)(с - 5)(с + 5); в) (с - 6)(с + 8).
Вариант 4.
-
Разложите на множители: а) k2 – y2 ; б)1 - p2; в)y2 – c2 ; г) b2 – 9.
-
Разложите на множители: а)y3 + a3; б) n3 - k3. в)125 - к3 ; г) а3 - 27.
-
Выполните действия: а) (р + 2)(р - 2); б) (р + 2)(р - 3); в) (р + 2)2.
Уровень В
Вариант 5.
-
Упростите: а) (с + х) 2+ (с - х)2; б) (р + 7)2 + (р - 6)2.
-
Упростите: а) (5а + b) 2 - 25а2, б) (1 - 8с)2 + 16с.
-
Вычислите: а) 962 – 862; б) 1262 – 742; в) 0,9782 – 0,0782.
Вариант 6.
-
Упростите: а) (в + у) 2+ (в - у)2; б) (а + 8)2 + (а - 8)2.
-
Упростите: а)(6х + 5) 2 - 36х2; б) (1 - 9р)2 + 18р.
-
Вычислите: а) 7772 – 7672; б) 1492 – 512; в) 0,6382 – 0,3622.
Вариант 7.
-
Упростите: а) (х + у) 2+ (х - у)2; б) (а + 4)2 + (а - 4)2.
-
Упростите: а) (2х + у) 2 - 4х2; б) (1 - 5а)2 + 10а.
-
Вычислите: а) 822 – 722; б) 1652 – 352; в) 0,3852 – 0,6152
Вариант 8.
-
Упростите: а) (к + р) 2+ (к - р)2; б) (а + 9)2 + (а - 9)2.
-
Упростите: а) (7а + у) 2 - 49а2; б) (1 - 4с)2 + 8с.
-
Вычислите: а) 632 – 532; б) 1442 – 562; в) 0,5282 – 0,4722.
Уровень С
Вариант 9.
-
Упростите: а) 2х(2х + у) + (1 - 2х) 2; б) а(а + 3b) - (а – 3b)2.
-
Упростите: а) (b - с)(b - 5с)+(b - 6с)2; б) 4(а + b)2 - 2(a - b)2.
-
Решите уравнение: (12x - 4)(12x + 4) - (12x – )2 – (4x – 5) = 4.
Вариант 10.
-
Упростите: а) 7у(7у + р) + (1 - 7у)2; б) х(х + 8у) - (х - 8у)2.
-
Упростите: а) (у - к)(у - 3к)+(к - 4у)2; б) 6(р + х)2 - 2(р - х)2.
-
Решите уравнение: (7x - 8)(7x + 8) - (25x – 4)2 + 36(1 – 4x)2 =44
Вариант 11.
-
Упростите: 3у(3у + с) + (1 - 3у)2; b(b + 4с) - (b - 4с)2.
-
Упростите: (к - р)(к - 7р) + (к- 7р)2; 5(а + х)2 - 3(a - х)2.
-
Решите уравнение:(9y - 4)2+ (40y + 1)2 - (41y - 2)(41y + 2)=25.
Вариант 12.
-
Упростите: 8с(2с + х) + (1 - 2с)2; с(с + 5р) - (с - 5р).
-
Упростите: (а - b)(а – 2b) + (2а - b)2; 3(х + у)2 - 2(х - у)2.
-
3.Решите уравнение: (20 - x)2+ (21x + 2)2 - (29x - 3)(29x + 3) = 3
8.Д/З: Решить тестовые задания на стр.84(1мин)
9.Итог урока(2мин):
Сегодня я на уроке повторил…………..
Сегодня я на уроке научился…………….
Сегодня я на уроке узнал…………………
Здесь представлен конспект к уроку на тему «Тождественные преобразование выражений», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (7 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

