Конспект урока «Тригонометрические уравнения» по алгебре
Захарова Людмила Владимировна
МБОУ «Средняя общеобразовательная школа № 59» г. Барнаула
учитель математики
zlv-13@mail.ru
№1 Простейшие тригонометрические уравнения
Цель: 1. Вывести формулы решений простейших тригонометрических уравнений вида sinx =a, cosx=a, tgx=a, ctgx=a;
2. Научиться решать простейшие тригонометрические уравнения с помощью формул.
Оборудование: 1)Таблицы с графиками тригонометрических функций у=sinx, у=cosx, у=tgx, у=ctgx; 2)Таблица значений обратных тригонометрических функций; 3)Сводная таблица формул для решения простейших тригонометрических уравнений.
План урока-лекции:
1.Вывод формул корней уравнения
а) sinx =a,
б) cosx=a,
в) tgx=a,
г) ctgx=а.
2. Устная фронтальная работа по закреплению полученных формул.
3. Письменная работа по закреплению изученного материала
Ход урока.
В алгебре, геометрии, физике и других предметах мы сталкиваемся с разнообразными задачами, решение которых связано с решением уравнений. Мы изучили свойства тригонометрических функций, поэтому естественно обратиться к уравнениям, в которых неизвестное содержится под знаком функций
Определение: Уравнения вида sinx =a, cosx=a, tgx=a, ctgx=а называются простейшими тригонометрическими уравнениями.
Очень важно научиться решать простейшие тригонометрические уравнения, так как все способы и приемы решения любых тригонометрических уравнений заключается в сведении их к простейшим.
Начнем с того, что выведем формулы, которые «активно» работают при решении тригонометрических уравнений.
1.Уравнения вида sinx =a.
Решим уравнение sinx =a графически. Для этого в одной системе координат построим графики функций у=sinx и у=а.
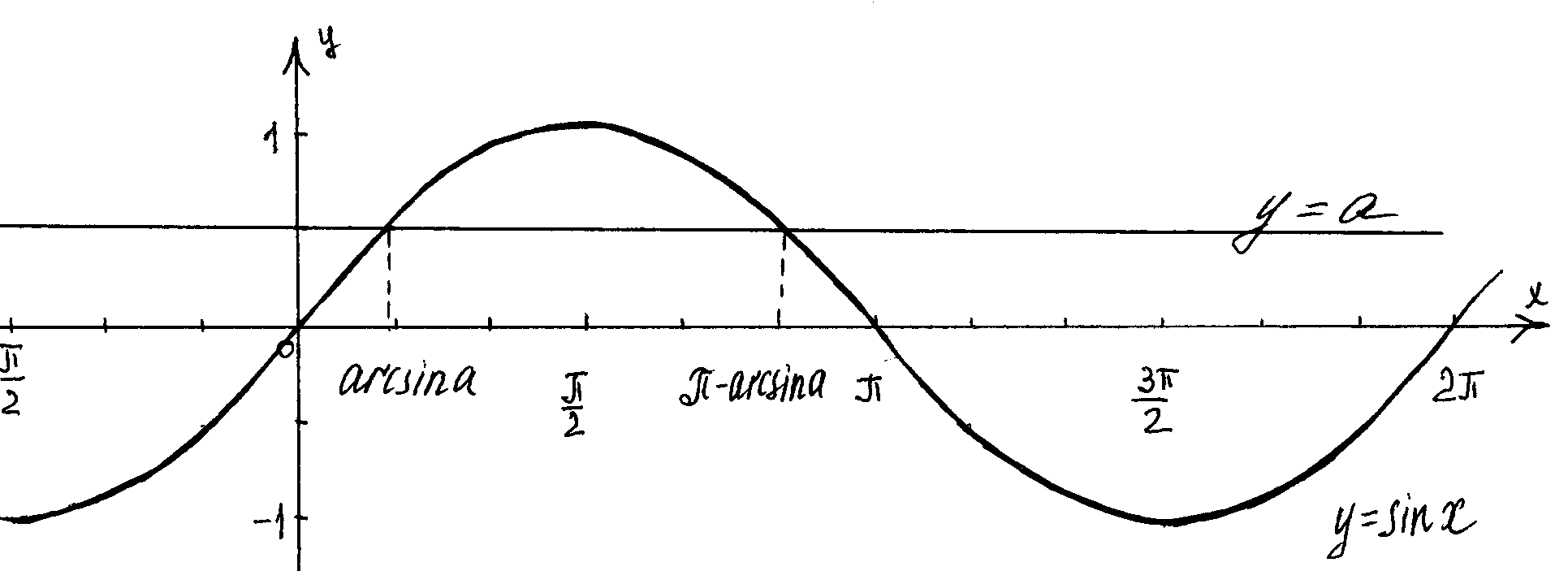
1) Если а> 1 и аsinх=а не имеет решений, так как прямая и синусоида не имеют общих точек.
2) Если -1а а пересечет синусоиду бесконечно много раз. Это означает, что уравнение sinx=a имеет бесконечно много решений.
Так как период синуса равен 2![]() , то для решения уравнения sinx=a достаточно найти все решения на любом отрезке длины 2
, то для решения уравнения sinx=a достаточно найти все решения на любом отрезке длины 2![]() .
.
Решением уравнения на [-![]() /2;
/2; ![]() /2] по определению арксинуса х=arcsin a, а на [
/2] по определению арксинуса х=arcsin a, а на [![]() /2; 3
/2; 3![]() /2] х=
/2] х=![]() -arcsin a. Учитывая периодичность функции у=sinx получим следующие выражения
-arcsin a. Учитывая периодичность функции у=sinx получим следующие выражения
x=arcsin a+ 2![]() n
n
х= ![]() -arcsin a+2
-arcsin a+2![]() n, n
n, n![]() Z.
Z.
Обе серии решений можно объединить
х= ( -1)narcsin a+![]() n, n
n, n![]() Z.
Z.
В следующих трех случаях предпочитают пользоваться не общей формулой, а более простыми соотношениями:
Если а=-1, то sin x =-1, х=-![]() /2+2
/2+2![]() n
n
Если а=1, то sin x =1, x =![]() /2+2
/2+2![]() n
n
Если а=0, то sin x =0. x = ![]() n,
n,
Пример: Решить уравнение sinx =1/2.
Составим формулы решений x=arcsin 1/2+ 2![]() n
n
х= ![]() -arcsin a+2
-arcsin a+2![]() n
n
Вычислим значение arcsin1/2. Подставим найденное значение в формулы решений
x=![]() /6+ 2
/6+ 2![]() n
n
х= 5![]() /6+2
/6+2![]() n
n
или по общей формуле
х= ( -1)narcsin 1/2+![]() n,
n,
х= ( -1)n![]() /6+
/6+![]() n,
n,
2. Уравнения вида cosx=a.
Решим уравнение cosx=a также графически, построив графики функций у= cosx и у=а.
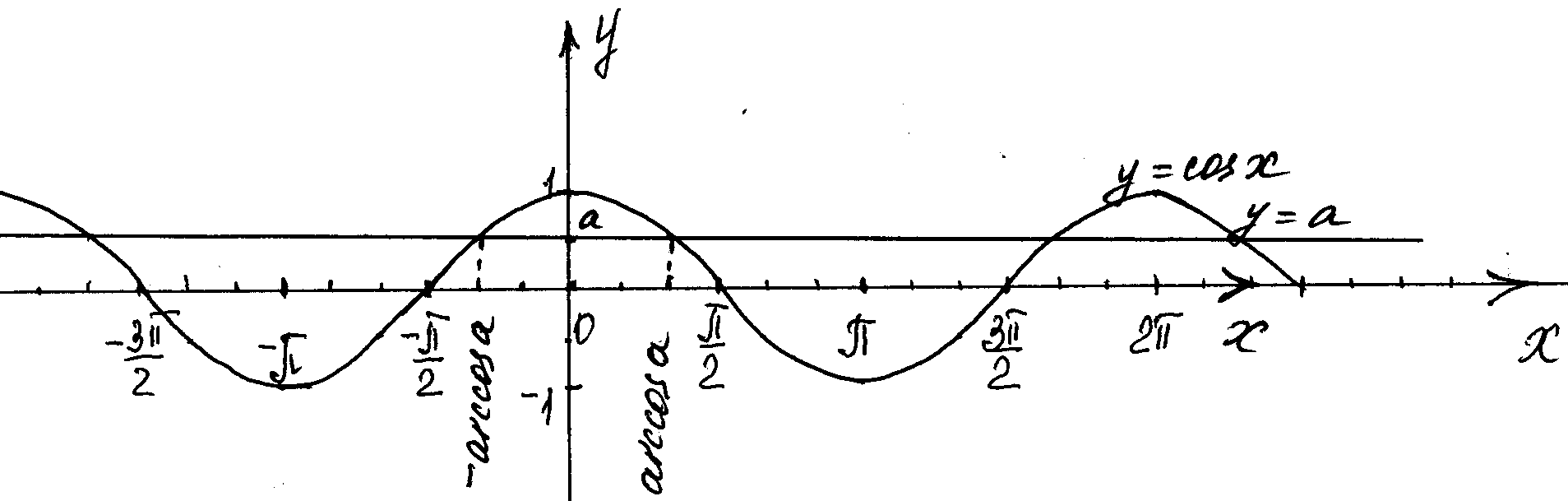
1) Если а 1, то уравнение cosx=a не имеет решений, так как графики не имеют общих точек.
2) Если -1acosx=a имеет бесконечное множество решений.
Найдем все решения cosx=a на промежутке длины 2![]() так как период косинуса равен 2
так как период косинуса равен 2![]() .
.
На [0; ![]() ] решением уравнения по определению арккосинуса будет х=arcos a. Учитывая четность функции косинус решением уравнения на [-
] решением уравнения по определению арккосинуса будет х=arcos a. Учитывая четность функции косинус решением уравнения на [-![]() ;0] будет х=-arcos a.
;0] будет х=-arcos a.
Таким образом решения уравнения cosx=a х=+ arcos a+2 ![]() n,
n,
В трех случаях будем пользоваться не общей формулой, а более простыми сотношениями:
Если а=-1, то cosx =-1, x =-![]() /2+2
/2+2![]() n
n
Если а=1, то cosx =1, x = 2![]() n,
n,
Если а=0, то cosx =0. x =![]() /2+
/2+![]() n
n
Пример: Решить уравнение cos x =1/2,
Составим формулы решений x=arccos 1/2+ 2![]() n
n
Вычислим значение arccos1/2.
Подставим найденное значение в формулы решений
X=+ ![]() /3+2
/3+2![]() n, n
n, n![]() Z.
Z.
-
Уравнения вида tgx=a.
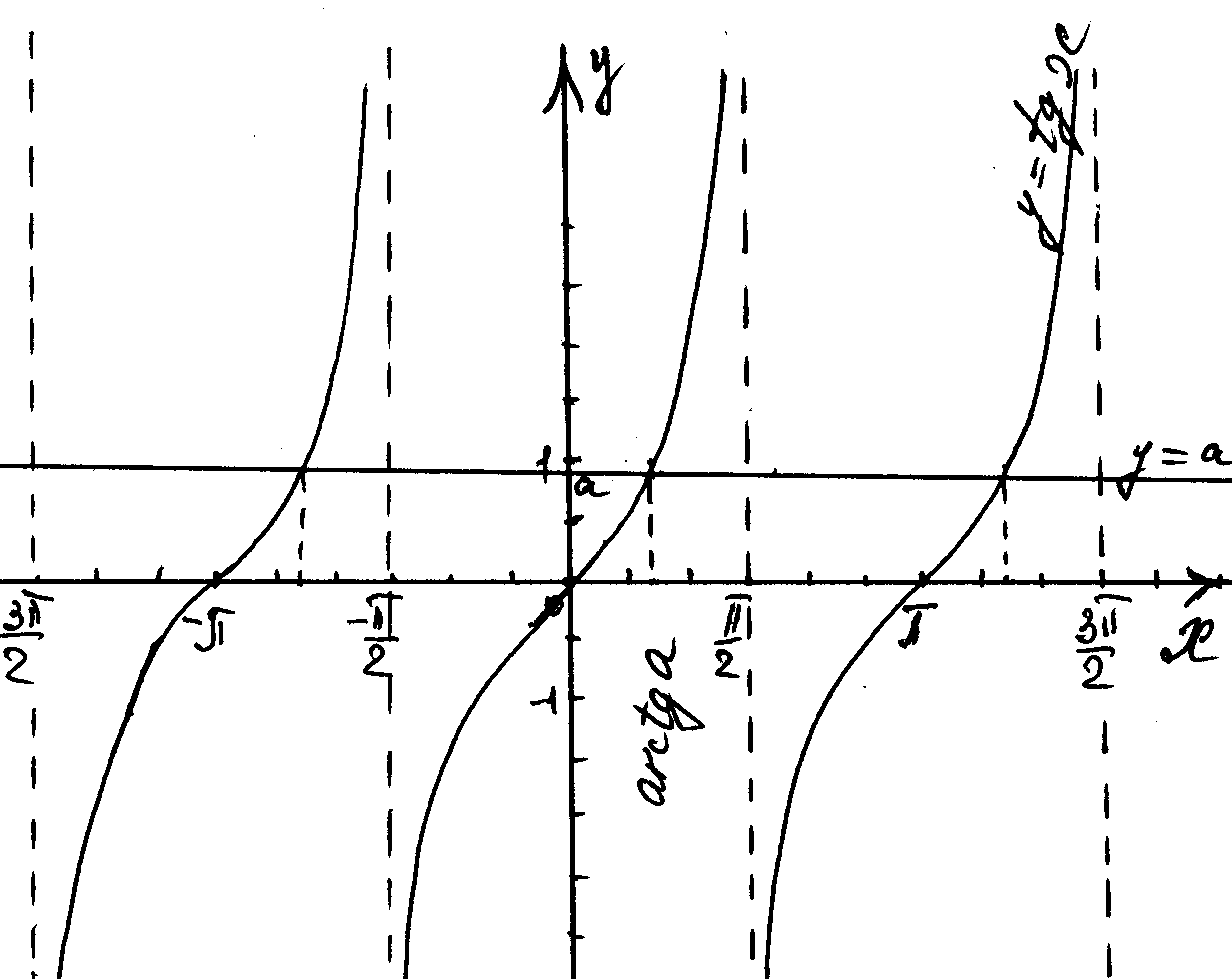
Так как период тангенса равен ![]() , то для того чтобы найти все решения уравнения tgx=a, достаточно найти все решения на любом промежутке длины
, то для того чтобы найти все решения уравнения tgx=a, достаточно найти все решения на любом промежутке длины ![]() . По определению арктангенса решение уравнения на (-
. По определению арктангенса решение уравнения на (-![]() /2;
/2; ![]() /2) есть arctga. Учитывая период функции все решения уравнения можно записать в виде
/2) есть arctga. Учитывая период функции все решения уравнения можно записать в виде
х= arctg a+ ![]() n, n
n, n![]() Z.
Z.
Пример: Решите уравнение tg x = 3/3
Составим формулу для решения х= arctg 3/3 +![]() n, n
n, n![]() Z.
Z.
Вычислим значение арктангенса arctg 3/3= ![]() /6, тогда
/6, тогда
х=![]() /6+
/6+![]() n, n
n, n![]() Z.
Z.
Вывод формулы для решения уравнения сtgx=a можно предоставить учащимся.
Пример.
Решить уравнение ctg х = 1.
х = arcсtg 1 + ![]() n, n
n, n![]() Z,
Z,
х = ![]() /4 +
/4 + ![]() n, n
n, n![]() Z.
Z.
В результате изученного материала учащиеся могут заполнить таблицу:
«Решение тригонометрических уравнений».
| формулы корней | |
| sinx =a | х= ( -1)narcsin a+ |
| cosx=a | х=+ arcos a+2 |
| tgx=a | х= arctg a+ |
| сtgx=a | х= arcсtg a+ |
Упражнения для закрепления изученного материала.
-
(Устно ) Какие из записанных уравнений можно решить по формулам:
а) х= ( -1)narcsin a+![]() n, n
n, n![]() Z;
Z;
б) х=+ arcos a+2 ![]() n?
n?
cos x = 2/2, tg x= 1 , sin x = 1/3, ctg x = 3/3, sin x = -1/2, cos x= 2/3, sin x = 3 , cos x = 2.
Какие из перечисленных уравнений не имеют решений?
-
Решите уравнения:
а) sin x = 0; д) sin x = 2/2; з) sin x = 2;
б) cos x = 2/2; е) cos x = -1/2; и) cos x = 1;
г) tg x = 3; ж) ctg x = -1; к) tg x = 1/ 3.
3. Решите уравнения:
а) sin 3x = 0; д) 2cos x = 1;
б) cos x/2 =1/2; е) 3 tg 3x =1;
г) sin x/4 = 1; ж) 2cos(2x+ ![]() /5) = 3.
/5) = 3.
При решении данных уравнений полезно записать правила для решения уравнений вида sinвx =a, и сsinвx =a, |a|1.
| cosвx=a, |a|1. вx=+ arcos a+2 х=+ 1/вarcos a+2
| |
| сsinвx =a, |a|1. sinвx =a/с, вх= ( -1)n arcsin a/с+ х= ( -1)n1/в arcsin a/с+ | с cos вx =a, |a|1. cos вx =a /с/. X=+ 1/в arcos a/с+2 |
Подведение итогов занятия:
-
Сегодня на занятии мы вывели формулы для решения простейших тригонометрических уравнений.
-
Разобрали примеры решения простейших тригонометрических уравнений.
-
Заполнили таблицу, которую будем использовать для решения уравнений.
Домашнее задание.
№2 Решение тригонометрических уравнений
Цель: Изучить методы решения тригонометрических уравнений:1) приводимых к квадратным;2) приводимых к однородным тригонометрическим уравнениям.
Развивать у учащихся наблюдательность при применении различных способов решения тригонометрических уравнений.
-
Фронтальная работа с учащимися.
-
Назовите формулы корней тригонометрических уравнений cos x=a, sin x=a, tgx = a, ctg x = a.
-
Решите уравнения (устно):
cos x=-1, sin x=0, tgx =0, ctg x=1, cos x=1,5, sin x=0.
-
Найдите ошибки и подумайте о причинах ошибок.
cos x=1/2, х=+![]() /6+2
/6+2![]() k, k
k, k![]() Z.
Z.
sin x= 3/2, х= ![]() /3+
/3+![]() k, k
k, k![]() Z.
Z.
tgx = ![]() /4, x=1+
/4, x=1+ ![]() k, k
k, k![]() Z.
Z.
2. Изучение нового материала.
На данном занятии будут рассмотрены некоторые наиболее часто встречающиеся методы решения тригонометрических уравнений.
Тригонометрические уравнения, приводимые к квадратным.
К этому классу могут быть отнесены уравнения, в которые входят одна функция (синус или косинус) или две функции одного аргумента, но одна их них с помощью основных тригонометрических тождеств сводится ко второй.
Например, если cоsх входит в уравнение в четных степенях, то заменяем его на 1- sin2x, если sin2x, то его заменяем на 1-cos2x.
Пример.
Решить уравнение: 8sin2x - 6sin x -5 =0.
Решение: Обозначим sin x=t, тогда 8t2- 6t – 5=0,
D= 196,
t1= -1/2, t2= -5/4.
Выполним обратную замену и решим следующие уравнения.
sin x= -1/2,
х=(-1)к+1![]() /6+
/6+![]() k, k
k, k![]() Z.
Z.
sin x= -5/4.
Так как -5/4>1, то уравнение не имеет корней.
Ответ: х=(-1)к+1![]() /6+
/6+![]() k, k
k, k![]() Z.
Z.
Решение упражнений на закрепление.
Решить уравнение:
1) 2sin2 x+ 3cos x = 0;
2) 5sin2 x+ 6cos x -6 = 0;
3) 2sin2 x+ 3cos2 x = -2sin x;
4) 3tg 2x +2 tgx-1=0.
Однородные тригонометрические уравнения.
Определение:1) Уравнение вида a sinx +b cosx=0, (а=0, в=0) называется однородным уравнением первой степени относительно sin x и cos x.
Решается данное уравнение с помощью деления обеих его частей на cos x ![]() 0. В результате получается уравнение a tgx+b=0.
0. В результате получается уравнение a tgx+b=0.
2) Уравнение вида a sin2x +b sinx cosx +c cos2x =0 называется однородным уравнением второй степени, где a, b, c какие-либо числа.
Если а=0, то уравнение решаем делением обеих частей на cos2x ![]() 0. В результате получаем уравнение a tg2x+ b tgx+с =0.
0. В результате получаем уравнение a tg2x+ b tgx+с =0.
Замечание: Уравнение вида a sin mx +b cos mx=0 или
a sin2 mx +b sin mx cos mx +c cos2 mx =0 также являются однородными. Для их решения обе части уравнения делят на cos mx=0 или cos2 mx=0
3) К однородным уравнениям могут быть сведены различные уравнения, которые первоначально не являются такими. Например, sin2 mx +b sin mx cos mx +c cos2 mx =d, и a sinx +b cosx=d. Для решения этих уравнений необходимо умножить правую часть на « тригонометрическую единицу» т.е. на sin2x + cos2x и выполнить математические преобразования.
Упражнения на закрепление изученного материала:
1) 2sin x- 3cos x = 0; 5) 4 sin2x – sin2x =3;
2) sin 2x+ cos2x = 0; 6) 3 sin2x + sinx cosx =2 cos2x ;
3) sin x+ 3cos x = 0; 7) 3 sin2x- sinx cosx =2;
4) sin2x -3 sinx cosx +2 cos2x =0
3.Подведение итогов урока . Домашнее задание.
На данном занятии в зависимости от подготовленности группы можно рассмотреть решение уравнений вида a sin mx +b cos mx=с, где а, b,с не равны нулю одновременно.
Упражнения на закрепление:
1. 3sin x + cos x=2;
2. 3sin 2x + cos 2x= 2;
3. sin x/3 + cos x/3=1;
4. 12sin x +5 cos x+13=0.
№ 3 Решение тригонометрических уравнений
Цель: 1) Изучить метод решения тригонометрических уравнений разложением на множители; научиться решать тригонометрические уравнения с использованием различных тригонометрических формул;
2) Проконтролировать: знание учащимися формул для решения простейших тригонометрических уравнений; умение решать простейшие тригонометрические уравнения.
План занятия:
-
Проверка домашнего задания.
-
Математический диктант.
-
Изучение нового материала.
-
Закрепление изученного материала через решение уравнений различной сложности.
-
Самостоятельная работа.
-
Подведение итогов занятия. Домашнее задание.
Ход занятия:
-
Проверка домашнего задания (решение тригонометрических уравнений кратко записаны на доске).
-
Математический диктант.
В-1
1. Какие уравнения называются простейшими тригонометрическими уравнениями?
2. Как называется уравнение вида a sinx +b cosx=0? Укажите способ его решения.
3.Запишите формулу корней уравнения tgx = a (ctg x=a).
4. Запишите формулы корней уравнений вида cosx=a, где а=1, а=0, а=-1.
5. Запишите общую формулу корней уравнения sin x=a, |a|
6. Как решаются уравнения вида acosx=b, |b|
В-2
1. Запишите формулы корней уравнений cosx=a,|a|
2. Запишите общую формулу корней уравнения
=a, |a|
3. Как называются уравнения вида sin x=a, tgx = a, sin x=a?
4.Запишите формулы корней уравнения sin x=a, если а=1, а=0, а=-1.
5.Как решаются уравнения вида sin ax=b, |b|
6. Какие уравнения называются однородными уравнениями второй степени? Как они решаются?
-
Изучение нового материала.
Метод разложения на множители.
Одним из наиболее употребительных методов решения тригонометрических уравнений является метод разложения на множители.
Если уравнение f(x) =0 можно представить в виде f1(x) f2(x) =0 , то задача сводится к решению двух уравнений f1(x)=0, f2(x) =0.
( С учащимися полезно вспомнить правило «Произведение множителей равно нулю, если хотя бы один из множителей равен нулю, а другие при этом имеют смысл»)
-
Закрепление изученного материала через решение уравнений различной сложности.
-
(sin x-1/2)( sin x+1)=0; 2) (cosx- 2/2)( sin x+ 2/2)=0;(самост.)
3) sin2 x+ sin x cosx=0; 4) sin2 x- sin x =0;
5 ) sin 2x – cosx=0; 6) 4 cos2x -1 =0; (2-мя способами)
7) cosx+ cos3x=0; 8) sin 3x= sin 17x;
9) sin x+ sin 2x+ sin 3x=0; 10) cos3x cos5x
11) sin x cos5x =sin 9x cos3x sin 2x sin 2x
12) 3 cosx sin x+ cos 2x=0(самост.)
13) 2 cos2x - sin (x- ![]() /2)+ tgx tg (x+
/2)+ tgx tg (x+![]() /2)=0.
/2)=0.
-
Самостоятельная работа.
Вариант-1 Вариант-2
1) 6sin2 x+ 5sin x -1=0; 1) 3 cos 2x+2 cosx -5=0;
2) sin 2x – cos2x=0; 2) 3 cos x/2 - sin x/2=0;
3) 5sin2 x+ sin x cosx -2 cos2 х=2; 3) 4sin2 x- sin x cosx +7cos2 х=5;
4) sin x+sin5x=sin3x+sin7x; 4) sin x-sin 2x +sin 3x-sin 4x=0;
5) sin x+cosx=1. 5) sin x+cosx=2.
8. Подведение итогов урока. Домашнее задание.
Здесь представлен конспект к уроку на тему «Тригонометрические уравнения», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

