Конспект урока «Решение алгебраических уравнений» по алгебре
Тема: Решение алгебраических уравнений.
Цели урока:
-
систематизировать, обобщить, расширить знания и умения учащихся, связанные с применением методов решения алгебраических уравнений;
-
содействовать развитию математического мышления учащихся;
-
побуждать учащихся к преодолению трудностей в процессе умственной деятельности.
План урока.
-
Организационный момент.
-
Доведение цели урока до сознания учащихся.
-
Решение тренировочных упражнений.
-
Самостоятельная работа(выполнение тестового задания, использовалась локальная сеть)
-
Историческая справка.
-
Работа в сети Интернет.
-
Практическая работа по итогам поиска.
-
Подведение итогов урока.
-
Домашнее задание.
-
Организационный момент.
-
Доведение цели урока до сознания учащихся.
Цель урока – закрепить алгоритм решения алгебраических уравнений, рассмотреть различные приемы и методы решения таких уравнений.
Мне бы очень хотелось, чтобы каждый ученик, приходя на урок, считал своей основной задачей: понять объяснения учителя и применить их к решению задач.
-
Решение тренировочных упражнений.
Начнем работу с уравнения, содержащегося в сборнике заданий для проведения экзаменационной работы в 9 классе. Указано, что эти уравнения высокого уровня сложности.
№1. Решите уравнение:
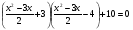
Пусть 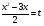 , тогда:
, тогда:
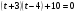
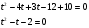
По теореме, обратной теореме Виета:
t1 +t2 = 1 t1 ∙ t2 = -2 │ t1 = 2
2 – 1 = 1 2 ∙ (-1) = -2 │ t2 = - 1
t2 = - 1
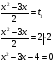
D = b2 -4ac = 9 + 16 = 25, D 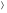 0
0
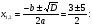
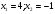
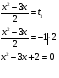
D = b2 - 4ac = 9 - 8 = 1, D 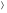 0
0
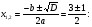
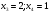
Ответ: -1; 1; 2; 4.
Итак, уравнение решено методом введения новой переменной.
-
. Практическая часть урока.
Далее нам предстоит напряженный этап урока – решить сложное уравнение и выполнить тест (см. приложение).
№ 2. Найти действительные корни уравнения:
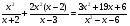
Разложим на множители квадратный трехчлен: 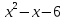 .
.
х2 – х – 6 = 0
По теореме, обратной теореме Виета:
х1+х2 = 1 х1∙ х2 = -6 │ х1 = 3
3 – 2 = 1 3∙ (-2) = -6 │ х2 = -2
Получаем разложение: х2 – х – 6 = (х + 2)(х – 3)
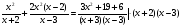
ОДЗ х ≠ 3
х ≠ -2
х2(х-3) + 2х2(х-2)(х+2) = 3х2 +19х + 6
х3 – 3х2+2х2(х2 – 4) = 3х2 + 19х + 6
х3 – 3х2+2х4 – 8х2 – 3х2 – 19х – 6 = 0
2х4 + х3 – 14х2 – 19х – 6 = 0. Ищем корень уравнения среди делителей свободного члена: ± 1; ± 2; ± 3; ± 6
х1 = -1, так как 2 – 1 – 14 +19 – 6 = 0
21 – 21 = 0
2х4+ х3 – 14х2 – 19х – 6 │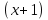
2х4+ 2х3 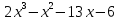
- х3 – 14х2
- х3 – х2
- 13х2 – 19х
- 13х2 – 13х
- 6х – 6
- 6х – 6
0
2х3 – х2 – 13х – 6 = 0. Ищем корень уравнения среди делителей свободного члена: ± 1; ± 2; ± 3; ± 6
х2 = - 2, так как - 16 – 4 + 26 – 6 = 0
- 26 + 26 = 0
2х3 – х2 – 13х – 6│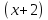
2х3 + 4х2 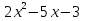
- 5х2 – 13х
- 5х2 – 10х
- 3х – 6
- 3х – 6
0
2х2 – 5х – 3 = 0
D = b2 – 4ac = 25 +24 = 49, D 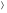 0
0
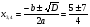 ;
;
х3 = 3 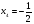
х = 3 – посторонний корень
х = - 2 – посторонний корень
Ответ: - 1; 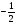
-
Историческая справка.
При решении уравнения использовался прием отыскания действительных корней алгебраического уравнения среди делителей свободного члена. Однако на практике такой прием не всегда позволяет установить корень уравнения.
Долгое время ученые пытались найти формулу корней уравнения третьей степени.
Дело в том, что формула корней квадратного уравнения была изложена еще в III веке греческим ученым Диафантом. Эта формула позволяет найти корень квадратного уравнения, выполнив действия +, -, ∙,: и √(извлечение корня) над коэффициентами уравнения. А так как знак √ - радикал, то говорят, что квадратное уравнение решено в радикалах.
Задача решения в радикалах уравнения третьей степени была решена только в XVI веке. Формулу корней уравнения третьей степени впервые опубликовал итальянский ученый Кардано в 1545 году. К сожалению, наш учебник только упоминает формулу Кардано, а запись формулы не приводит. Попытаемся найти формулу Кардано в Интернете.
-
Работа в сети Интернет.
Поиск формулы Кардано.
-
Практическая работа по итогам поиска.
Итак, мы рассматриваем формулу Кардано для уравнения вида
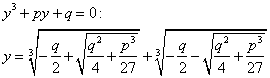
Решим уравнение с помощью формулы Кардано.
y3 – 3y + 2 = 0 (p = - 3; q = 2)
По формуле Кардано:
y1 = 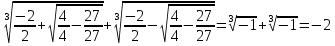
y3 – 3y + 2│(y+2)
y3 + 2y2 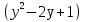
- 2y2 – 3y
- 2y2 – 4y
y + 2
y + 2
0
y2 – 2y+ 1 = 0
(y – 1)2 = 0
y2 = 1 Ответ: - 2; 1.
-
Подведение итогов урока.
Опубликовав свою формулу, Кардано доказал, что уравнение третьей степени разрешимо в радикалах.
Еще 300 лет ученые будут пытаться решить в радикалах уравнения более высоких степеней. Только в 1826 году норвежец Абель докажет, что эти уравнения в радикалах не разрешимы.
-
Домашнее задание.
Найти в Интернете историю открытия формулы Кардано.
Тест
I вариант
№1 Найдите корни квадратного уравнения х2 – 7х – 8 = 0
1) х1 = - 8 2) х1 = 8 3) х1 = - 1 4) х1 = 1
х2 = 1 х2 = - 1 х2 = - 8 х2 = 8
Номер верного ответа:
№2 Числа х1 = 1 и х2 = 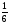 - корни квадратного трехчлена 6х2 – 7х + 1. Разложите квадратный трехчлен на множители.
- корни квадратного трехчлена 6х2 – 7х + 1. Разложите квадратный трехчлен на множители.
-
6х2 – 7х + 1 = (х – 1) (х -
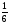 )
) -
6х2 – 7х + 1 = (х + 1) (х +
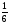 )
) -
6х2 – 7х + 1 = (х – 1) (6х – 1)
-
6х2 – 7х + 1 =6 (х + 1) (х +
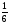 )
)
Номер верного ответа:
№3 Укажите корень уравнения 2х4 + х3 – 14х2 – 19х – 6 = 0.
1) 5 2) – 1 3) – 4 4) 1
Номер верного ответа:
№4 Решите систему уравнений 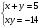
1) (- 7; 2) 2) (7; 2) 3) (7; - 2) 4) (- 7; - 2)
(2; - 7) (2; 7) (- 2; 7) (- 2; - 7)
Номер верного ответа:
№5 Решите систему уравнений 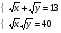
1) (8; 5) 2) (64; 25) 3) (- 8; 5) 4) (64; - 25)
(5; 8) (25; 64) (5; - 8) (-25; 64)
Номер верного ответа:
Ваша оценка:
Тест
II вариант
№1 Найдите корни квадратного уравнения х2 + 2х – 15 = 0
1) х1 = - 5 2) х1 = -3 3) х1 = - 5 4) х1 = 3
х2 = 3 х2 = 5 х2 = - 3 х2 = - 5
Номер верного ответа:
№2 Числа х1 = - 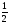 и х2 =
и х2 = 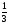 - корни квадратного трехчлена 6х2 + х - 1. Разложите квадратный трехчлен на множители.
- корни квадратного трехчлена 6х2 + х - 1. Разложите квадратный трехчлен на множители.
-
6х2 + х – 1 = (х +
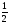 ) (х -
) (х - 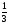 )
) -
6х2 + х – 1 = 6 (х -
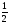 ) (х +
) (х +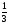 )
) -
6х2 + х – 1 = (2х + 1) (3х – 1)
-
6х2 + х – 1 = (х -
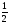 ) (х +
) (х + 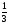 )
)
Номер верного ответа:
№3 Укажите корень уравнения 2х4 - 3 х3 – 7х2 – 5х – 3 = 0.
1) 5 2) – 1 3) – 4 4) 1
Номер верного ответа:
№4 Решите систему уравнений 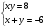
1) (- 4; 2) 2) (4; 2) 3) (4; - 2) 4) (- 4; - 2)
(2; - 4) (2; 4) (- 2; 4) (- 2; - 4)
Номер верного ответа:
№5 Решите систему уравнений 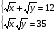
1) (7; 5) 2) (49; 25) 3) (- 7; - 5) 4) (- 49; - 25)
(5; 7) (25; 49) (- 5; - 7) (-25; - 49)
Номер верного ответа:
Ваша оценка:
©BocharovaEV,2011
Здесь представлен конспект к уроку на тему «Решение алгебраических уравнений», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

