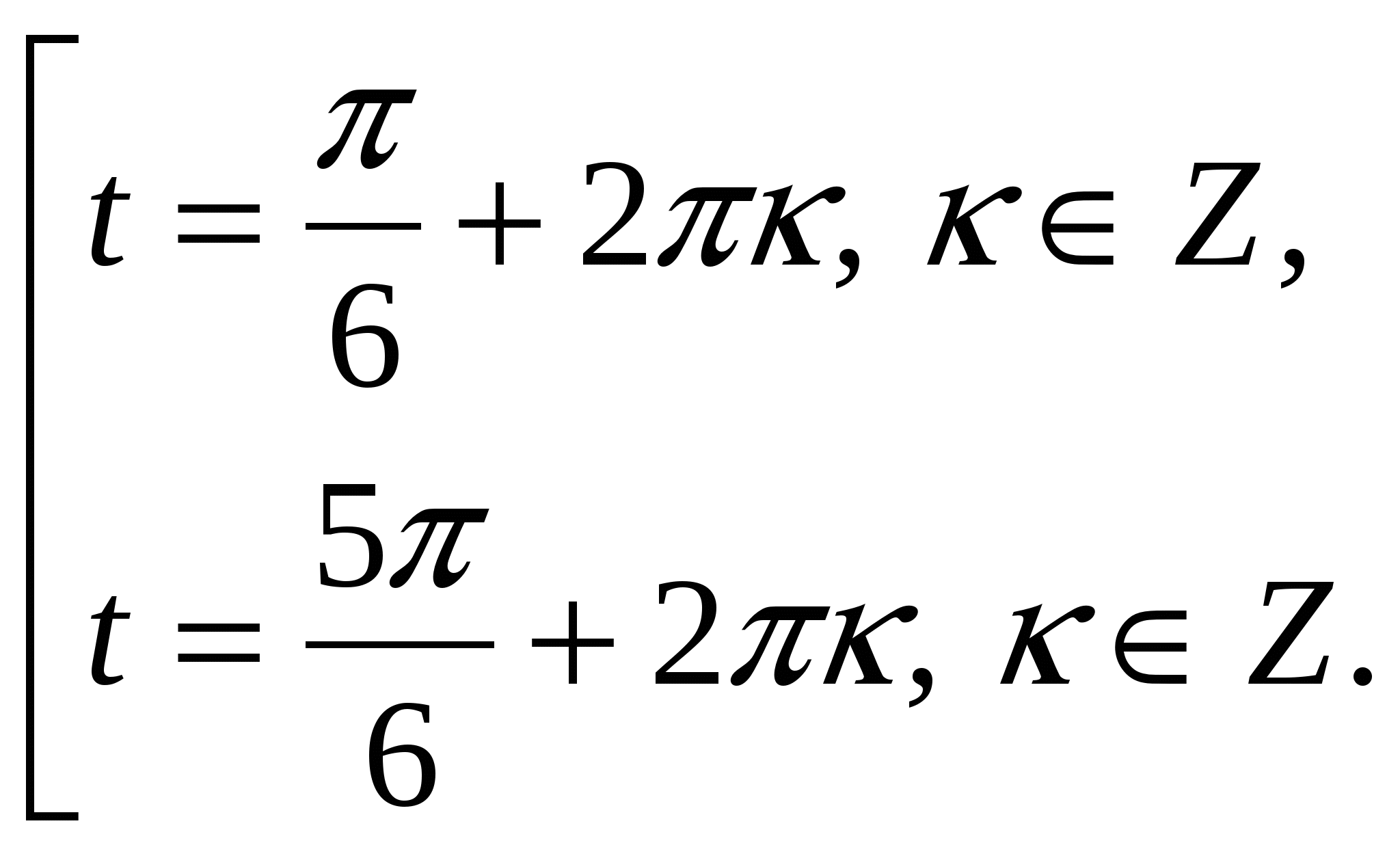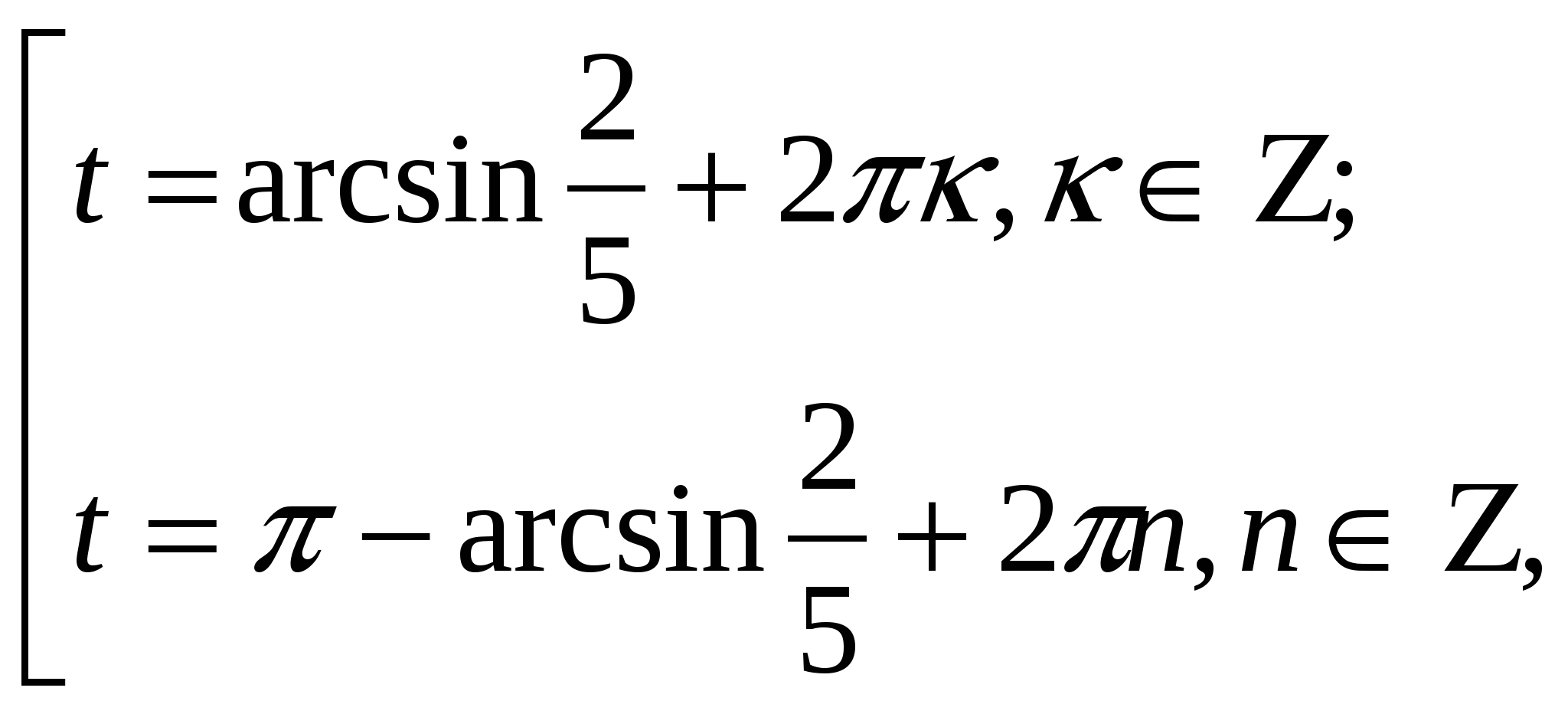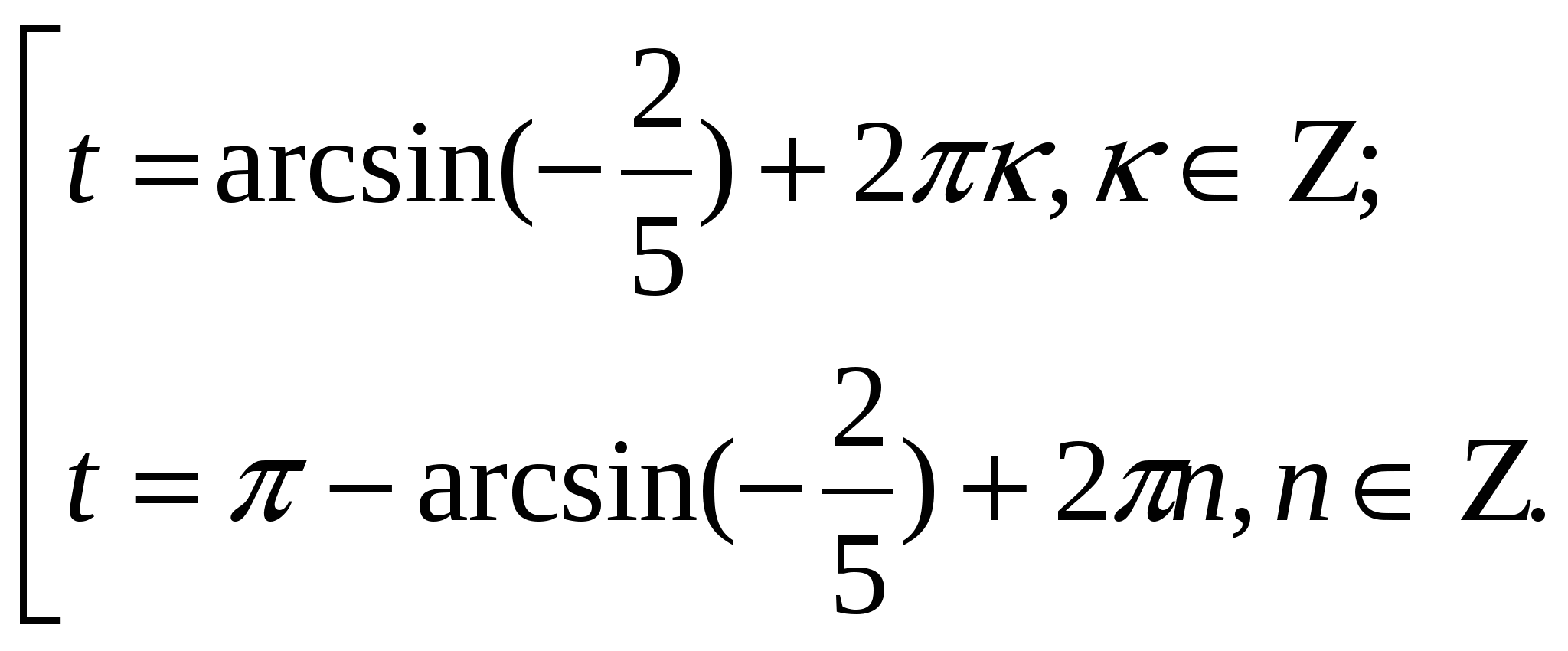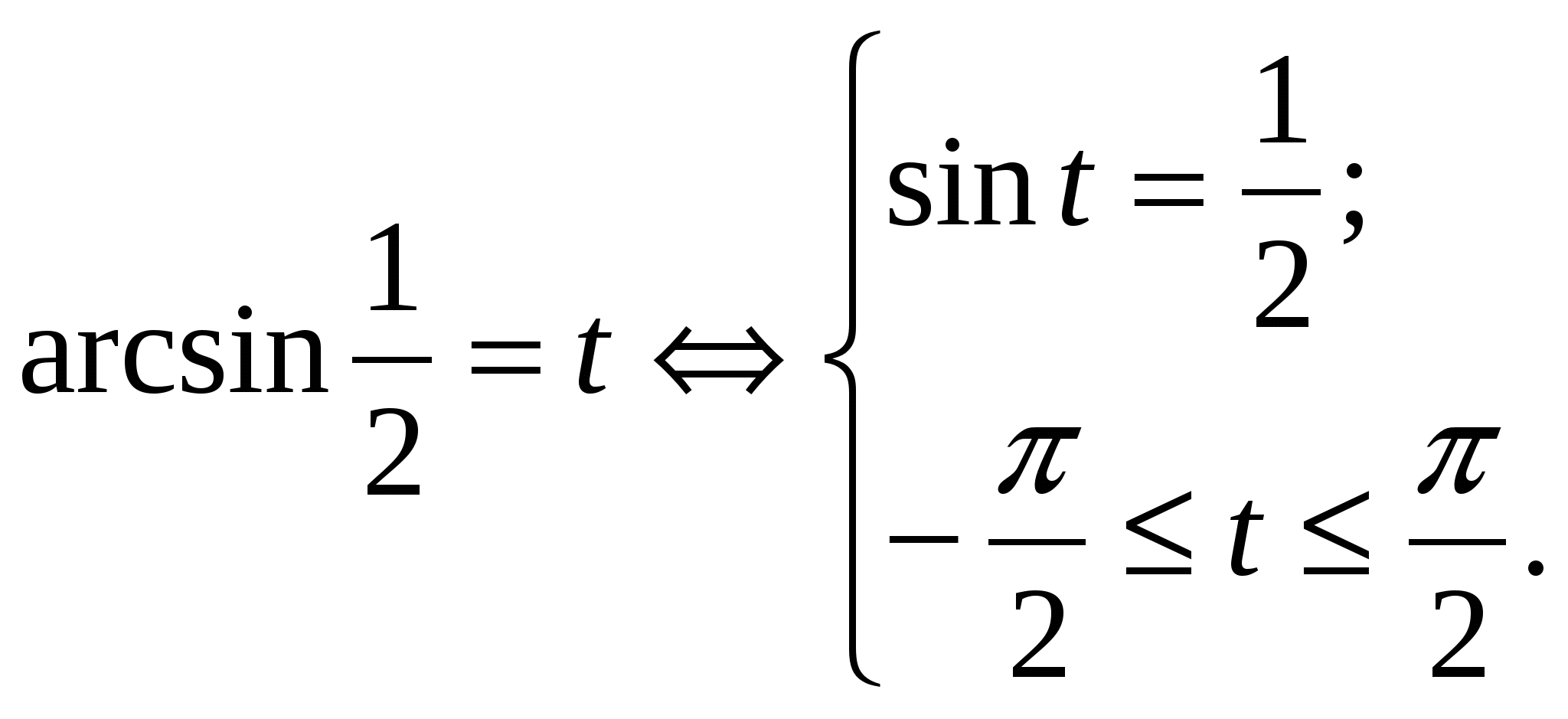Конспект урока «Арксинус. Решение уравнения sin t =a» по алгебре для 10 класса

Этапы урока и их содержание

Время (мин)

Деятельность

учителя

учащегося

I

Организационный этап.

1

Организационная.

Сообщают об отсутствующих.

II

Постановка целей.

Сегодня на уроке мы введем понятие арксинуса; выведем общую формулу решения уравнения sin t = a; выработаем алгоритм решения данного уравнения.

1

Сообщает тему урока, дату проведения урока, цель урока.

Открыли рабочие тетради и записали тему урока.

III

Домашнее задание.

Изучить теоретический материал.

Практическая часть (даётся задание в соответствии с используемым учебным пособием).

1

Комментирует домашнее задание.

Получают задание.

IX

Актуализация опорных знаний (устная работа).

Повторить способ решения уравнения вида

sin t = a, где а – действительное число, с помощью числовой окружности.

Решить уравнения: sin t = .

Используем геометрическую модель – числовую окружность на координатной плоскости.

sin t = ;

5

Показывает презентацию.

Слайд №2

Слайд №3

Задает вопросы.

Отвечают на вопросы.

V

Изучение нового материала.

Ввести проблемную ситуацию: любое ли тригонометрическое уравнение вида

sint = a можно решить с помощью числовой окружности?

1) Предложить учащимся решить уравнение

sin t = .

С помощью числовой окружности получим

t₁ и t₂.

Когда впервые возникла ситуация с решение уравнений такого типа, ученым-математикам пришлось придумать способ её описания на математическом языке. В рассмотрение был введен новый символ

arcsin а.

Читается: арксинус а; «arcus» в переводе с латинского значит «дуга» (сравните со словом «арка»). С помощью этого символа числа t₁ и t₂ записываются следующим образом:

t₁ = arcsin , t₂ = – arcsin .

Теперь с помощью этого символа корни уравнения sin t = можно записать так:

Предложить учащимся обобщить полученные знания, ответив на вопрос: «Что же означает arcsin ?»

Вывод: это число (длина дуги), синус которого равен и которое принадлежит первой четверти числовой окружности.

2) Решить уравнение sin t = – .

С помощью числовой окружности и символа arcsin а получим:

Предложить учащимся обобщить полученные знания, ответив на вопрос: «Что же означает arcsin () ?»

Вывод: это число (длина дуги), синус которого равен и которое принадлежит четвёртой четверти числовой окружности.

3) Сформулировать определение арксинуса в общем виде.

4) Рассмотреть примеры на вычисление арксинуса.

Пример 1. Вычислите arcsin.

Решение.

Пусть

Значит, поскольку и Итак, arcsin=

Пример 2. Вычислите arcsin.

Пример 3. Вычислите arcsin 0.

5) Доказать теорему и рассмотреть её применение на практике.

Теорема.

Для любого а [-1;1] выполняется равенство arcsin a + arcsin (-a) =0.

Применение теоремы.

На практике используется:

arcsin (-a) = - arcsin a , где 0 ≤ а ≤ 1.

Пример.

arcsin= - arcsin = -

6) Сделать общий вывод о решении уравнения sin t = a .

Если │a│≤ 1, то уравнение sint = a имеет решения: .

7) Рассмотреть частные случи.

Выделим формулы для решения следующих уравнений: sin t = 0, sin t =1 , sin t = –1.

26

Слайд №4

Формулирует задание, показывает решение обсуждая каждое действие с учащимися.

Слайд №5

Слайд №6

Слайд №7

Формулирует вопрос.

Слайд №8

Показывает решение уравнения обсуждая каждое действие с учащимися.

Слайд №9

Формулирует вопрос.

Слайд №10

Слайд №11

Показывает решение обсуждая каждое действие с учащимися.

Слайд №12

Показывает решение

Слайд №13

Показывает решение.

Слайд №14

Доказывает теорему.

Слайд №15

Показывает применение теоремы на практике.

Слайд №16-17

Слайд №18

Отвечают на вопрос.

Работают в форме диалога с учителем, оформляют решение в тетради

Выполняют записи в тетради.

Записывают определение.

Работают в форме диалога с учителем, оформляют решение в тетради.

Записывают определение.

Записывают определение.

Работают в форме диалога с учителем, оформляют решение в тетради.

Один из учеников комментирует решение, остальные проверяют своё решение.

Выполняют записи в тетради.

Выполняют записи в тетради.

Выполняют записи в тетради.

Выполняют записи в тетради.

VI

Обобщение изученного материала.

Составим алгоритм решения простейшего тригонометрического уравнения вида sin t = a:

• составить общую формулу;

• вычислить значение arcsin a;

• подставить найденное значение в общую формулу.

Пример 1. Решить уравнение sin t = .

Пример 2. Решить уравнение sin t = .

Пример 3. Решить уравнение sin t = .

Пример 4. Решить уравнение sin t = - 1,2.

10

Показывает решение уравнений на примерах.

Слайд №19

Слайд №20-21

Слайд №22

Слайд №23

Работают в форме диалога с учителем, оформляют решение в тетради.

VII

Итоги урока.

Итак, сегодня на уроке мы ввели понятие арксинуса; вывели общую формулу решения уравнения sin t = a и выработали алгоритм решения данного уравнения.

Спасибо за урок!

1

Слайд №24