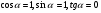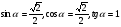Конспект урока «Синус, косинус и тангенс угла» по алгебре для 9 класса
Разработка урока в 9 классе «Синус, косинус, и тангенс угла».
Предмет: Геометрия.
Класс:9 класс.
Авторы учебника: Атанасян Л.С., Бутузов В.Ф. и другие Геометрия 7-9: Издательство «Просвещение», 2013.
Цели урока:
-
Ввести понятие синуса, косинуса и тангенса для углов от 00до 1800.
-
Вывести основное тригонометрическое тождество и формулы для вычисления координат точки.
-
Рассмотреть формулы приведения.
-
Формирование мыслительных операций (анализ, синтез, сравнение, абстрагирование).
-
Способствовать саморазвитию учащихся путём постановки целей и достижения результатов учебной деятельности.
Ход урока:
| Время (мин) | Действия учителя | Действия учеников | Описание презентации | |
| 1,2 | 1с | Учитель приветствует учеников, сообщает тему урока, ставит цель урока. | Слушают учителя. Записывают тему урока. | По щелчку: Синус, косинус и тангенс угла. |
| 3 | 2 | Повторение опорных знаний. Предлагает ученикам повторить соотношения в прямоугольном треугольнике, используя для наглядности слайд. | Ученики записывают соотношения в тетрадь. | Заголовок: Синус, косинус и тангенс в прямоугольном треугольнике. Треугольник АВС
По щелчку: Изменяют цвет прямые АС, АВ на синий.
По щелчку: Изменяют цвет прямые АС, ВС на зелёный. |
| 4 | 2 | Учитель предлагает ребята пройти тест с последующей Самопроверкой с целью повторения соотношений между сторонами и углами в прямоугольном треугольнике. | В тетрадях решают тест. По завершении работы обмениваются тетрадями, проверяют друг у друга. Правильные ответы показаны на экране. | Заголовок: Проверь себя Тест с вариантами ответов По щелчку: поочерёдно вылетают прямоугольники, указывающие на правильный ответ. |
| 5 | 5 | Изучение нового материала. Введём прямоугольную систему координат Оху и построим полуокружность радиуса 1 с центром в начале координат, расположенную в первом и втором квадрантах. Назовём её единичной полуокружностью. Из точки О проведём луч, пересекающий единичную полуокружность в точке М(х;у). Обозначим Если α- острый , то из ∆ОММ1 имеем:
| Делают чертёж, записывают вывод формул. | Заголовок: Синус, косинус и тангенс угла Чертёж единичной полуокружности в прямоугольной системе координат. По щелчку: поочерёдно вылетают объекты: линия, М, α,М1,линия, х, у. По щелчку: данные объекты исчезают и появляются уже во 2 четверти (угол - тупой) По щелчку: По щелчку:
По щелчку:
|
| 6 | 3 | На слайде изображены система координат Оху и единичная полуокружность. Эта полуокружность является дугой окружности, заданной уравнением:
Подставляя выражения для х и у имеем:
Это равенство называется основным тригонометрическим тождеством. Следствием его являются формулы:
| Чертёж используют предыдущий. Записывают вывод тождества, формулы. | Заголовок: Основное тригонометрическое тождество
По щелчку:
По щелчку: По щелчку:
|
| 7 | 5 | Справедливы следующие тождества. Они называются формулами приведения.
Составим таблицу для значений синуса, косинуса, тангенса углов: 00,900, 1800. Значения 300,450, 600 нам уже знакомы. Значения синуса, косинуса и тангенса 1200, 1350,1500 заполним, используя формулы приведения. | Записывают формулы приведения, чертят таблицу. Для вычисления значений синуса, косинуса и тангенса 1200, 1350,1500 приглашаются ученики к доске. | Заголовок: Формулы приведения По щелчку:
По щелчку: таблица По щелчку: поочерёдно значения функций для заданных углов |
| 8 | 3 |
| Записывают формулы. | Заголовок: Координаты точки. Чертёж единичной полуокружности.
По щелчку: |
| 9 | 5 | Формирование знаний, умений. Учитель предлагает вычислить ученикам синус, косинус, тангенс угла: А) АОМ Б) АОС В) АОК Г) АОВ | По вариантам: 1 вариант: а и в 2 вариант: б и г. Проводят взаимопроверку. | Заголовок: Найти синус, косинус, тангенс угла: По щелчку: А) АОМ Б) АОС В) АОК Г) АОВ
По щелчку:
По щелчку:
По щелчку:
|
| 10 | 2 | Учитель объясняет решение задачи: Принадлежит ли единичной полуокружности точка: Р(-0,6;0,8) решение:
| Ученики записывают решение задачи в тетрадь. | Заголовок: Принадлежит ли единичной полуокружности точка: Р(-0,6;0,8)
|
| 11 | 2 |
| Заголовок: Найти синус и тангенс угла
По щелчку:
| |
| 8 | Самостоятельно решите задачи: № 1012, 1013, 1015(а,б) | Решают самостоятельно. Проверяем ответы: №1012 М1(0;1) лежит на единичной полуокружности. М2,М3,М4 лежат на единичной полуокружности Проговаривают значения синуса, косинуса и тангенса для каждой точки. 31013 А) №1015 А) Б) | ||
| 2 | Итог урока. Учитель объявляет оценки. Домашнее задание: п.п.93-95, вопросы 1-6, №1011,1014,1015(б,г) | |||
Здесь представлен конспект к уроку на тему «Синус, косинус и тангенс угла», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (9 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

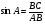 По щелчку:
По щелчку: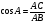 Изменяют цвет объект А, прямые ВС. ,АВ на красный.
Изменяют цвет объект А, прямые ВС. ,АВ на красный.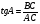
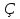 угол между лучом Ом и положительной полуосью абсцисс.
угол между лучом Ом и положительной полуосью абсцисс.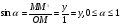
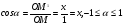
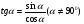 . Итак, синус острого угла равен ординате у точки М, а косинус угла α- абсциссе точки М. Если угол α прямой, тупой или развёрнутый или α=00, то синус, косинус угла α также определяем по данным формулам. Т.О., для любого угла α из промежутка от 00 до 1800 синусом угла α называется ордината у точки М, а косинусом угла α- абсцисса точки М.
. Итак, синус острого угла равен ординате у точки М, а косинус угла α- абсциссе точки М. Если угол α прямой, тупой или развёрнутый или α=00, то синус, косинус угла α также определяем по данным формулам. Т.О., для любого угла α из промежутка от 00 до 1800 синусом угла α называется ордината у точки М, а косинусом угла α- абсцисса точки М.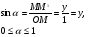

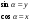 По щелчку:
По щелчку: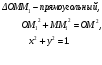 Х2+у2=1.
Х2+у2=1.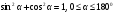
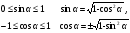
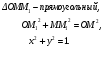 Чертёж единичной полуокружности.
Чертёж единичной полуокружности.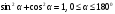
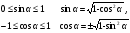
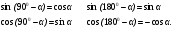
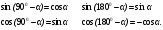
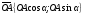
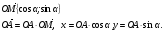 Пусть задана система координат Оху и дана произвольная точка А (х; у). Выразим координаты точки А через длину отрезка ОА и угол α между лучом ОА и положительной полуосью Ох. Обозначим буквой М точку пересечения луча ОА с единичной полуокружностью. Вектор
Пусть задана система координат Оху и дана произвольная точка А (х; у). Выразим координаты точки А через длину отрезка ОА и угол α между лучом ОА и положительной полуосью Ох. Обозначим буквой М точку пересечения луча ОА с единичной полуокружностью. Вектор 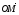 имеет те же координаты, что и точка М, т.е.
имеет те же координаты, что и точка М, т.е.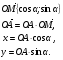 По щелчку:
По щелчку: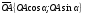
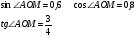 По щелчку:
По щелчку: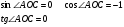
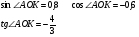
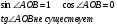
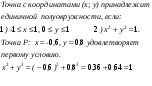
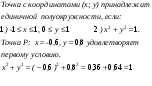 По щелчку:
По щелчку: 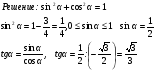
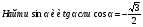
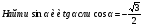 По щелчку:
По щелчку:
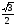 б)
б) 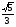 в) 0
в) 0