Конспект урока «РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ» по алгебре для 10 класса
Автор : Чирясова Наталия Константиновна
Место работы: ГОУ СОШ № 935, г. Москва.
Должность: учитель математики.
Дополнительные сведения: урок алгебры и начал
анализа по теме: « Решение тригонометрических
уравнений» для 10 класса.
Урок алгебры и начал анализа в 10 классе.
Тема: «РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ»
Тип урока : урок обобщения и систематизации знаний.
Цель урока: закрепить навыки решения тригонометрических уравнений различных типов.
Задачи урока.
1. Образовательные:
- закрепление программных знаний и умений по решению тригонометрических уравнений;
- обобщение и систематизация материала;
- создание условий для контроля и самоконтроля усвоения знаний и умений;
- установление межпредметных связей.
2. Воспитательные:
- воспитание навыков делового общения, активности;
-формирование интереса к математике и ее приложениям.
3. Развивающие:
- формирование умений применять приемы: сравнения, обобщения, выделения главного, переноса знаний в новую ситуацию,
- развитие познавательного интереса, математического кругозора, мышления и речи, внимания и памяти.
Формы организации работы учащихся на уроке:
индивидуальная, фронтальная, парная.
Методы обучения:
частично-поисковый (эвристический), тестовая проверка уровня знаний, работа по опорным схемам, работа по обобщающей схеме, решение познавательных обобщающих задач, системные обобщения, самопроверка, взаимопроверка.
Оборудование и источники информации: таблицы (плакаты) по теме «Решение тригонометрических уравнений», системно-обобщающая схема (приложение 1);
на партах учащихся: опорные схемы по решению тригонометрических уравнений, листы учета знаний, лист бумаги для проведения теста и копирка.
1. Организационный момент.
Эпиграф занятия: «Без уравнения нет математики как средства познания природы» (академик Александров П. С.).
Учитель: «Сегодня у нас заключительный урок по теме «Решение тригонометрических уравнений». Повторяем, обобщаем, приводим в систему изученные виды, типы, методы и приемы решения тригонометрических уравнений.
Перед вами стоит задача – показать свои знания и умения по решению тригонометрических уравнений. Все виды работ на уроке будут оценены, результаты занесены в лист учета знаний».
2. Повторение теории.
Вопросы к классу:
1). Какое уравнение называется тригонометрическим?
2). Каков алгоритм решения тригонометрических уравнений?
3).Уравнения какого вида называются простейшими тригонометрическими уравнениям?
Учитель: «Рассмотрим решение простейших тригонометрических уравнений, повторим основные формулы». Ученики работают с опорным конспектом (приложение №1).
3. Выполнение теста.
Работа выполняется на листах бумаги с копиркой.
| Вариант 2 | |
| 1) Каково будет решение уравнения | 1) Каково будет решение уравнения |
| 2) При каком значении | 2) При каком значении |
| 3) Какому промежутку принадлежат значения | 3) Какому промежутку принадлежат значения |
| 4) Какой формулой выражается решение уравнения | 4) Какой формулой выражается решение уравнения |
| 5) Каким будет решение уравнения | 5) Каким будет решение уравнения |
| 6) Чему равен | 6) Чему равен |
| 7) Какой формулой выражается решение уравнения | 7) Какой формулой выражается решение уравнения |
Ученики сдают первый экземпляр работы, по второму экземпляру осуществляется контроль в ходе самопроверки (правильные ответы записываются на обратной стороне доски). Результаты заносятся в лист учета знаний.
Выполняется работа над ошибками.
4. Устная работа.
Учитель: «Исправьте ошибки на доске и подумайте об их причинах».
| Ответ с ошибкой | Правильный ответ | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Нет корней |
|
|
|
|
5. Работа в группах.
Математическая эстафета «Вертушка».
Каждая группа получает набор из 6 карточек с уравнением. Решив уравнение, ученик передает карточку своему соседу. Карточки проходят по кругу, поэтому эстафета называется « Вертушка».
| Ответы | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проводится взаимопроверка работ. Группы обмениваются тетрадями.
Результаты записываются в лист учета знаний ученика в баллах (по одному баллу за каждое задание).
6. Историческая справка о развития тригонометрии, решении тригоно- метрических уравнений
Выступление ученика.
7. Решение прикладной задачи
Учитель: «Решение прикладных задач помогает формировать представление о роли математики в изучении окружающего мира, видеть разницу между реальным и идеальным, между физическим явлением и его математической моделью.
О прикладной направленности изучаемой темы расскажет ученик, который подготовил физическую задачу».
Задача. Под каким углом ![]() должен плыть пловец, чтобы из точки А попасть в точку
должен плыть пловец, чтобы из точки А попасть в точку ![]() , если скорость пловца
, если скорость пловца ![]() , скорость течения реки
, скорость течения реки ![]() ,
, ![]() ? (см. рис к задаче).
? (см. рис к задаче).
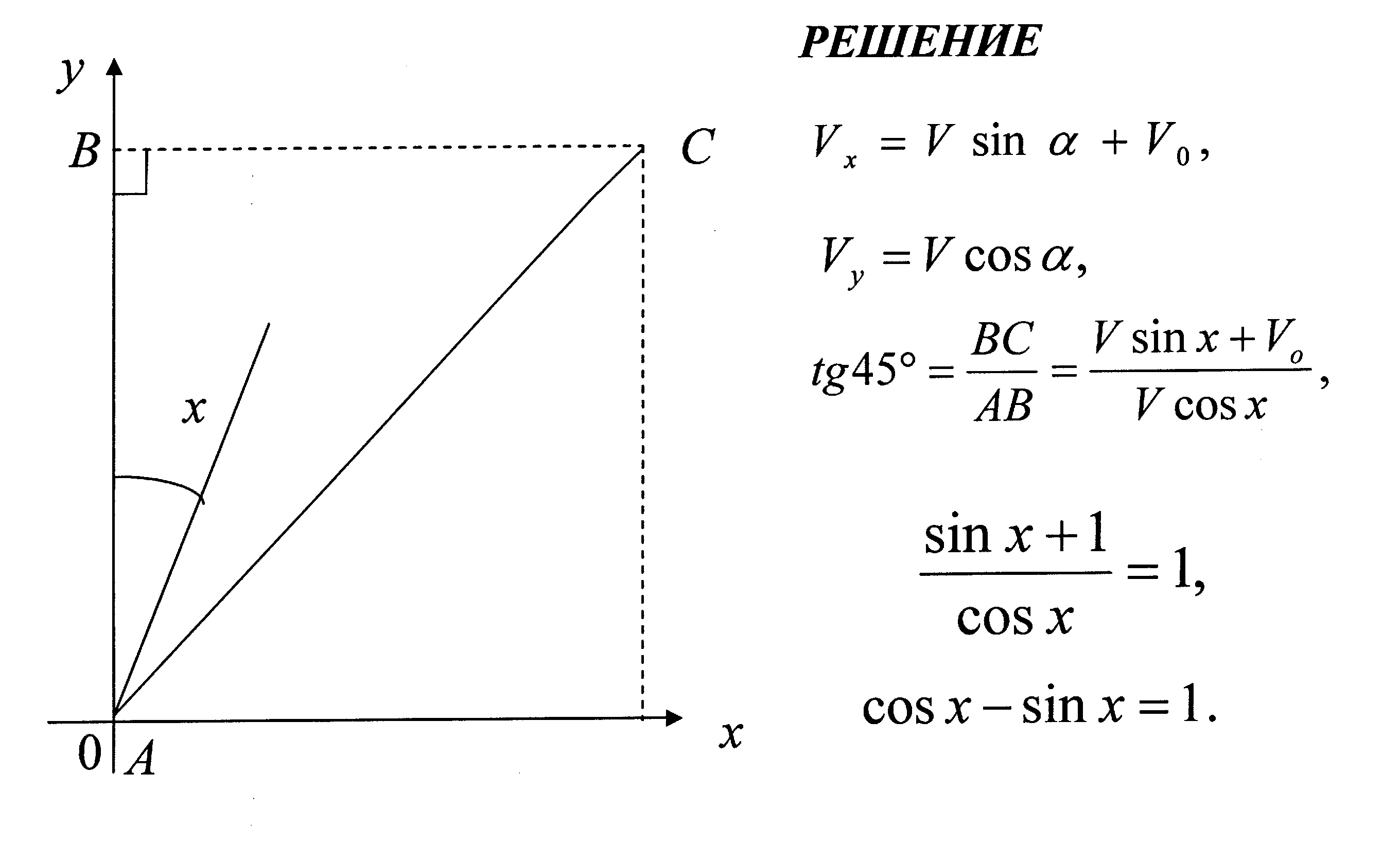
Решение Vx=V sin x + V0, Vy=V cos x, tg 45º= cos x – sin x=1.![]() =
=![]() ,
,![]()
![]() =1,
=1,
Ученикам предлагается решить полученное в задаче тригонометрическое уравнение различными способами, работая в группе.
1-я группа решает методом приведения к однородному уравнению.
2-я группа – методом разложения на множители.
3-я группа- методом введения вспомогательного угла.
4-я группа – методом преобразования разности в произведение
Ответы представителей групп:
1 способ. Приведение к однородному уравнению.
cos x – sin x=1,
cos2![]() – sin2
– sin2![]() –2sin
–2sin ![]() cos
cos![]() =sin2
=sin2 ![]() + cos2
+ cos2![]() ,
,
2sin2![]() +2sin
+2sin ![]() cos
cos![]() =0.
=0.
sin![]() ( sin
( sin![]() + cos
+ cos![]() )=0.
)=0.
1) sin![]() =0, 2) sin
=0, 2) sin![]() + cos
+ cos![]() =0,
=0,
![]() =πn, n∈Z. tg
=πn, n∈Z. tg![]() = –1,
= –1,
x=2 πn, n∈Z. ![]() = –
= – ![]() + πn, n∈Z,
+ πn, n∈Z,
x= – ![]() +2 πn, n∈Z.
+2 πn, n∈Z.
![]() 2 способ. 3 способ
2 способ. 3 способ
Разложение Введение
на множители вспомогательного угла
cos x – sin x=1, cos x – sin x=1,
(cos x – 1) - sin x = 0, ![]() (cos x
(cos x![]() – sin x
– sin x![]() )=1,
)=1,
(1- cos x) + sin x = 0, sin![]() cos x – cos
cos x – cos![]() sin x=1,
sin x=1,
2sin2![]() + 2sin
+ 2sin ![]() cos
cos![]() = 0, sin(
= 0, sin(![]() – x)=
– x)= ![]() .
.
sin![]() ( sin
( sin![]() + cos
+ cos![]() ) = 0.
) = 0.
4 способ. Преобразование разности в произведение.
cos x – sin x=1,
sin (![]() - x) - sin x = 1,
- x) - sin x = 1,
2 sin (![]() - x) cos
- x) cos![]() = 1,
= 1,
sin(x - ![]() )= -
)= -![]() ,
,
x = 2 πn, n∈Z;
x = – ![]() +2 πn, n∈Z.
+2 πn, n∈Z.
Учитель: «Решение проведено в общем виде, применительно к реальным явлениям
x =0°».
8. Решение упражнений на систематизацию уравнений.
Ученикам предлагаются блоки уравнений на сравнение, обобщение, выделение главного.
-
Что бы это значило?
| 1) sin x + cos x = 0 |
| 2) sin2 x - 5 sin x cos x + 6 cos2 x = 0 |
| 3) 4 sin x cos x - cos2 x= 0 |
| Можно ?! |
Ответ: 1 - однородное уравнение первой степени, решается методом деления
на cos x (sin x);
2 - однородное уравнение второй степени, решается методом деления
на cos2 x (sin2 x);
3 - нельзя делить на cos2x, это приведет к потере корней.
-
Найти лишнее в этом блоке уравнение и раскрыть идею его решения.
| 2) |
| 3) 8 cos 6x +4 cos x = 0 |
Ответ: 1, 3 - уравнения, решающиеся методом разложения на множители;
2 - лишнее уравнение в этом блоке, содержит обратную
тригонометрическую функцию. Так как x + 1=![]() , x = -
, x = -![]() .
.
| 2) |
| 3) cos x + |
Ответ: 2, 3 -уравнения, решающиеся методом введения вспомогательного угла;
1- лишнее уравнение в этом блоке, оно решается оценкой значений левой и правой части. Так как наибольшее значение левой части равно 6, 6![]() 7, это уравнение корней не имеет.
7, это уравнение корней не имеет.
9. Подведение итогов урока.
Учитель: «Сегодня на уроке мы повторили решение разных типов тригонометрических уравнений, решали уравнения различными методами, рассмотрели задачу по физике, которая решалась с помощью тригонометрического уравнения».
Проводится рефлексия. Лист учета знаний ученики сдают учителю, за работу
на уроке выставляется оценка в журнал.
10. Домашнее задание.
Решение уравнений из материалов ЕГЭ: задание С-1 п.4 №16,17,18; задание С-3 п.6 №3,4,5 из пособия по подготовке к ЕГЭ-2011 под редакцией А. Л. Семенова,
И.В. Ященко)
Список использованных источников:
1. Материалы ЕГЭ под редакцией А. Л. Семенова, И. В. Ященко.
М: МЦНМО, 2011.
2. А. Газизова. Решение тригонометрических уравнений. Газета « Математика», приложение к « 1 Сентября», № 20, 2000.
Приложение № 1. Опорный конспект - системно-обобщающая схема по решению тригонометрических уравнений.

Здесь представлен конспект к уроку на тему «РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (10 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

