Конспект урока «РЕШЕНИЕ СЛОЖНЫХ ЛОГАРИФМИЧЕСКИХ НЕРАВЕНСТВ» по алгебре
РЕШЕНИЕ СЛОЖНЫХ ЛОГАРИФМИЧЕСКИХ НЕРАВЕНСТВ
Цель урока:
-
Сформировать умения учащихся решать сложные логарифмические неравенства, а также неравенства смешанного типа.
-
Не допускать ошибок в проводимых преобразованиях. Следить за тем, чтобы каждое действие не расширяло и не сужало область допустимых значений неравенства, то есть не приводило ни к потере, ни к приобретению посторонних решений.
-
Развитие у учащихся логического мышления . Умение учащихся оперировать такими понятиями, как система неравенств (пересечение множеств), совокупность неравенств (объедение множеств), осуществлять отбор решений неравенства, руководствуясь его областью допустимых значений
-
Освоение всеми учащимися алгоритмов решения сложных логарифмических неравенств, закрепление теоретических знаний при решении конкретных примеров;
-
Развитие культуры научных и учебных взаимоотношений между учениками и между учениками и учителем; воспитание навыков совместного решения задач.
«В науке нет широкой столбовой дороги,
и только тот может достигнуть её сияющих вершин,
кто не страшась усталости,
карабкается по её каменистым тропам.»
К. Маркс
Ход урока
-
Организационный момент (формулировка темы, постановка целей и задач урока перед учащимися, план хода урока)
-
Актуализация опорных знаний проводится в форме беседы по лекционному материалу по данной теме.
-
Понятие сложного логарифмического неравенства
Под сложным логарифмическим неравенством понимают неравенство вида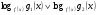 
, где 
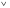– один из знаков неравенств: 
.
-
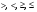Алгоритм решения сложного логарифмического неравенства
Так как при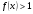 
функция 
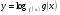является возрастающей, а при – убывающей, то для решения сложного логарифмического неравенства необходимо рассмотреть два случая, т. е. решить совокупность двух систем:
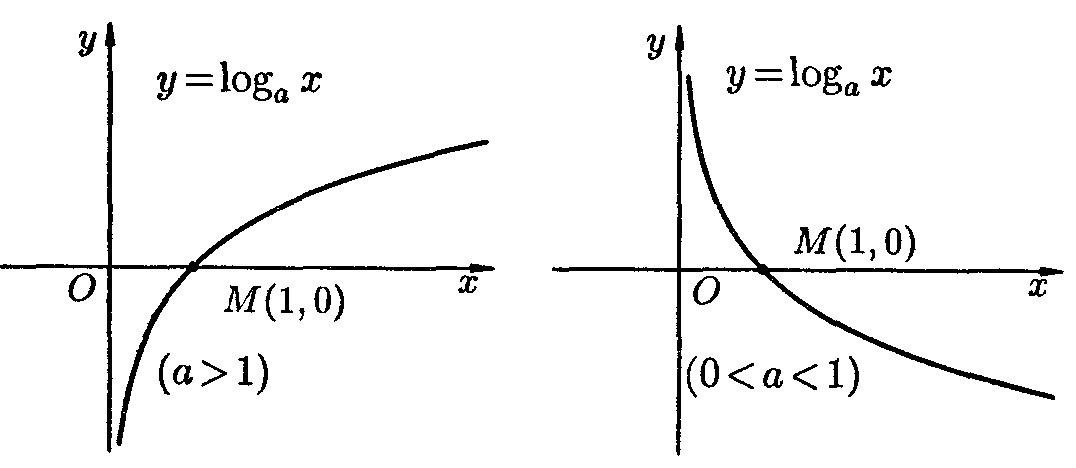
Решение сложных логарифмических неравенств методом эквивалентной замены их одной системой неравенств
Решение сложных логарифмических неравенств совокупностью двух систем можно значительно упростить, применяя эквивалентную замену:
-
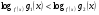
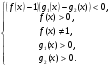
Решение задач:.
Пример 1.
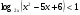
Решается двумя способами(совокупностью двух систем; эквивалентной системой) на доске разными учениками одновременно. Далее проводится обсуждение каждого из методов решения, определяется более рациональный
.Решение:
1 способ
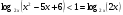
Данное неравенство равносильно совокупности двух систем рациональных неравенств:
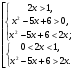
x
6
3
2
1
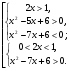
x
6
1
0
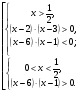
Решение совокупности:
x
6
3
2
1
0
Ответ.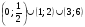 
.
2 способ
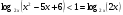
Данное неравенство равносильно системе рациональных неравенств:
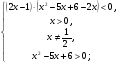
x
6
3
2
1
0
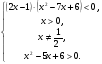
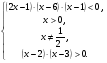
Ответ. .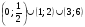
Пример 2. Решите логарифмическое неравенство:
![\[ \log_{x+1}(x^3+3x^2+2x)<2. \]](https://prezentacii.org/upload/cloud2/posts/2016-03/9/3/1/931435804.png){kind=small}
Решается учеником на доске с комментариями
Решение. Область допустимых значений неравенства определяется следующей системой:
![\[ \begin{cases} x+1>0, \\ x+1\ne 1,\\ x(x+1)(x+2)>0 \end{cases}\Leftrightarrow x\in (0;+\mathcal{1}). \]](https://prezentacii.org/upload/cloud2/posts/2016-03/1/3/3/1332066874.png)
Видно, что в области допустимых значений выражение, стоящее в основании логарифма, всегда больше единицы, а потому равносильным по теореме 2 будет переход к следующему неравенству:
![\[ x^3+3x^2+2x<x^2+2x+1\Leftrightarrow x^3+2x^2-1<0\Leftrightarrow \]](https://prezentacii.org/upload/cloud2/posts/2016-03/2/7/2/2725540185.png){kind=small}
![\[ (x+1)(x^2+x-1)<0\Leftrightarrow \]](https://prezentacii.org/upload/cloud2/posts/2016-03/2/4/2/2429965626.png){kind=small}
![\[ x\in\left(-\mathcal{1};-\frac{1+\sqrt{5}}{2}\right)\cup\left(-1;\frac{\sqrt{5}-1}{2}\right). \]](https://prezentacii.org/upload/cloud2/posts/2016-03/1/7/5/1753427696.png)
С учетом области допустимых значений получаем окончательный ответ:
![\[ x\in\left(0;\frac{\sqrt{5}-1}{2}\right). \]](https://prezentacii.org/upload/cloud2/posts/2016-03/1/6/2/1622818968.png)
Пример 3 .
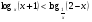
Решается учеником на доске с комментариями
Решение:
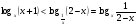
Данное неравенство равносильно системе рациональных неравенств:
x
-1
0
1
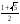
2
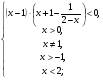
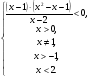
Ответ.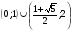 
.
Пример 4. Решите неравенство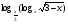 
≥ 0.
Решение. Заменим данное неравенство равносильной системой, используя метод рационализации
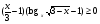
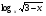> 0
3 – x > 0
x > 0
x ≠ 3
x ≠ 1
(x – 3)(x – 1)(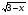
- 1) ≥ 0
(x – 1)(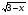- 1) > 0
x > 0
x ≠ 3
x ≠ 1
(x – 1)(3 – x –x2) ≤ 0
(x – 1)(3 – x – 1) > 0
x
x > 0
x ≠ 1
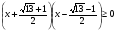
1 x
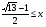
При решении неравенства (х – 1)(х – 2) x x > 0, x ≠ 1. Условие 1 x позволяет исключить множитель x – 1 > 0 в первом неравенстве системы.
Ответ: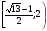 
.
Пример 5. Решите неравенство:
![\[ \frac{2\log_3(x^2-4x)}{\log_3 x^2}\leqslant 1. \]](https://prezentacii.org/upload/cloud2/posts/2016-03/1/7/3/1738885398.png)
Решение.
Область допустимых значений неравенства определяется системой неравенств:
![\[ \begin{cases} x^2-4x>0, \\ x^2>0, \\ x^2\ne 1 \end{cases}\Leftrightarrow x\in(-\mathcal{1};-1)\cup(-1;0)\cup(4;+\mathcal{1}). \]](https://prezentacii.org/upload/cloud2/posts/2016-03/4/5/1/451811472.png)
I способ. Воспользуемся формулой перехода к новому основанию логарифма и перейдем к равносильному в области допустимых значений неравенству:
![\[ \log_{x^2}(x^2-4x)^2\leqslant 1. \]](https://prezentacii.org/upload/cloud2/posts/2016-03/1/4/6/1465177854.png){kind=small}
Неравенство будет равносильно двум системам. Первой:
![\[ \begin{cases} x\in(-1;0), \\ (x^2-4x)^2\geqslant x^2 \end{cases}\Leftrightarrow \begin{cases} x\in(-1;0), \\ x^2(x-5)(x-3)\geqslant 0 \end{cases}\Leftrightarrow \]](https://prezentacii.org/upload/cloud2/posts/2016-03/1/1/4/1146903285.png)
![\[ x\in (-1;0). \]](https://prezentacii.org/upload/cloud2/posts/2016-03/1/9/5/1957027576.png){kind=small}
И второй:
![\[ \begin{cases}x\in(-\mathcal{1};-1)\cup(4;+\mathcal{1}), \\ x^2(x-5)(x-3)\leqslant 0 \end{cases}\Leftrightarrow x\in(4; 5]. \]](https://prezentacii.org/upload/cloud2/posts/2016-03/2/6/0/2601060344.png)
Итак, окончательный ответ:
![\[ x\in(-1;0)\cup(4;5]. \]](https://prezentacii.org/upload/cloud2/posts/2016-03/2/4/1/2411056823.png){kind=small}
II способ. Решаем методом интервалов. Преобразуем неравенство к виду:
![\[ \frac{2\log_3(x^2-4x)-\log_3 x^2}{\log_3 x^2}\leqslant 0\Leftrightarrow \]](https://prezentacii.org/upload/cloud2/posts/2016-03/3/2/9/3299541006.png)
Вычтем из знаменателя 
Это ничего не изменит, поскольку 
![\[ \frac{\log_3(x^2-4x)^2-\log_3 x^2}{\log_3 x^2-\log_3 1}\leqslant 0 \]](https://prezentacii.org/upload/cloud2/posts/2016-03/1/1/5/1159528355.png)
С учетом того, что выражения 
и 
— одного знака при 
в области допустимых значений имеет место следующий равносильный переход:
![\[ \frac{(x^2-4x)^2-x^2}{x^2-1}\leqslant 0\Leftrightarrow \]](https://prezentacii.org/upload/cloud2/posts/2016-03/1/5/2/1528467470.png){kind=small}
![\[ \frac{(x^2-5x)(x^2-3x)}{x^2-1}\leqslant 0. \]](https://prezentacii.org/upload/cloud2/posts/2016-03/1/3/3/1336946512.png){kind=small}
Множество решений данного неравенства
Итак, ![x\in(-1;1)\cup [3;5],](https://prezentacii.org/upload/cloud2/posts/2016-03/1/5/3/1534399379.png){kind=small}
а с учетом области допустимых значений получаем тот же результат: ![x\in(-1;0)\cup (4;5].](https://prezentacii.org/upload/cloud2/posts/2016-03/2/5/9/259646642.png){kind=small}
-
Подведение итогов урока. Рефлексия.
-
Домашнее задание.
-
Решите неравенство
.
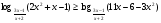Ответ: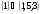 
-
Решите неравенство
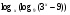
Ответ: (log310; +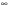 
).
-
Решите неравенство
.
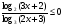Ответ: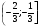 
.
Здесь представлен конспект к уроку на тему «РЕШЕНИЕ СЛОЖНЫХ ЛОГАРИФМИЧЕСКИХ НЕРАВЕНСТВ», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.
Список похожих конспектов
РЕШЕНИЕ НЕРАВЕНСТВ С ОДНОЙ ПЕРЕМЕННОЙ
КОНСПЕКТ УРОКА ПО АЛГЕБРЕ. В 8 КЛАССЕ. ТЕМА УРОКА: «РЕШЕНИЕ НЕРАВЕНСТВ С ОДНОЙ ПЕРЕМЕННОЙ». Современные образовательные технологии, применяемые ...
РЕШЕНИЕ НЕРАВЕНСТВ МЕТОДОМ ИНТЕРВАЛОВ
Конспект урока по алгебре. Тема урока: РЕШЕНИЕ НЕРАВЕНСТВ МЕТОДОМ ИНТЕРВАЛОВ. Цели урока:. образовательная: познакомить учащихся со способом ...
РЕШЕНИЕ УРАВНЕНИЙ С ПАРАМЕТРАМИ
Конспект урока на тему «РЕШЕНИЕ УРАВНЕНИЙ С ПАРАМЕТРАМИ». Задачи с параметрами часто встречаются на вступительных экзаменах по математике и столь ...
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Автор : Чирясова Наталия Константиновна. Место работы: ГОУ СОШ № 935, г. Москва. Должность: учитель математики. Дополнительные сведения: урок ...
РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Управление образования. Администрация Сергиево-Посадского района. Муниципальное бюджетное общеобразовательное учреждение. «Физико-математический ...