Конспект урока «РЕШЕНИЕ НЕРАВЕНСТВ МЕТОДОМ ИНТЕРВАЛОВ» по алгебре
Конспект урока по алгебре.
Тема урока: РЕШЕНИЕ НЕРАВЕНСТВ МЕТОДОМ ИНТЕРВАЛОВ
Цели урока:
-
образовательная: познакомить учащихся со способом решения неравенств методом интервалов с использованием свойств функции
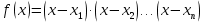
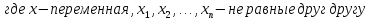 числа, являющиеся нулями функции;
числа, являющиеся нулями функции; -
воспитательная: воспитание познавательной активности, формирование творческого подхода к решению поставленной задачи, интереса к познавательному поиску;
-
развивающая: развитие логического мышления, внимания, познавательного интереса к предмету.
Оборудование: учебник, тетрадь, мультимедия.
Тип урока: комбинированный.
Ход урока:
I. Организационный момент (тема и цель)
II. Проверка домашнего задания (коррекция ошибок)
III.Устная работа (повторить формулы разности квадратов, умение раскладывать квадратный трёхчлен на множители)
IV.Изучение нового материала
Перед учащимися ставится задача: решить неравенство:
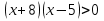 (№325а)
(№325а)
Рассуждаем: неравенство положительно, если оба множителя положительны или отрицательны одновременно. Значит надо решить две системы неравенств:
1)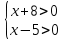
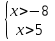
(5;+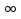 )
)
2)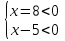
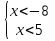
(-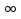 ;-8)
;-8)
Ответ: (-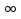 ;-8)
;-8)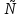 (5;+
(5;+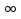 )
)
Решим другое неравенство:
(x-2)(x-5)(x-12)>0 (№327а)
Учащиеся понимают, что рассуждения о возможных знаках каждого из трёх множителей будут громоздкими, потому необходим другой метод решения.
Таким методом является метод интервалов.
Запись на доске, в тетради.
Если левая часть неравенства является произведением, а правая часть - о, то есть 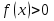
(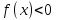 ) и
) и 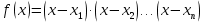 , где х -переменная,
, где х -переменная,
а 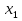 ,
, 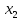 …,
…,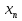 - не равные друг другу числа, то такие неравенства решаются методом интервалов.
- не равные друг другу числа, то такие неравенства решаются методом интервалов.
Числа 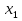 ,
, 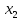 …,
…,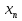 - нули функции. В каждом из промежутков, на которые область определения разбивается нулями функции, знак функции сохраняется, а при переходе через нуль её знак меняется.
- нули функции. В каждом из промежутков, на которые область определения разбивается нулями функции, знак функции сохраняется, а при переходе через нуль её знак меняется.
Для решения неравенства (x-2)(x-5)(x-12)>0 воспользуемся следующим алгоритмом.
На экране и в тетради (или карточки лежат на партах)
Алгоритм
-
Найти область определения функции
-
Найти нули функции
-
Отметить на координатной прямой интервалы, на которые область определения разбивается нулями функции
-
Определить знак функции на каждом промежутке (интервале)
-
Записать ответ
Решение
(x-2)(x-5)(x-12)>0
-
x
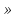 R
R -
(x-2)(x-5)(x-12)>0
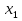 =2,
=2, 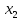 =-5,
=-5, 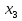 =12
=12
-
+
-
+
-5
2
12
-
(-5;2)
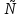 (12:+
(12:+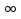 )
)
Решим первое неравенство методом интервалов:
(х+3)(х-5)>0
-
(х+3)(х-5)=0
-
х
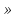 R
R -
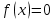 , если х = - 8 или х = 5
, если х = - 8 или х = 5
+
+
-
-8
5
Ответ: (-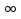 ;-8)
;-8)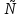 (5;+
(5;+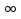 )
)
Рассмотреть примеры 2, 3 на странице 90 (учебник). В этих примерах до применения метода интервалов необходимо привести неравенства к стандартному виду (x на первом месте!)
V. Решение задач №325 (в, г), №327 (в).
VI. Итог урока:
-на каком свойстве функции основан метод интервалов? (при переходе через нуль знак функции меняется)
-неравенства какого вида можно решать методом интервалов, (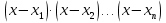 >0)
>0)
-повторить алгоритм решения неравенств методом интервалов.
VII. Домашнее задание: пункт 15, №326 (а, б), №328 (б), №329
Здесь представлен конспект к уроку на тему «РЕШЕНИЕ НЕРАВЕНСТВ МЕТОДОМ ИНТЕРВАЛОВ», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

