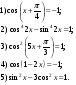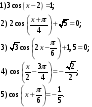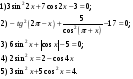Конспект урока «РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ» по алгебре для 10 класса
Управление образования
Администрация Сергиево-Посадского района
Муниципальное бюджетное общеобразовательное учреждение
«Физико-математический лицей»
РЕШЕНИЕ ПРОСТЕЙШИХ
ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Семинар – практикум по алгебре и началам анализа с применением групповых, информационно-коммуникационных образовательных технологий
10 класс
Учитель: Мрачковская Т.Г.
2013 - 2014 уч. г.
Тема урока: Решение простейших тригонометрических уравнений
Тип урока: урок формирования навыков и умений.
Цели урока: 1) формирование умений решения уравнения 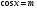 (частные, общий случаи);
(частные, общий случаи);
2) формирование умений записи ответа решения тригонометрического уравнения, содержащего функции сложного аргумента;
3) развитие навыков работы в коллективе, умений четко и математически грамотно
выражать свои мысли;
Применяемые обучающие технологии:
-
ИКТ;
-
педагогика сотрудничества (разбиение материала на блоки, взаимо и самоконтроль);
-
групповые;
-
тестовые;
-
здоровьесберегающие.
ХОД УРОКА
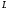 Проверка выполнения домашнего задания (взаимоконтроль)
Проверка выполнения домашнего задания (взаимоконтроль)
Выполнение домашнего задания проводится с использованием ИКТ (слайд 1): обучающиеся обмениваются тетрадями и проводят проверку решения задач.

Учитель выборочно выставляет оценку за выполнение работы.
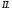 Теоретический диктант (ИКТ, тестовые технологии)
Теоретический диктант (ИКТ, тестовые технологии)
Диктант содержит теоретический материал, необходимый для проведения урока по темам:
-
«
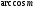 . Основные свойства»,
. Основные свойства», -
«Функция
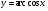 . Свойства»,
. Свойства», -
«Решение уравнения
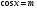 ».
».
Диктант проводится в режиме ограниченного времени на выполнение задания (слайды меняются автоматически)
-
Вопрос
Ответ
Время удержания слайда
1
Определение:
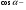
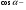 это абсцисса точки единичной тригонометрической окружности, которая соответствует данному углу поворота
это абсцисса точки единичной тригонометрической окружности, которая соответствует данному углу поворота40 с
2
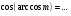
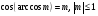
20 с
3
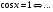
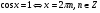
20 с
4
Определение:
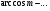
(записать символически)
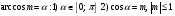
40 с
5
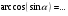
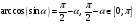
30 с
6
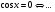
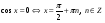
20 с
7
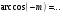
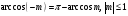
20 с
8
… - ось косинусов
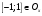 - ось косинусов
- ось косинусов20 с
9
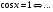
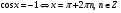
20 с
10
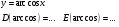
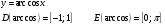
30 с
11
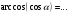
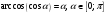
30 с
12
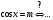
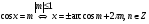
20 с
Время проведения диктанта
310 с=5м 10 с
Обучающимся предоставляется 1-2 м для самопроверки выполнения работы.
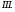 Решение простейших тригонометрических уравнений (групповые технологии)
Решение простейших тригонометрических уравнений (групповые технологии)
Обучающиеся подгруппы разбиваются на группы по 3 человека. Каждая группа составлена так, что в ней обязательно есть ученик, который владеет материалом (и теоретическим и практическими навыками) на достаточно хорошем уровне и всегда может оказать помощь в решении задачи.
Каждая группа получает задание (карточки) и приступает к анализу выполнения работы и самому решению уравнений:
1) устанавливает порядок решения задач (сначала номер блока, а затем порядок решения задач в самом блоке);
2) обсуждает различные подходы к решению уравнения (необходимые формулы преобразования, способы решения);
3) проводит самоконтроль записи решения уравнения и формированию ответа.
При выполнении задания обучающиеся могут пользоваться своими лекционными тетрадями, которые содержат примеры решения уравнений и их оформление.
Задание блока считается выполненным, если каждый обучающийся группы решил и выполнил запись решения каждого уравнения блока.
По окончании работы с блоком, группа сдает решение учителю. Учитель проверяет правильность решения и его оформление по тетради любого из учеников группы.
Если группа затрудняется самостоятельно выполнить решение задачи, то учитель проводит необходимую консультацию.
Перед выполнением задания, учитель еще раз обращает внимание обучающихся на формы записи ответов при решении тригонометрических уравнений, делает записи на доске:
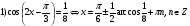
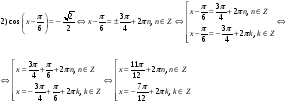
|
|
|
|
РЕШЕНИЕ
 Частные случаи
Частные случаи
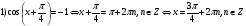
Ответ: 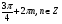
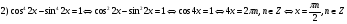
Ответ: 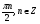
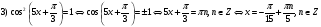
Ответ: 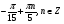
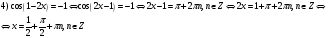
Ответ: 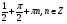
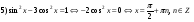
Ответ: 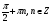
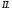 Общий случай
Общий случай
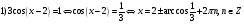
Ответ: 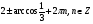
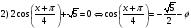
Ответ: 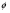
 Ответ:
Ответ: 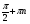 ,
, 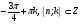
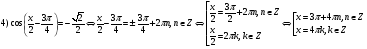 Ответ:
Ответ: 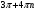 ,
, 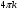 ,
,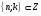
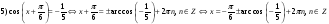
Ответ: 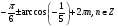
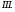 Уравнения, сводимые к алгебраическим
Уравнения, сводимые к алгебраическим
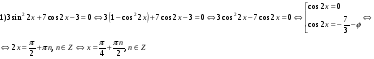 Ответ:
Ответ: 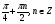
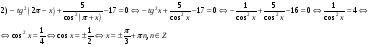 Ответ:
Ответ: 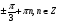
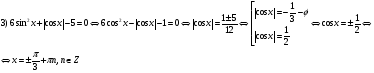
Ответ: 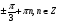
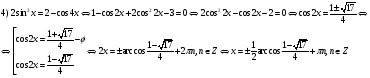
Ответ: 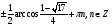
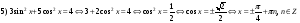
Следует обратить внимание на то, что ответ в решении уравнения может быть записан иначе: 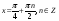
Ответ: 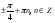
Домашнее задание:
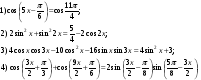
Здесь представлен конспект к уроку на тему «РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (10 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.