Конспект урока «Уравнение. Решение задач с помощью уравнения» по алгебре для 5 класса
Ф.И.О.: Шмитько Ирина Анатольевна
учитель математики
МБОУ гимназия № 40 г. Краснодара
г. Краснодар, ул. 2-я Пятилетка, 12
film.irina@yandex.ru
«География и математика: мультимедийный интегрированный урок (5-6 класс)»
Урок. Уравнение. Решение задач с помощью уравнения.
Цель урока: Закрепление нахождения компонентов в уравнениях. Решение задач на составление уравнений с использованием регионального компонента.
Оборудование: Планшет, сигнальные карточки, мультимедийное оборудование.
Ход урока.
На доске эпиграф:
«Любите Кубань, изучайте ее прошлое, созидайте будущее!
В добрый путь к новым познаниям! »
А. Н. Ткачев
-
Устные упражнения.
а)Учитель . На экране уравнения, в которых найден корень. Учащимся, с помощью сигнальных карточек, нужно определить, верно ли он найден.
Х + 12 = 32 Х = 19
Х + 15= 25 Х = 10
24 + Х = 31 Х = 7
45 – Y = 40 Y = 10
Y – 35 = 20 Y = 55.
(сигнальные карточки: «да» - зеленая, «нет» - красная)
б) Учитель математики предлагает восстановить цепочку вычислений:
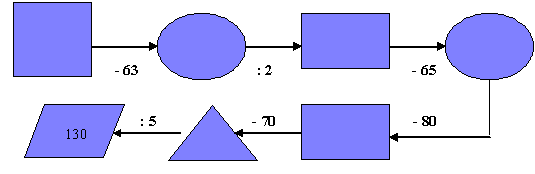
Решить на планшете и показать ответ учителю географии . Получится дата образования города.
Учитель задает вопрос: «Какого? Выберете из предложенных ниже вариантов».
Новороссийск – 1839 г.
Лабинск – 1841 г.
Краснодар – 1793 г
Вопрос:
Учитель . Как назывался Краснодар до 1920 года? (Екатеринодар)
Город Краснодар - центр Краснодарского края, расположен на правом берегу Кубани.
2. Работа по теме урока.
Задание № 1
На доске выписаны уравнения, которые учащиеся должны решить в тетради. Корни уравнения соответствуют буквам в таблице.
Учитель:
Расшифруйте название горы, расположенной на территории Краснодарского края и узнайте ее высоту.
1) Решите уравнения.
| B | C | d | |
| | | | |
| | | | |
b) (Y + 27) – 19 = 16
c) 6(Z - 3) = 18
d) (B + 5)2 = 24
2-Ф, 6- Ш, 7 – Т, 8 – И
Учитель рассказывает учащимся о горе Фишт.
.Задание № 2
Учитель предлагает решить задачу с помощью уравнения в тетради.

Путешествуя по ущелью, туристы прошли 108 м, что в 12 раз превышает высоту Большого Пшадского водопада. Найдите высоту водопада.
Решение: (4)
Пусть х м высота Большого Пшадского водопада. По условию задачи известно, что туристы прошли 108 м, что в 12 раз превышает его высоту (т. е. 12х).
Составим и решим уравнение:
12х = 108
х = 108 : 12
 х = 9
х = 9
12* 9 = 108
108 = 108
9 м – высота Большого Пшадского водопада.
Ответ: 9 м.
Учитель.
Путешественник, который отправится к этому водопаду в сильный мороз, обязательно должен сфотографировать его замерзшим, чтобы запечатлеть массивные ледяные колонны и причудливые гроты между ними. Это будет редчайшая удача.
Задание № 3 Учитель:
Найти длину реки Кубань от истока, если это число совпадает с корнем уравнения:
(Х + 94) : 5 = 200
Решение: Х + 94 = 200 * 5
Х + 94 = 1000
Х = 1000-94
 Х = 906
Х = 906
Проверка: (906 + 94) : 5 = 200
200 = 200
Длина реки Кубань от истока 906 км.
Учащиеся решают его в тетради с последующим комментарием учителя географии .
Длина реки Кубань от истока 906 км. Река в Ставропольском и Краснодарском Краях образуется слиянием рек Уллукам и Учкулам, берущих начало в районе города Усть – Лабинска, на склонах Эльбруса.
Задание № 4
Учитель предлагает учащимся устно решить задачу, вспомнив формулы нахождения скорости, времени и расстояния.
Автобус с учащимися гимназии № 40 выехал из города Краснодара в южном направлении в 8 часов утра. Двигаясь со скоростью 60 км/ч, в 9 часов утра пассажиры прибыли в пункт назначения. Найдите путь, пройденный автобусом, и назовите прекрасный уголок нашего края, куда прибыли пассажиры, если известно, что он знаменит минеральными источниками и скалой, носящей «птичье» название.
Решение:
Х : (9-8) = 60 1) 9 – 8 = 1(ч) были в пути пассажиры. Ответ: 60 км – путь, пройденный автобусом.
Учитель. Горячий Ключ знаменит санаториями, в которых поправляют свое здоровье не только жители нашего края, но и других городов. Здесь расположено Дантово ущелье, скала «Петушок», протекает живописная река Псекупс.
Составьте уравнение к задаче и устно решите его.
3. Повторение.
Учитель:
Узнать какой точке на координатном луче соответствует какая координата.
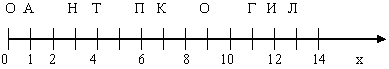
Результаты занести в таблицу.
| (13) | (1) | (4) | (9) | |
| | | | | |
| (1) | (11) | (9) | _ | (3) | (1) | (7) | (12) |
| | | | | | | | |
Ответ:
| (13) | (1) | (4) | (9) | |
| П | Л | А | Т | О |
| (1) | (11) | (9) | _ | (3) | (1) | (7) | (12) |
| Л | А | Г | О | Н | А | К | И |
Учитель:
Плато расположено на расстоянии 200 км от столицы Кубани. В районе плато находятся несколько десятков пещер, две из которых открыты для посещения туристами, пещеры «Нежная» и «Азишская».
Учитель.
4. Итог урока1. Что повторили на уроке? 2. Что нового узнали?
3. Учитель объявляет полученные результаты.
5. Домашнее задание.
1) В каком году был открыт памятник казакам – переселенцам и место, в котором он открыт, если:
а) 1, 3 и 4-я цифра совпадают.
б) вторая цифра в 9 раз больше каждой из оставшихся. (1911 г.)
2) Решите уравнения и узнайте место, где он был открыт.
М 1) 2Х + 7 = 17 (5)
Н 2) 3Y – Y – 4 = 0 (2)
Т 3) 10Х + 18 = 178 (16)
Ь 4) 13Z – 13 = 130 (11)
A 5) (31 – Х) : 9 + 8 = 11 (4)
Здесь представлен конспект к уроку на тему «Уравнение. Решение задач с помощью уравнения», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (5 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

