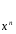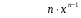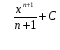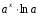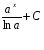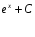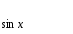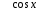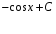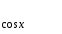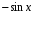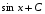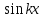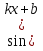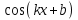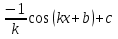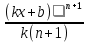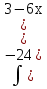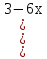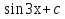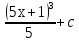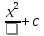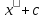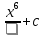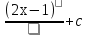Конспект урока «Производная и первообразная» по алгебре для 11 класса
Урок – соревнование: Производная и первообразная.
Клименко Ольга Андреевна, учитель математики 2 категории
Цель урока: повторение ранее изученного материала с целью качественной подготовки учащихся к сдаче единого национального тестирования.
Задачи урока:
Обучающие: формировать навыки прикладного использования аппарата производной;
выявить уровень овладения учащимися комплексом знаний и умений по вычислению производных функции и ликвидировать пробелы в знаниях в соответствии с требованиями к математической подготовке учащихся.
Развивающие: способствовать развитию умения сравнивать, обобщать, классифицировать, анализировать, делать выводы, развивать навыки коррекции собственной деятельности через применение информационных технологий.
Воспитывающие: побуждать учащихся само- и взаимоконтролю, воспитывать познавательную активность, самостоятельность, упорство в достижении цели.
Тип урока: обобщающий.
Методическое обеспечение занятия: раздаточный материал к уроку, интерактивная доска.
Опора на ранее полученные знания: формулы и правила нахождение производных и первообразных функций, тригонометрические формулы, формулы сокращённого умножения
ХОД УРОКА
-
Организационный момент
Вступительное слово учителя:
- Здравствуйте ребята и гости, я рада встрече с вами. Сегодня у нас урок необычный, урок-соревнование, и соревноваться вы будете не командами, не группами, как мы привыкли, а сами с собой. Чем выше будет полученный балл, тем выше оценка, а у некоторых их будет две.
Эпиграфом к уроку станут слова Аристотеля “УМ ЗАКЛЮЧАЕТСЯ НЕ ТОЛЬКО В ЗНАНИИ, НО И В УМЕНИИ ПРИМЕНЯТЬ ЗНАНИЯ НА ПРАКТИКЕ”.
-
Как вы понимаете смысл этих слов?
-
В какой ситуации вашей жизни вам приходилось применять ваши математические знания на практике?
Демонстрировать свои знания вы сегодня будете по теме “Производная и первообразная ”. Перед вами стоят задачи повторить, обобщить, закрепить ранее полученные знания с целью качественной подготовки к ЕНТ.
На партах у каждого из вас оценочный лист, в который вы будете заносить полученные вами балы за каждый пройденный этап.
Тот ученик, который выходит к доске для какого – либо объяснения получает бонус - красный жетон, который приравнивается к 1 баллу.
| Учебный элемент | Задание | Баллы | |
| Максимально баллов | Полученные баллы | ||
| УЭ1 | Заполнить пропущенные ячейки | 22 | |
| УЭ2 | Найди ошибку | 7 | |
| УЭЗ | Заполни пропущенные ячейки в вычислениях | 14 | |
| УЭ4 | Для данной функции вычисли производную и первообразную | 10 | |
| УЭ5 | Расшифруй кодировку | 7 | |
| УЭ7 | индивидуальная работа по решению заданий тестового характера из сборников для подготовки к ЕНТ | 5 – «5» 4 – «4» 3 – «3» | |
| УЭ7 * | Задание для эрудитов | | |
| Итого | 56 – 65 – «5» 49-55 – «4» 39-48 – «3» | | |
| Оценка за урок | |||
2. Актуализация имеющихся знаний
1 этап. У каждого на парте заготовлена таблица формул вычисления производных и первообразных, в которой не все ячейки заполнены. Задача каждого ученика восстановить записи.
| f`` (x) | F(x) | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| c | 0 | Kx+c |
|
|
|
|
|
| -k |
|
|
| k |
|
| (kx+b)n | nk(kx+b)n-1 |
|
|
| - |
|
После проделанной работы на экране доски появляется верно заполненная таблица, ученики производят взаимопроверку и полученные баллы заносят в оценочный лист.
3. Практическое применение знаний
2 этап. На экране интерактивной доски расположен флипчарт с решёнными заданиями. В каждом задании имеется ошибка в рассуждениях или в вычислениях. Найдите её и исправьте.
1. ![]()
2. ![]()
3. ![]()
4. ![]()
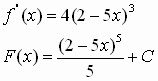
5. ![]()
![]()
6. ![]()
7. ![]()
Данную работу один ученик выполняет у доски, после проделанной работы комментирует .
3 этап. У вас на столах имеются решения примеров на нахождение неопределённого интеграла, но некоторые моменты в них пропущены. Заполните их:
| 2 вариант | |
| 1. | 1. |
| 2. | 2. |
| 3. | 3. |
| 4. | 4. |
| 5. | 5. |
| 6. | 6. |
| 7. | 7. |
| 8. | 8. |
| 9. | 9. |
| 10. | 10. |
| 2 вариант | |
| 1. | 1. |
| 2. | 2. |
| 3. | 3. |
| 4. | 4. |
| 5. | 5. |
| 6. | 6. |
| 7. | 7. |
| 8. | 8. |
| 9. | 9. |
| 10. | 10. |
После проделанной работы 10 учеников с каждого варианта заполняют пропущенные моменты в решениях с объяснением c места.
4 этап. На доске записаны пять функций. Задача учеников вычислить для них производную и первообразную. После выполненной работы в парах, пять учеников выходят к доске и объясняют ход решения.
-
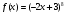
-
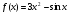
-
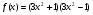
-
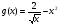
-
f (x) =
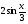
5 этап. Решив эти примеры, вы расшифруете фамилию французского математика, который ввел термин “производная”.
|
|
| |||||||
| Н |
|
| ||||||
| Г |
|
| ||||||
| А |
|
| ||||||
| Ж |
|
| ||||||
| А |
|
| ||||||
| Л |
|
| ||||||
|
|
| 10 | 5 |
|
| -1 | ||
| н | а | г | р | а | л | ж | ||
На доске высвечивается флипчарт с решениями и ответом. Ученики производят проверку своей работы и выставляют полученные баллы в оценочный лист.
6 этап Ученица класса проводит физминутку для снятия напряжения с глаз и активизации мозгового кровообращения.
Ученикам предлагается закрыть глаза и представить перед собой большой белый экран. Необходимо мысленно раскрасить этот экран поочерёдно любым цветом: например, сначала жёлтым, потом оранжевым, зелёным, синим, но закончить раскрашивание нужно самым любимым цветом.
7 этап Индивидуальная работа по решению заданий тестового характера из сборников для подготовки к ЕНТ. У каждого на парте имеется тест из 5 заданий. В течение девяти минут ученики самостоятельно прорешивают задания теста. После проделанной работы ученики заносят ответы при помощи оборудования активвод. На доске появляется процент выполнения теста каждым учеником. Данные результаты переводятся в баллы и заносятся в оценочный лист. После чего на экране доски появляется флипчарт с правильными решениями. В это время ученики, набравшие
« 5 » баллов, выполняют задание «для продвинутых».
-
Дана функция
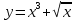 . Вычислить у' (х).
. Вычислить у' (х).
-
3х + 2
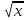
-
3х2 +
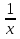
-
х +
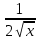
-
3х2 + 2
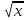
-
3х2 +
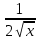
-
Найти производную функции у =
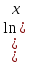
-
Первообразные функции у = 5

-
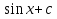
-
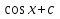
-
-
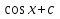
-
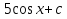
-
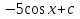
-
Найдите у' (
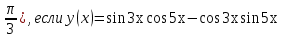
-
-1
-
1
-
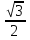
-
-
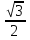
-
-
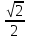
-
Найти у' (х), если у =
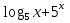
-
 +
+ 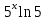
-
 +
+ 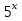
-
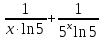
-
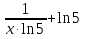
-
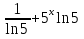
*Задание для продвинутых: ( действует с самого начала урока)
-
Найти производную функции у =
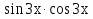
-
Вычислить первообразную для функции у = 6х2-4х+1
-
Вычислить производную для функции у =
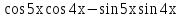
-
Вычислить производную для функции у =
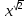
-
Вычислить значение производной при х = 5, если у = ( 4х+1)
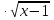
-
Вычислить первообразную для функции у =
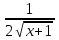 +
+ 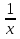
-
Вычислить производную для функции у =
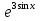
-
Вычислить первообразную для функции у =
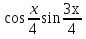
-
Вычислить производную для функции у =
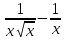
-
Вычислить производную для функции у = 3
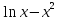
-
Вычислить производную для функции у =
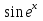
-
Вычислить производную в точке х = 0 для функции у =
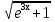
-
Вычислить первообразную для функции у =
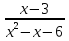
-
Вычислить производную для функции у =
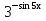
-
Вычислить производную для функции у =
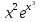
-
Вычислить производную для функции у = tg
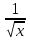
-
Вычислить производную для функции у = (
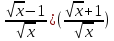
-
Вычислить производную для функции у = (2
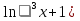 4
4
-
Вычислить производную для функции у =
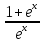
-
Вычислить производную для функции у =
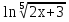
8 этап Подведение итогов урока. Оценивание.
Здесь представлен конспект к уроку на тему «Производная и первообразная», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (11 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.