Конспект урока «Практические приложения производной» по алгебре для 10 класса
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа № 22
с углубленным изучением отдельных предметов
города Тамбова
Урок
на тему
Практические
приложения производной
10 класс
Учитель математики
Залипаева А.И.
Тема урока. Практические приложения производной.
Тип урока: урок обобщения и систематизации знаний.
Цель урока.
-
повторить определение производной;
-
выяснить, в чем состоит геометрический и физический смысл производной;
-
повторить формулы и правила дифференцирования;
-
рассмотреть в группах примеры заданий на приложение производной в других областях знаний (физика, химия, биология, экономика, техника, производство).
Оборудование.
-
Таблица «Формулы дифференцирования».
-
Таблица «Правила дифференцирования».
-
Компьютерная презентация «Ученые, внесшие вклад в развитие понятия производной».
-
Система упражнений.
Ход урока.
-
Оргмомент (2 мин).
-
Устная работа (7 мин).
-
Решение задач (25 мин).
-
Компьютерная презентация (5 мин).
-
Домашнее задание (3 мин).
-
Подведение итогов урока (3 мин).
Оргмомент.
Класс разбит на 4 группы. Каждой группе в процессе урока будет предложено задание из различных областей знаний:
-
математика;
-
физика;
-
экономика и производство;
-
химия, биология, экология.
Здравствуйте. Садитесь, пожалуйста. Запишите в тетрадях число и тему урока, которая указана на доске: «Практические приложения производной». На уроке мы постараемся представить вопрос о практических приложениях производной. В школьном курсе алгебры и начал анализа рассматриваются приложения только в смежных областях знаний – физике и геометрии, исходя из физического и геометрического смысла производной. Поэтому, рассмотрев вопрос о дифференцировании функции, мы попытались перейти к решению задач из областей знаний, далеких от математики – таких как экономика, производство, биология, химия, технология.
Так как математическое моделирование реальных процессов используют в различных областях знаний, то и производную можно применить не только в физике и геометрии.
Опыт решения задач такого вида пока небольшой, но на начальном этапе изучения производной соответствующие задания имеет смысл рассмотреть, с дальнейшим их усложнением.
Работу на уроке мы построим следующим образом:
-
Разминка в виде решения устных заданий на применение формул и правил дифференцирования.
-
Работа в группах по приложению производной в математике; физике; экономике и производстве; химии, биологии, экологии с представлением решения одной задачи от группы на доске с объяснением и проверкой.
-
Компьютерная презентация: исторический материал об ученых, внесших вклад в развитие производной.
-
Комментарий по выполнению домашнего задания.
-
Подведение итогов урока.
Переходим к осуществлению плана работы на уроке.
Устная работа.
-
Найдите производные указанных функций (если будет допущена ошибка, постарайтесь ее корректно исправить):
-
Найдите критические точки функции:
-
Верно ли, что ускорение тела происходит по линейному закону:
![]()
![]()
Решение задач.
Представитель каждой группы выбирает область знаний по билетикам.
| | физика | | экономика и производство | | химия, биология, экология |
Каждой группе предлагается 5 заданий. Их необходимо выполнить, решение оформить в тетради, обсудить и предоставить решение одной задачи на доске.
ЭКОНОМИКА
-
Функция полных издержек производства имеет вид
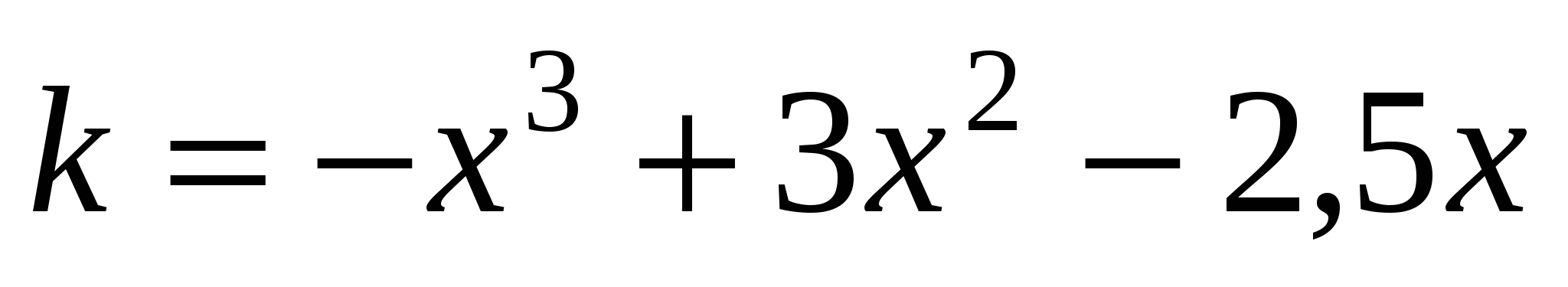 , где
, где 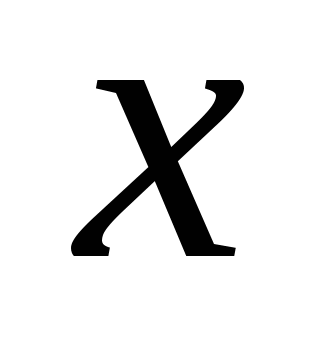 - объем производства продукции в условных единицах для данного производства. Определите, при каком объеме производства продукции средние издержки производства будут иметь наибольшее значение?
- объем производства продукции в условных единицах для данного производства. Определите, при каком объеме производства продукции средние издержки производства будут иметь наибольшее значение? -
Потребление электроэнергии предприятиями и населением города с 8 ч до 18 ч описывается формулой
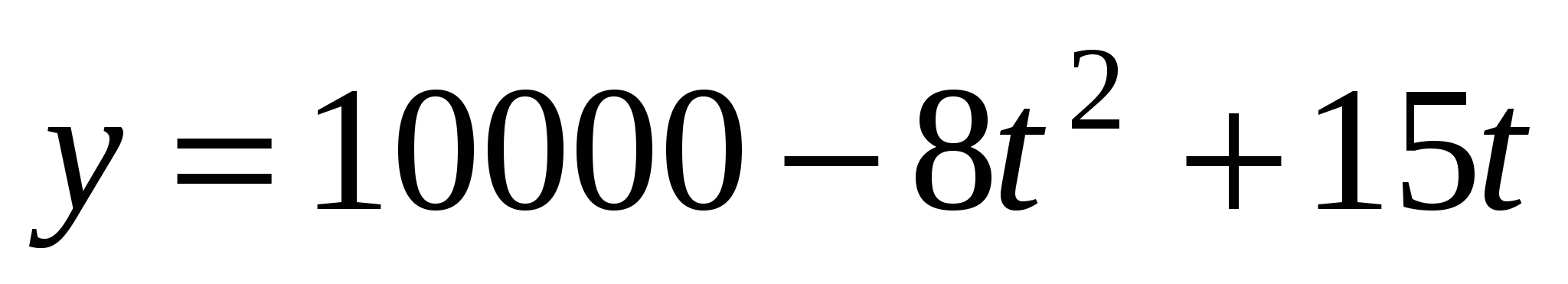 , где
, где 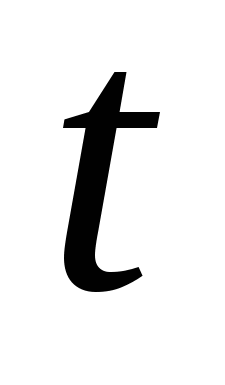 - время в часах. В какой момент времени потребление энергии будет наибольшим?
- время в часах. В какой момент времени потребление энергии будет наибольшим? -
Выручка магазина меняется в зависимости от сезона по формуле
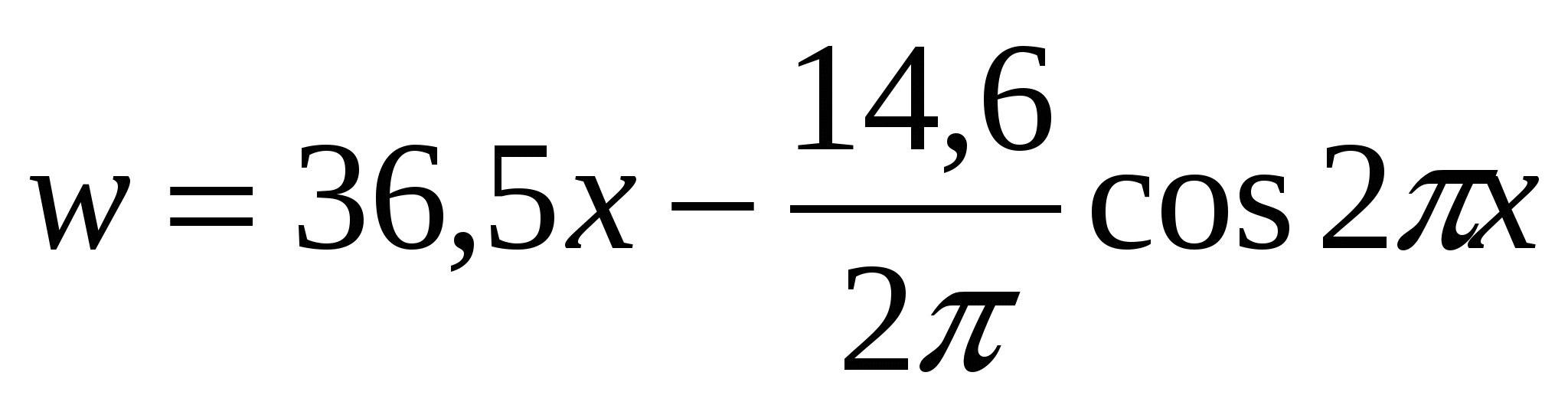 . Найдите закон изменения дневной выручки магазина (скорость изменения выручки).
. Найдите закон изменения дневной выручки магазина (скорость изменения выручки). -
Стоимость эксплуатации оборудования меняется по закону
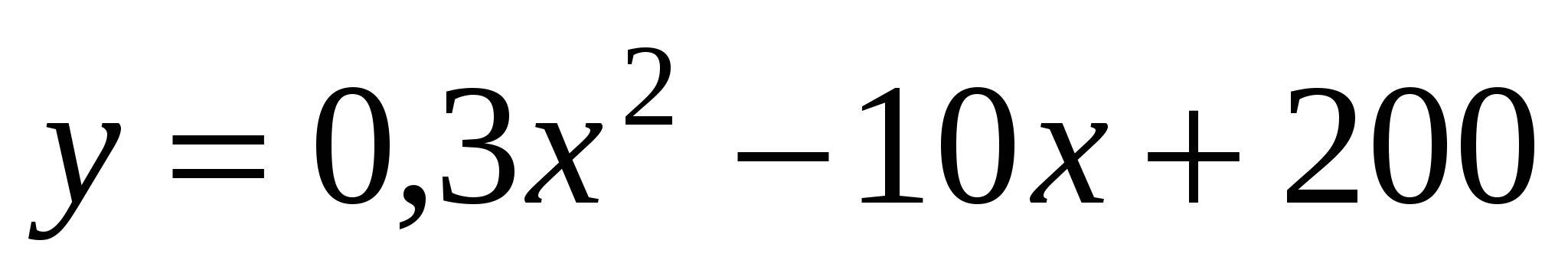 , где
, где 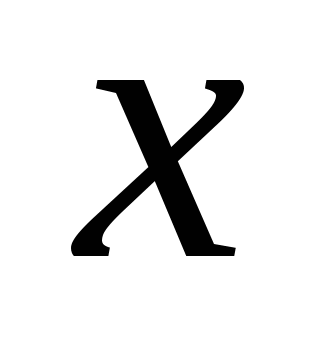 - время в годах. В какой момент времени стоимость эксплуатации будет наименьшей?
- время в годах. В какой момент времени стоимость эксплуатации будет наименьшей? -
Стоимость эксплуатации катера, плывущего со скоростью
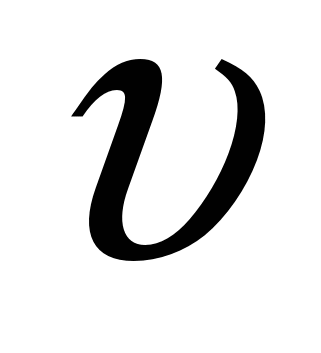 км/ч, составляет
км/ч, составляет 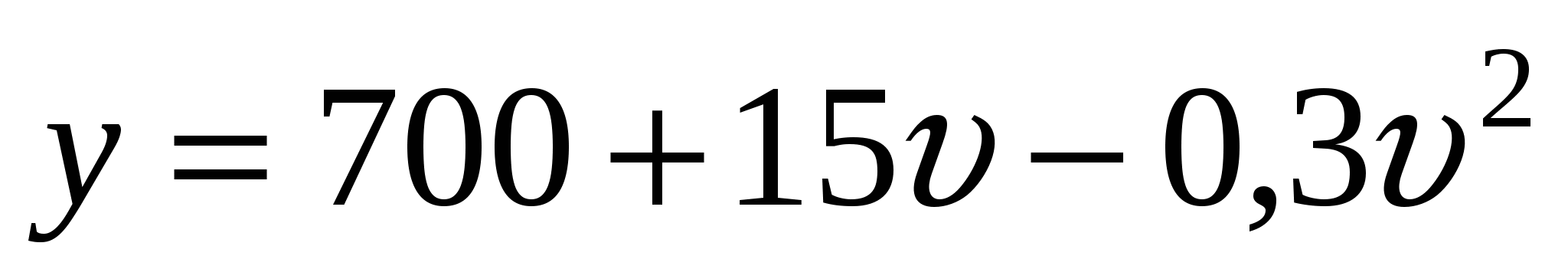 . С какой скоростью должен плыть катер, чтобы стоимость 1 км пути была наибольшей?
. С какой скоростью должен плыть катер, чтобы стоимость 1 км пути была наибольшей?
ФИЗИКА
-
Высота камня, брошенного вертикально вверх со скоростью
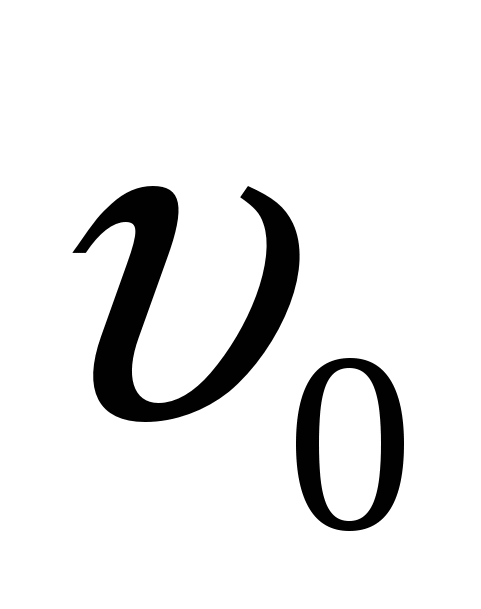 меняется по закону
меняется по закону 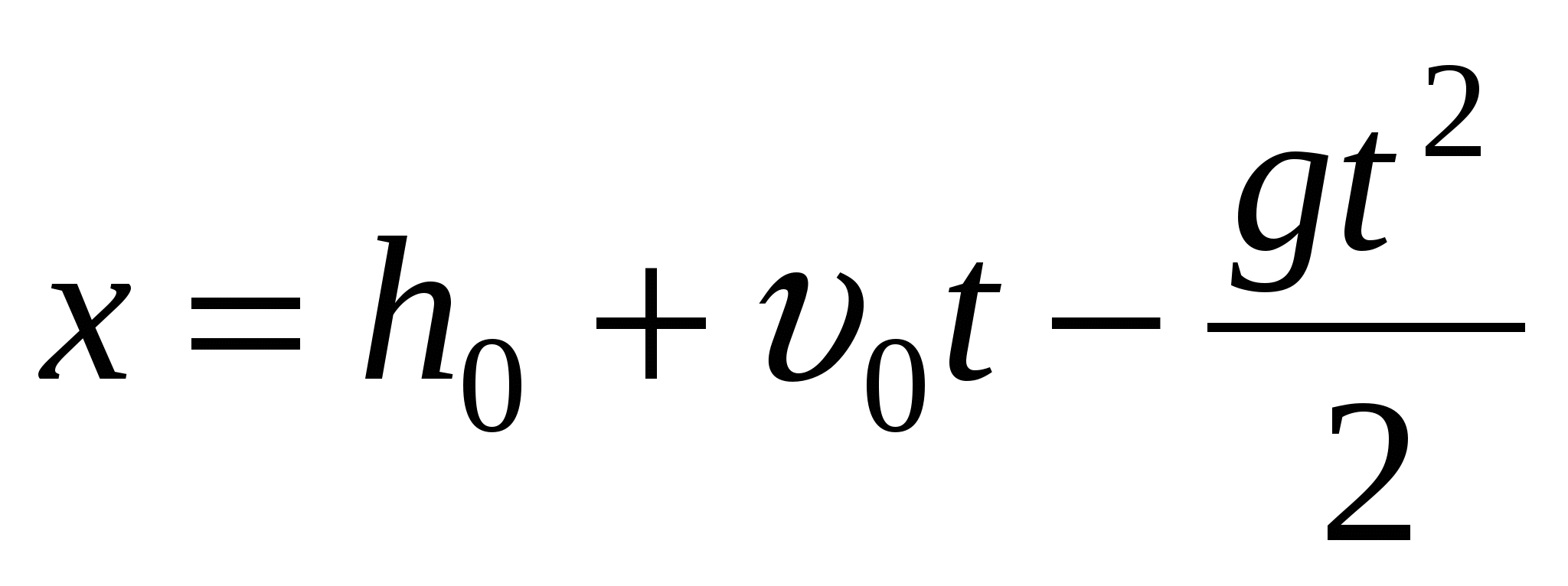 . Найдите зависимость скорости камня от времени.
. Найдите зависимость скорости камня от времени. -
Докажите, что движение по закону
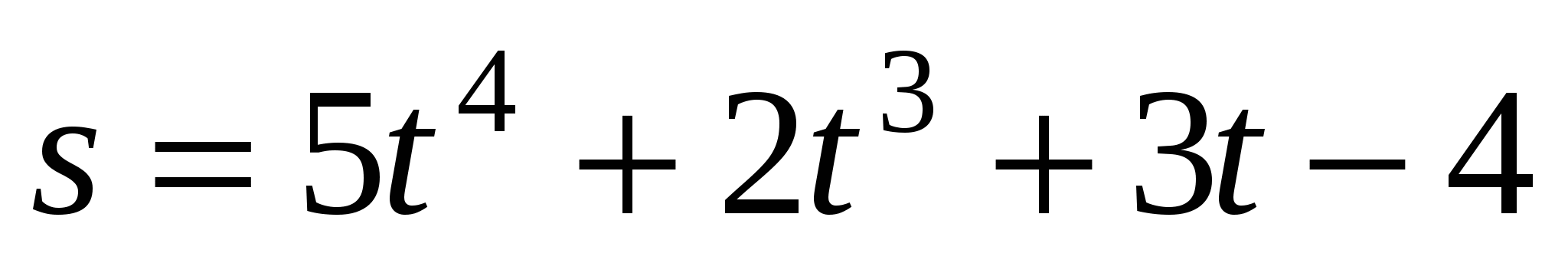 происходит с ускорением, меняющемся по квадратичному закону.
происходит с ускорением, меняющемся по квадратичному закону. -
Материальная точка движется по закону
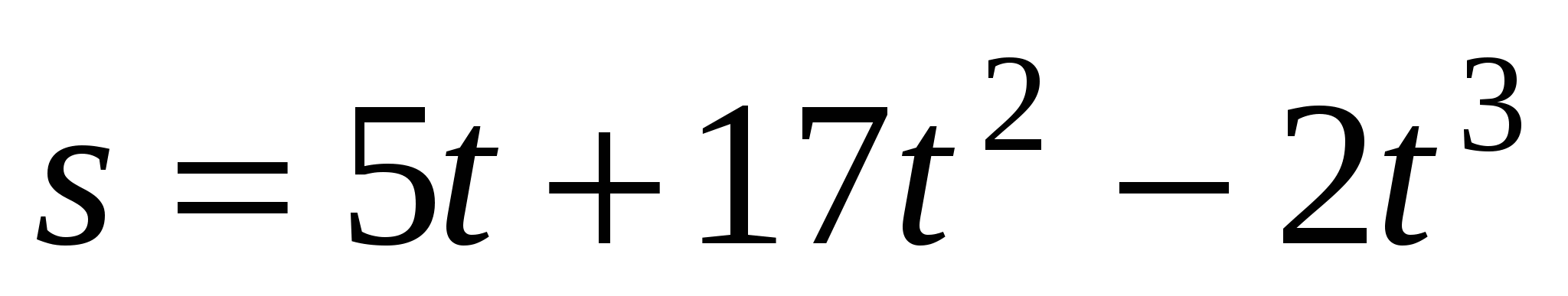 . Найдите ускорение в момент времени
. Найдите ускорение в момент времени 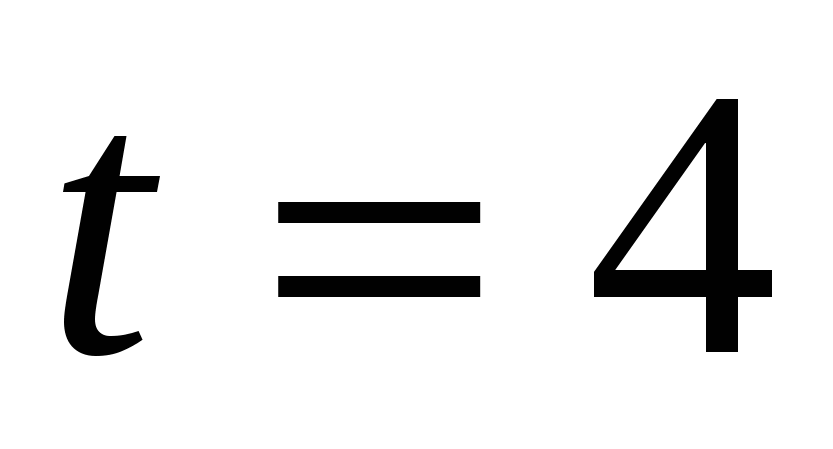 .
. -
Закон движения тела имеет вид
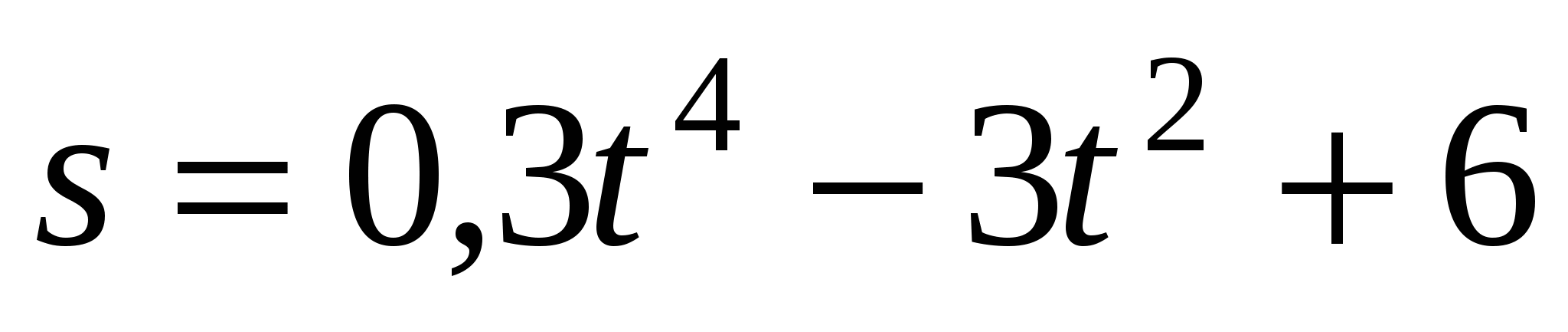 . Найдите момент остановки этого тела.
. Найдите момент остановки этого тела. -
Точка движется прямолинейно по закону
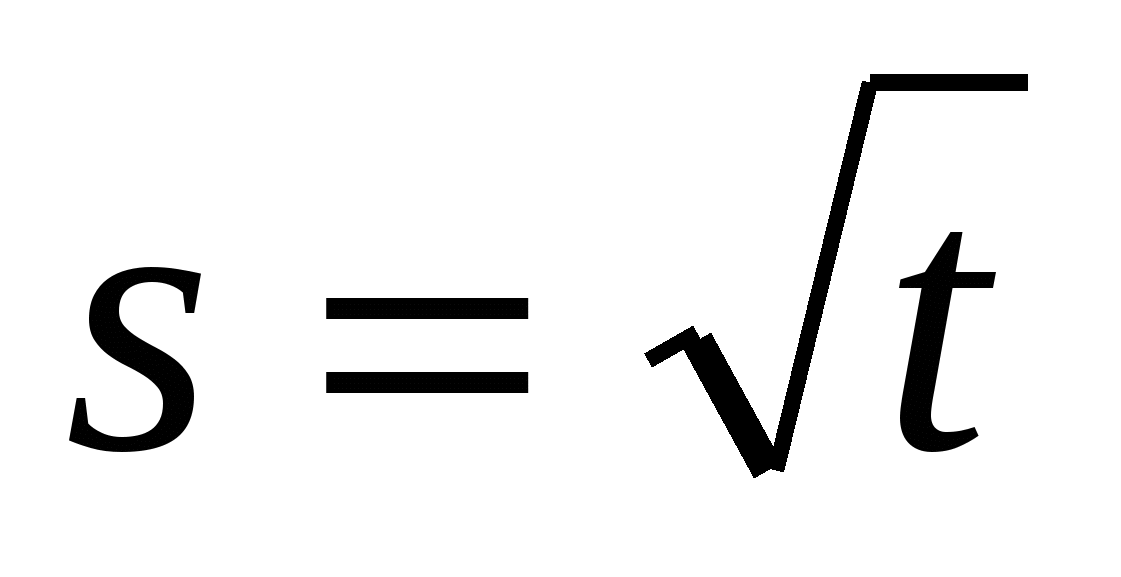 . Докажите, что движение замедленное.
. Докажите, что движение замедленное.
МАТЕМАТИКА
-
Составьте уравнение касательной к графику функции
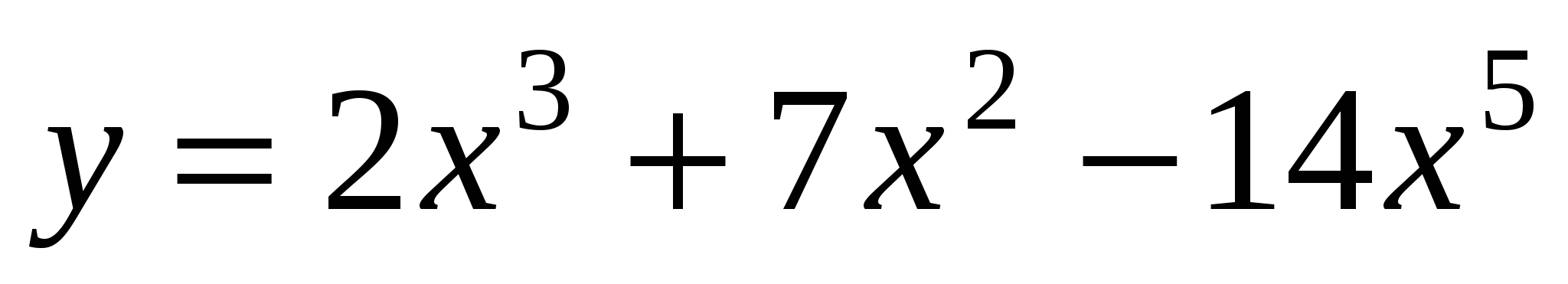 в точке
в точке 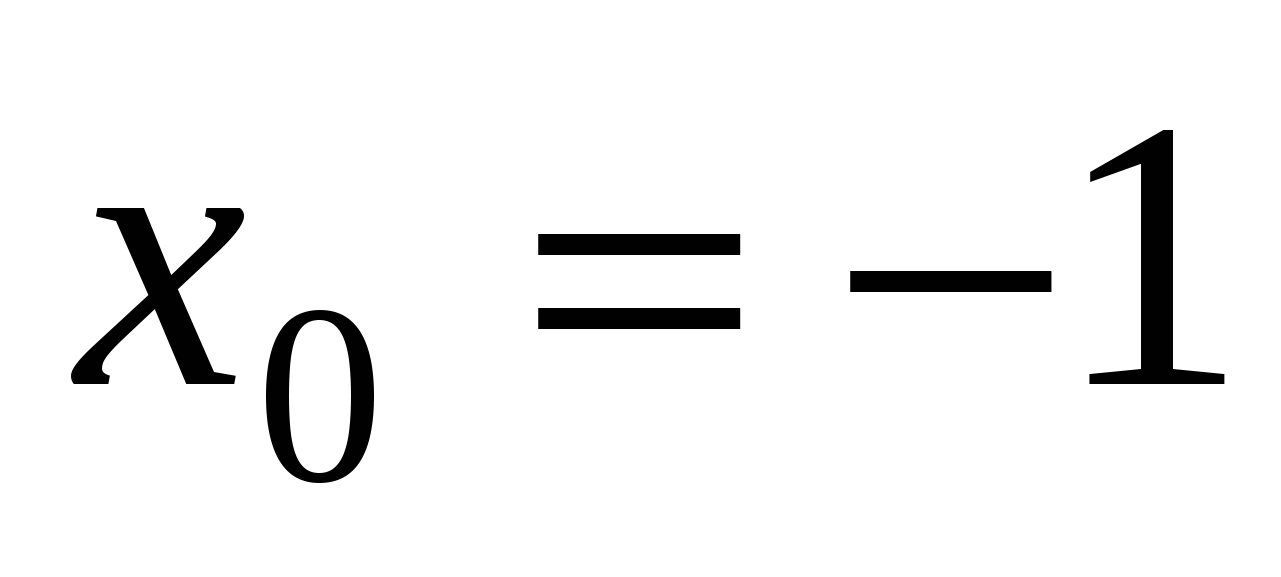 .
. -
Составьте уравнение касательной к графику функции
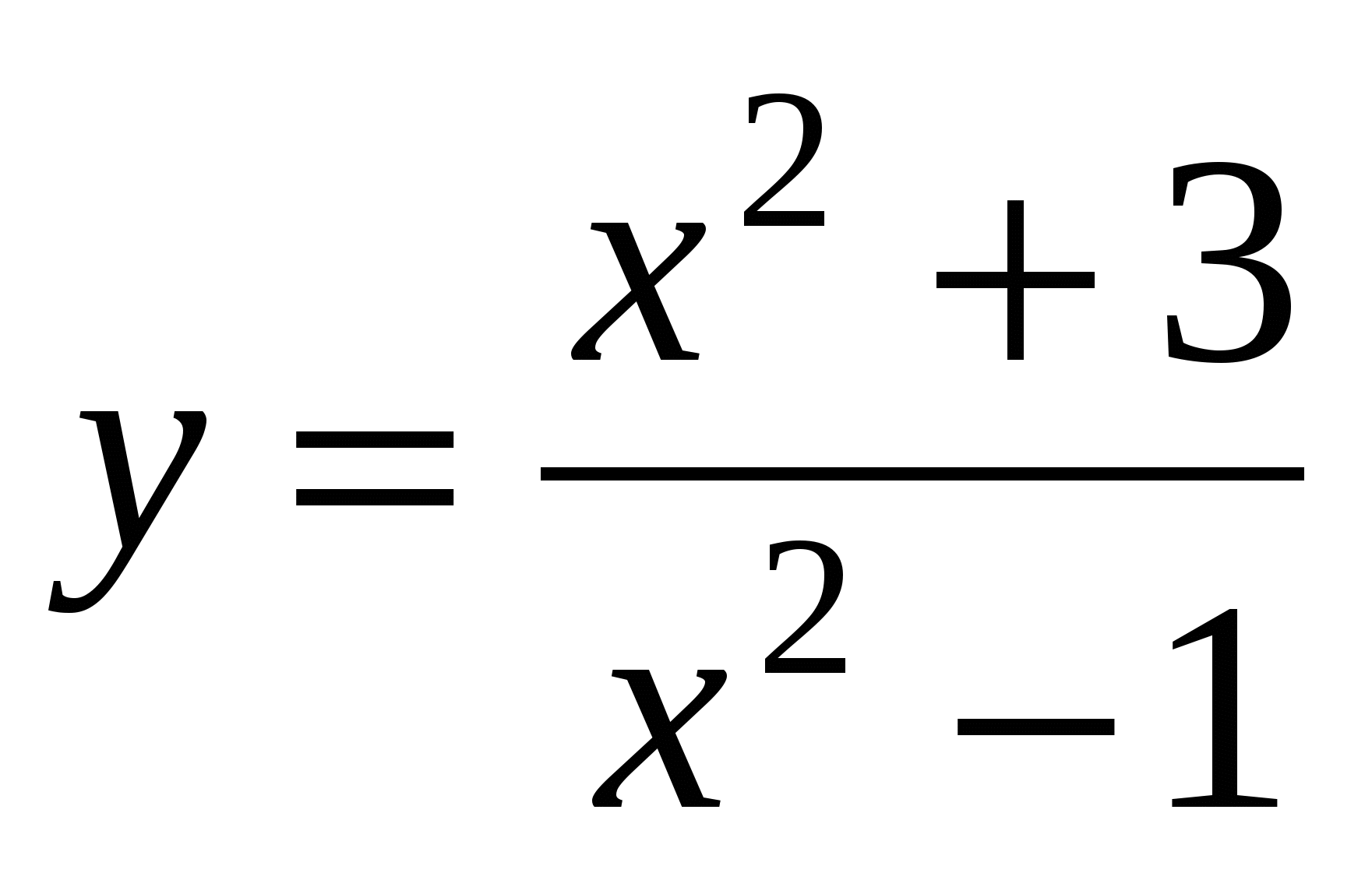 в точке
в точке 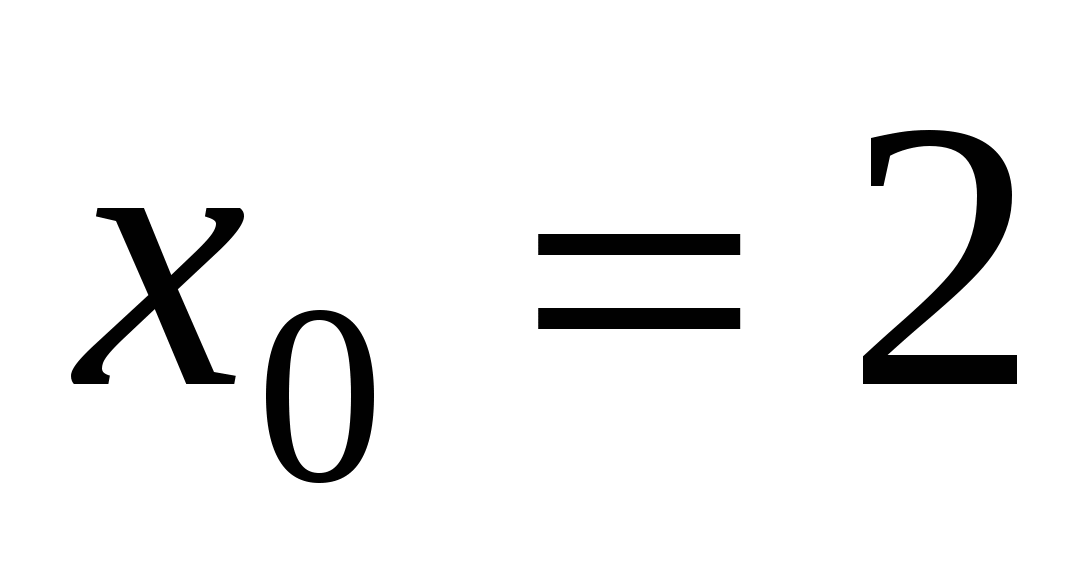 .
. -
Площадь прямоугольника 36 см2. Какую длину должны иметь стороны этого прямоугольника, чтобы его периметр был наибольшим?
-
Сумма двух чисел равна 24. Найдите эти числа, если их произведение принимает наибольшее значение.
-
Одно из двух чисел на 10 меньше другого. Найдите эти числа, если их произведение принимает наименьшее значение.
БИОЛОГИЯ, ХИМИЯ, ЭКОЛОГИЯ
-
В условиях экологического равновесия популяция хищников меняется по закону
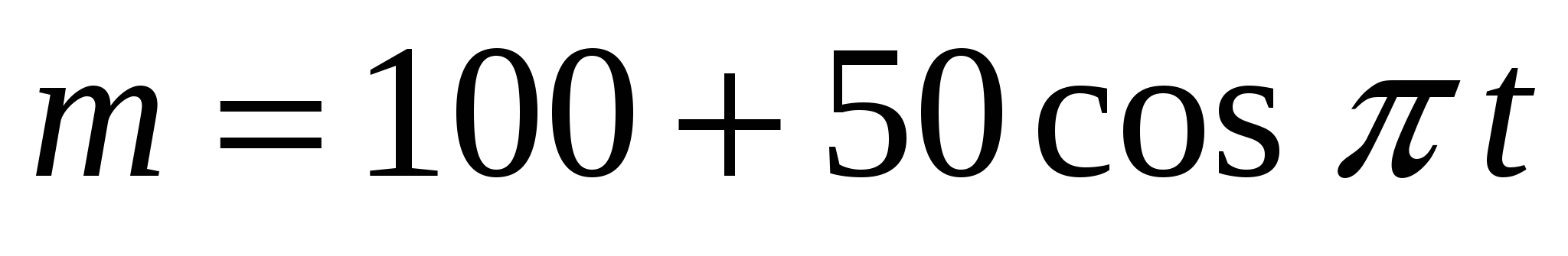 , где
, где 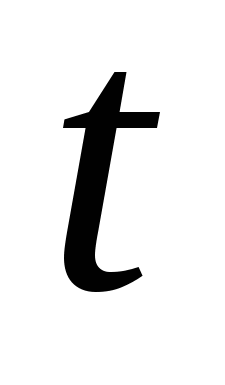 - время в годах. Найдите моменты времени, когда популяция хищников будет наибольшей и наименьшей.
- время в годах. Найдите моменты времени, когда популяция хищников будет наибольшей и наименьшей. -
В условиях экологического равновесия популяция травоядных жертв хищников меняется по закону
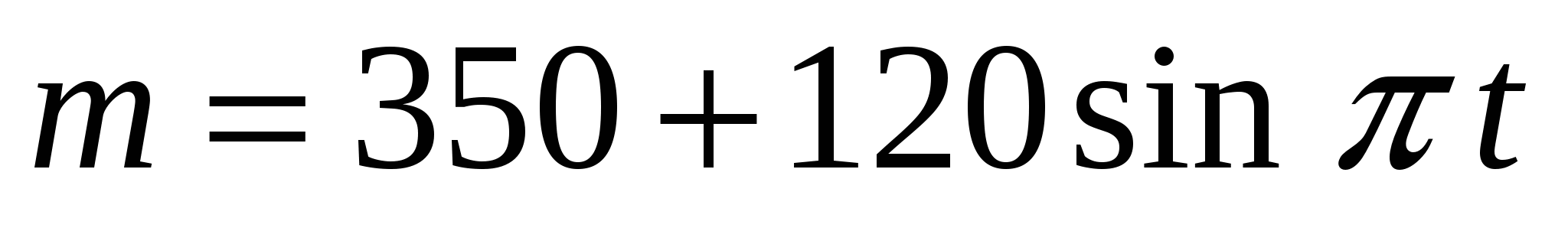 , где
, где 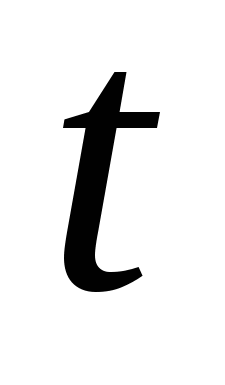 - время в годах. Найдите моменты времени, когда популяция травоядных жертв хищников будет наибольшей и наименьшей.
- время в годах. Найдите моменты времени, когда популяция травоядных жертв хищников будет наибольшей и наименьшей. -
В задачах 1. и 2. выясните, когда популяции хищников и травоядных жертв хищников будут равными.
-
Зависимость плотности
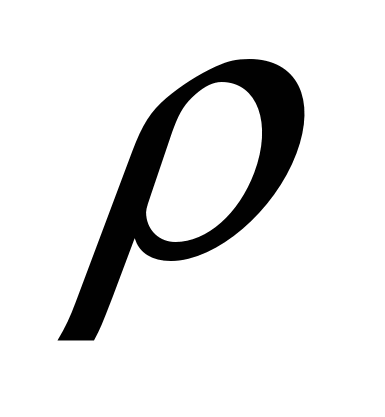 азотной кислоты от ее концентрации
азотной кислоты от ее концентрации 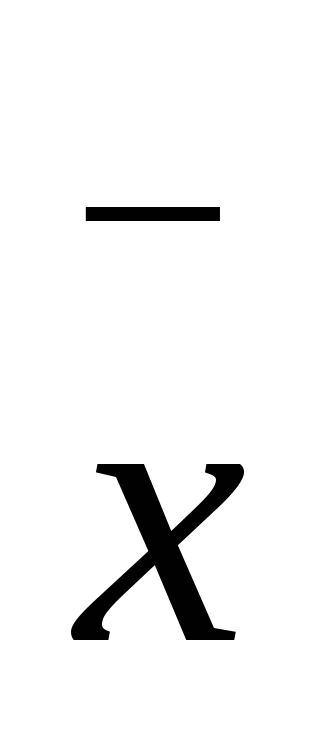 при комнатной температуре описывается эмпирической формулой
при комнатной температуре описывается эмпирической формулой 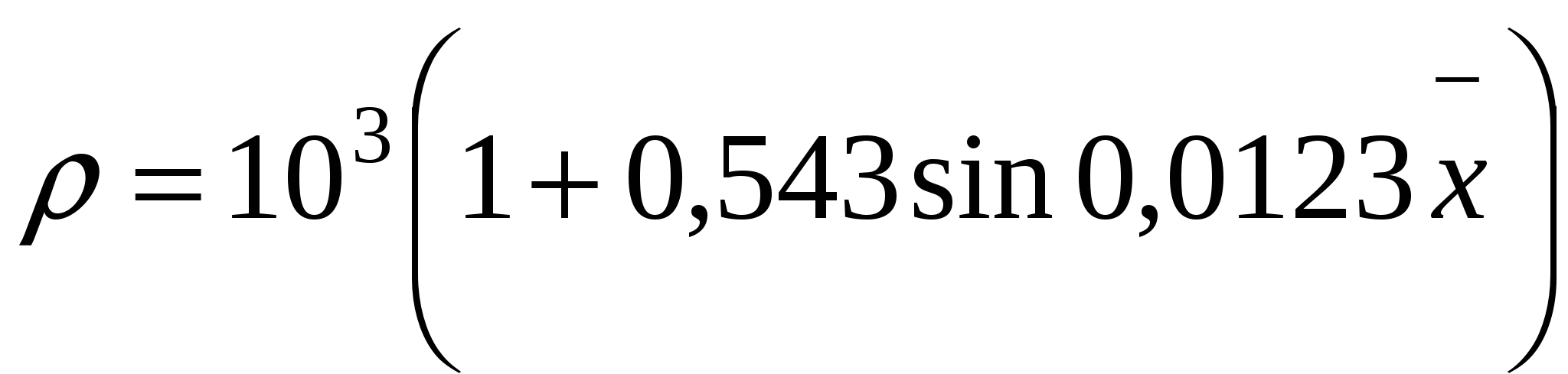 . Найдите закон изменения плотности
. Найдите закон изменения плотности 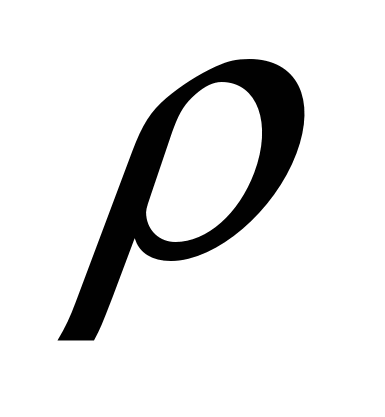 азотной кислоты.
азотной кислоты. -
Процент
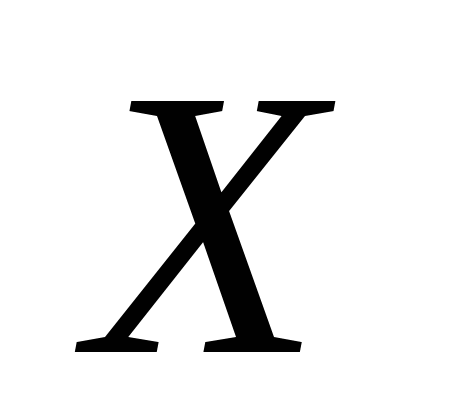 электропроводности раствора кислоты при комнатной температуре зависит от процента ее концентрации
электропроводности раствора кислоты при комнатной температуре зависит от процента ее концентрации 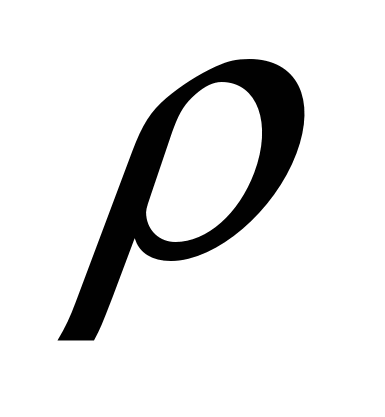 в соответствии с формулой
в соответствии с формулой 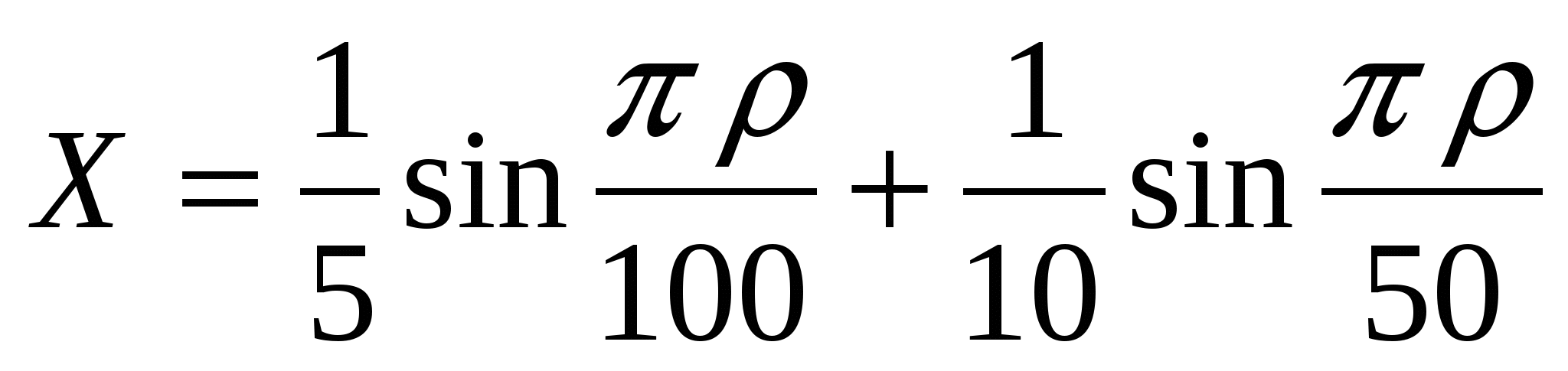 , где
, где 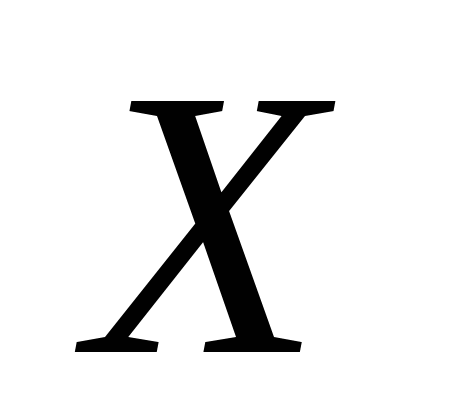 и
и 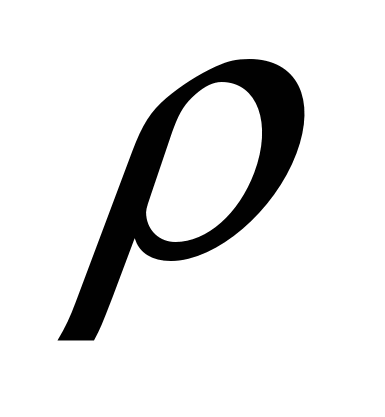 измеряются в процентах. При каком значении
измеряются в процентах. При каком значении 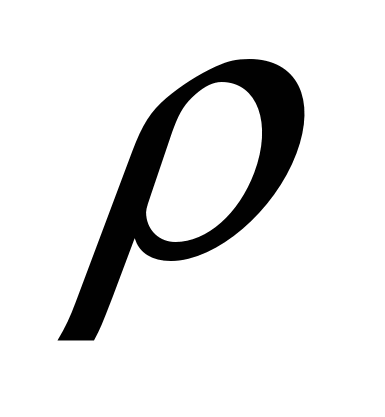 процент электропроводности
процент электропроводности 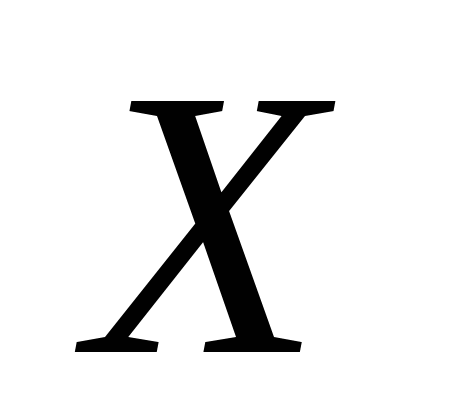 достигает наибольшего значения?
достигает наибольшего значения?
Представление задач на доске.
Компьютерная презентация.
Домашнее задание.
Поменяться заданиями группам. Сдать тетради на проверку. На следующих уроках в качестве заданий будут предложены подобные упражнения и у каждого ученика будет зачетная оценка по решению задач из каждой области знаний.
Подведение итогов урока.
Объявление оценок, полученных на уроке. На дополнительной доске необходимо указать ответы ко всем задачам, предлагавшимся к решению.
Приложение 1
К уроку в виде домашней работы были предложены следующие упражнения по данной теме:
РАБОТА, ПРОИЗВОДСТВО, ТЕХНОЛОГИЯ
-
Завод выполняет заказ, осваивая объем во времени согласно формуле
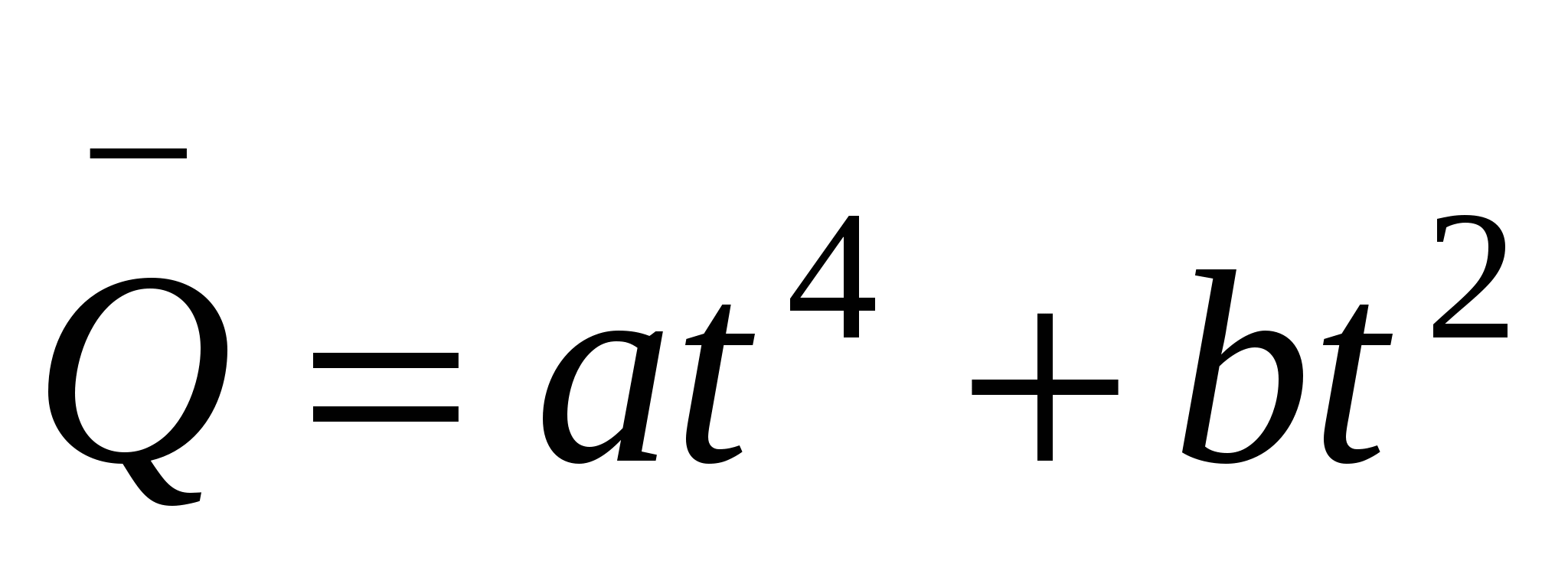 , где
, где 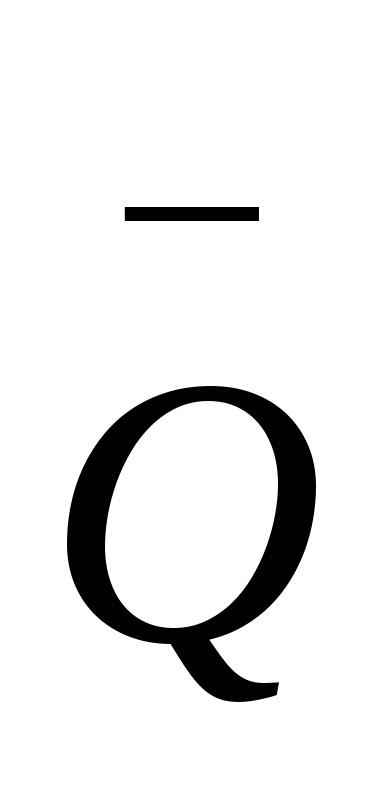 - выражается в %,
- выражается в %, 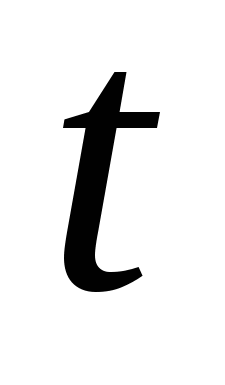 - в сутках.
- в сутках.
а). Какова интенсивность (скорость) работы на объекте (в % в сутки)?
б). Какова наименьшая интенсивность и в какой момент она имеет место?
-
Потребность в изделиях фабрики носит сезонный характер и определяется формулой
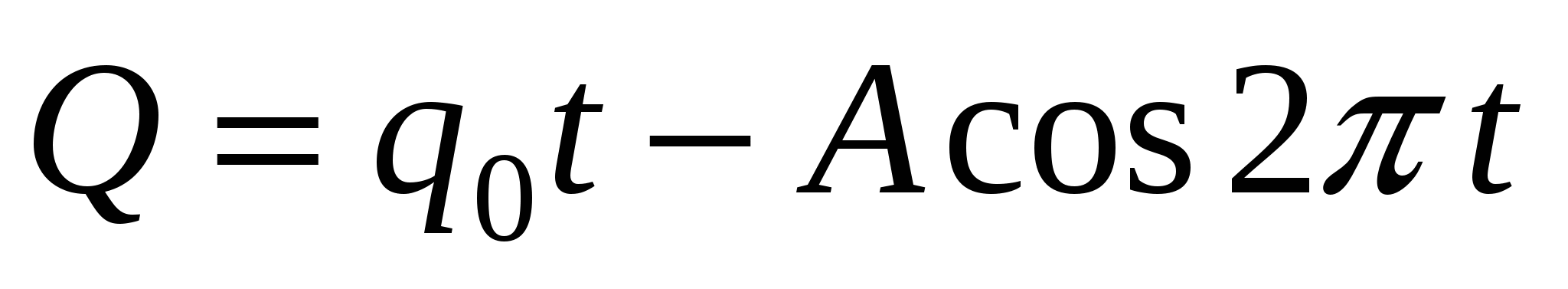 , где
, где  - общее количество (объем) изделий, выпущенных за время
- общее количество (объем) изделий, выпущенных за время 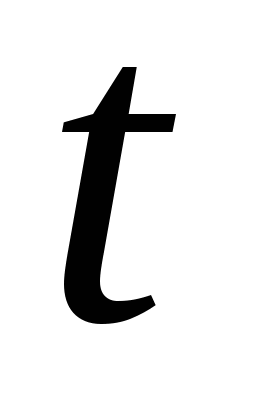 (единица времени 1 год). Какова наибольшая и наименьшая скорость выпуска изделий в сутки в течение года, и в какие моменты она достигается?
(единица времени 1 год). Какова наибольшая и наименьшая скорость выпуска изделий в сутки в течение года, и в какие моменты она достигается?
ФИЗИКА
-
Тело удаляется от Земли по закону
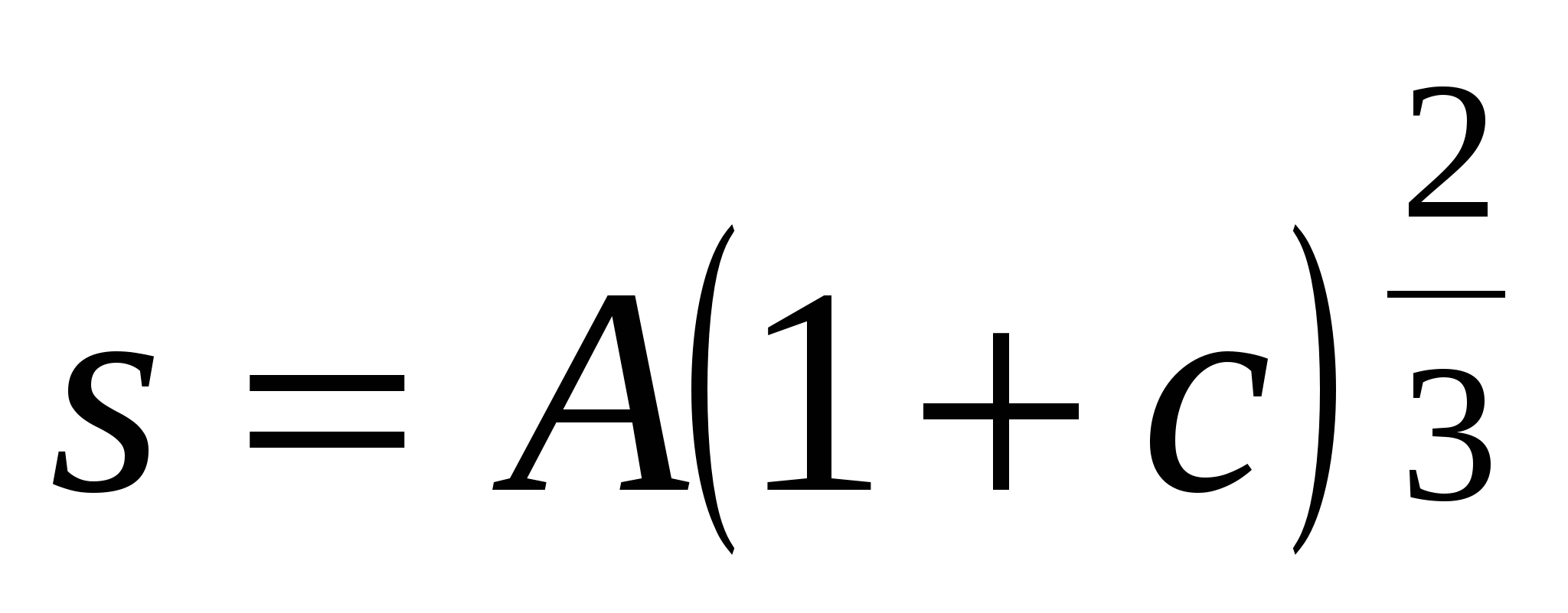 . Запишите закон, по которому меняется его скорость. Вычислите ускорение тела.
. Запишите закон, по которому меняется его скорость. Вычислите ускорение тела. -
Докажите, что движение по кубическому закону
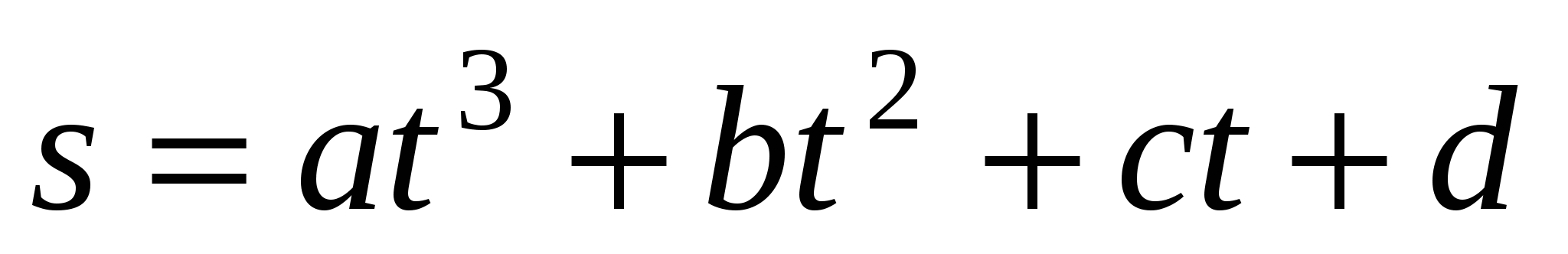 происходит с ускорением, меняющемся линейно.
происходит с ускорением, меняющемся линейно. -
Задан закон движения тела
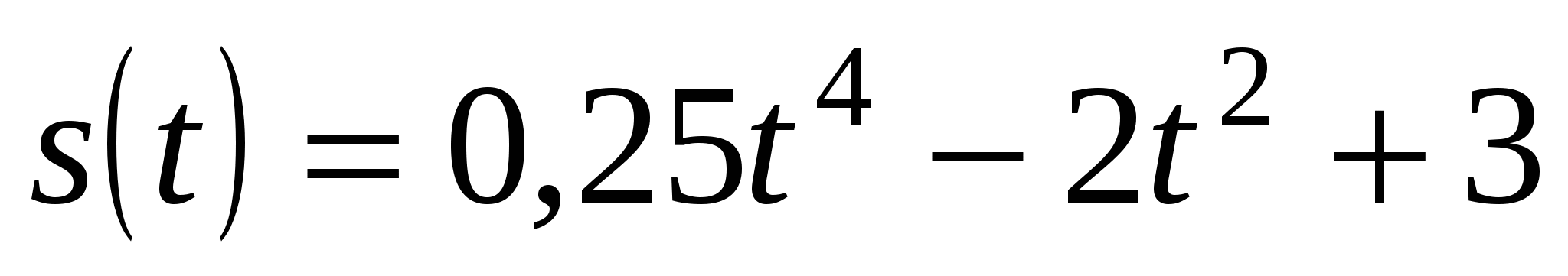 . Найдите моменты его остановки.
. Найдите моменты его остановки.
ЭКОНОМИКА
-
Функция полных издержек производства имеет вид
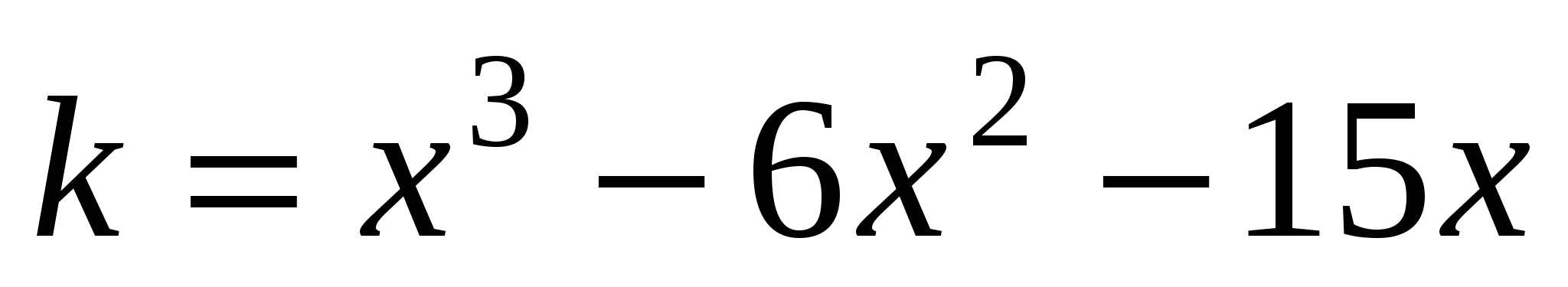 , где
, где 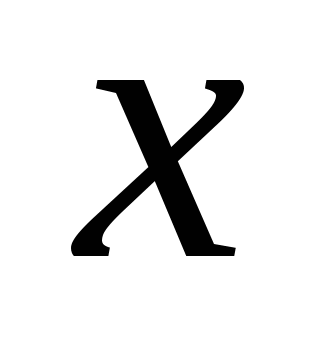 - объем производства продукции в условных единицах для данного производства. Определите, при каком объеме производства продукции средние издержки производства имеют наименьшее значение.
- объем производства продукции в условных единицах для данного производства. Определите, при каком объеме производства продукции средние издержки производства имеют наименьшее значение. -
Стоимость эксплуатации катера, плывущего со скоростью
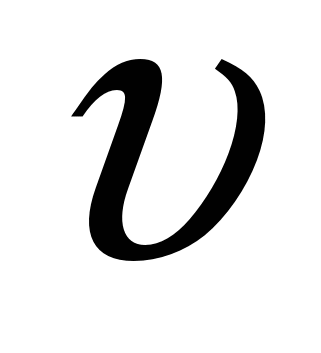 км/ч, составляет
км/ч, составляет 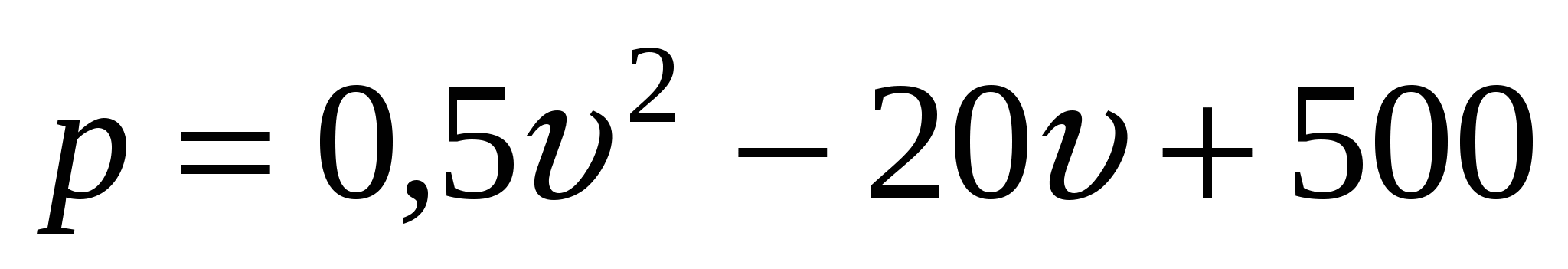 руб/ч. С какой скоростью должен плыть катер, чтобы стоимость 1 км пути была наименьшей?
руб/ч. С какой скоростью должен плыть катер, чтобы стоимость 1 км пути была наименьшей?
БИОЛОГИЯ, ХИМИЯ
-
Процент
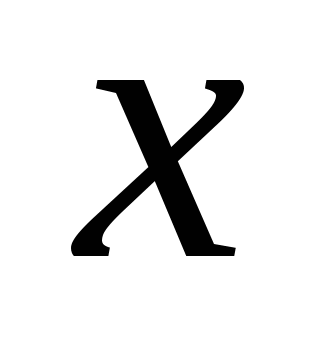 электропроводности раствора кислоты при комнатной температуре зависит от процента ее концентрации
электропроводности раствора кислоты при комнатной температуре зависит от процента ее концентрации 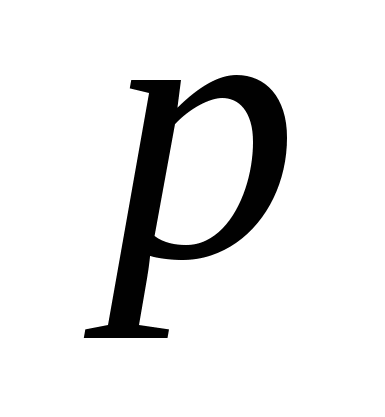 в соответствии с формулой
в соответствии с формулой 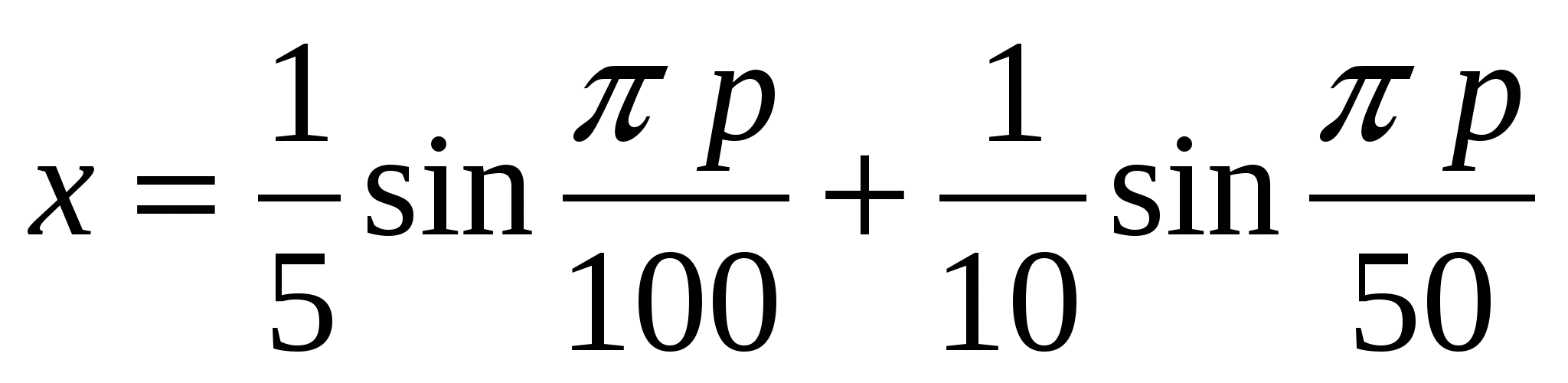 ; (
; (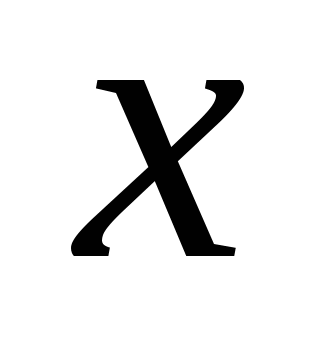 - в %;
- в %; 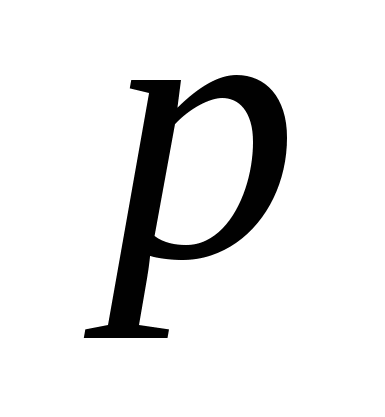 - в %). При каком значении
- в %). При каком значении 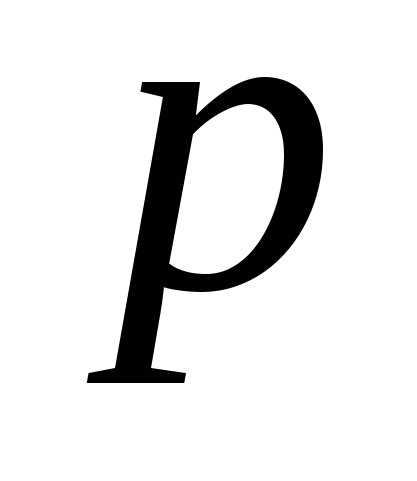 процент электропроводности
процент электропроводности 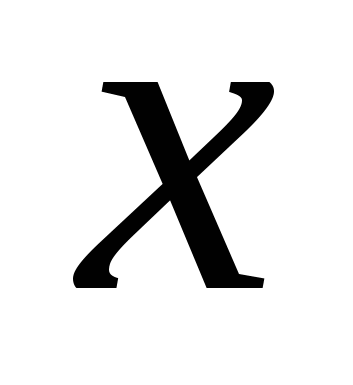 достигает наибольшего значения?
достигает наибольшего значения?
ГЕОМЕТРИЯ
-
Площадь прямоугольника 64 см2. Какую длину должны иметь его стороны, чтобы периметр был наименьшим?
Приложение 2
На предыдущем уроке были рассмотрены следующие упражнения по данной теме.
РАБОТА, ПРОИЗВОДСТВО, ТЕХНОЛОГИЯ
-
Объем произведенного товара выражается формулой
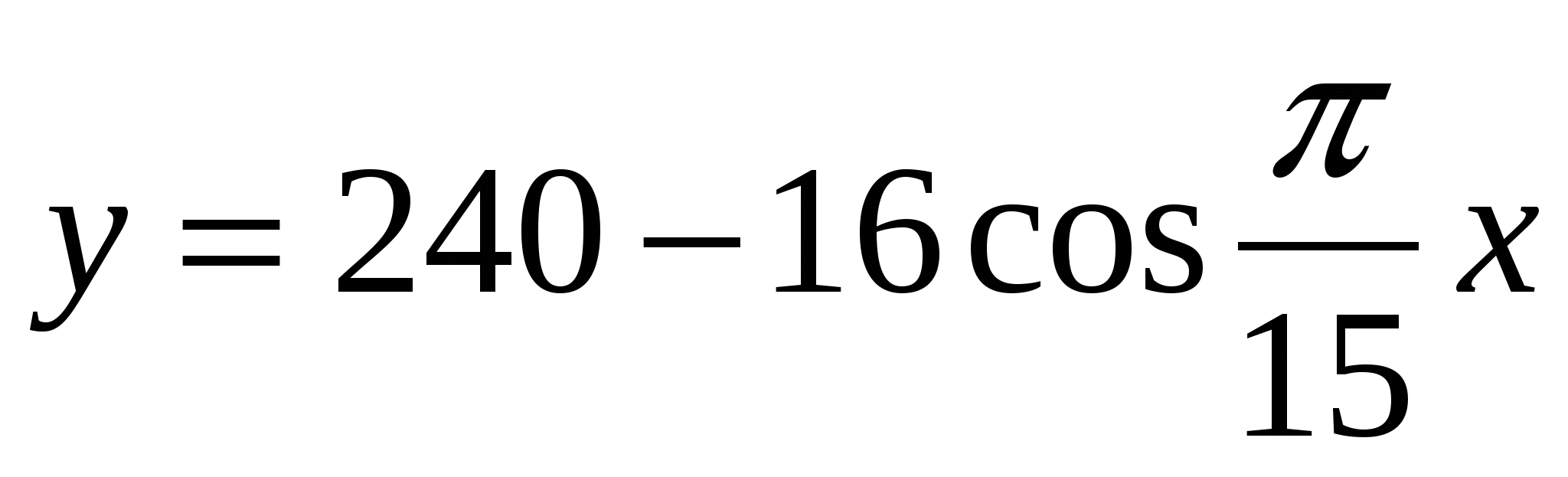 , где
, где 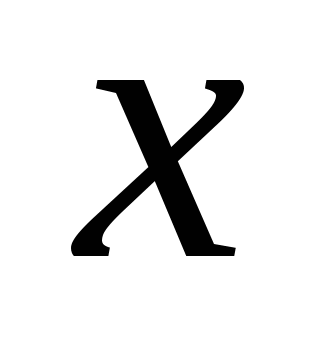 - время в сутках. Найдите скорость освоения объема работ.
- время в сутках. Найдите скорость освоения объема работ. -
Рабочий машиностроительного завода производит количество продукции, описываемое формулой
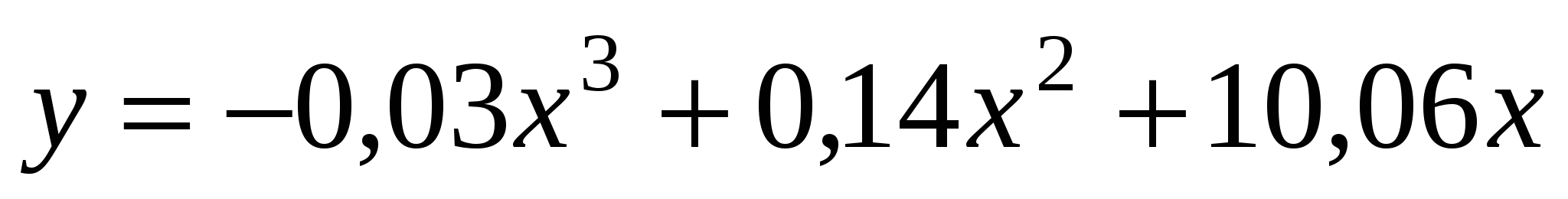 , где
, где 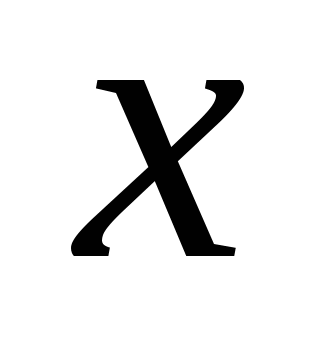 - время в часах,
- время в часах, 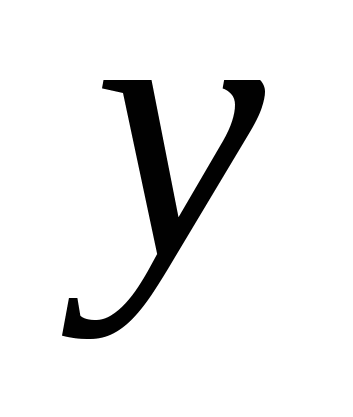 - количество продукции. Найдите дневную производительность его труда (скорость производства продукции в день).
- количество продукции. Найдите дневную производительность его труда (скорость производства продукции в день).
ФИЗИКА
-
Точка движется по закону
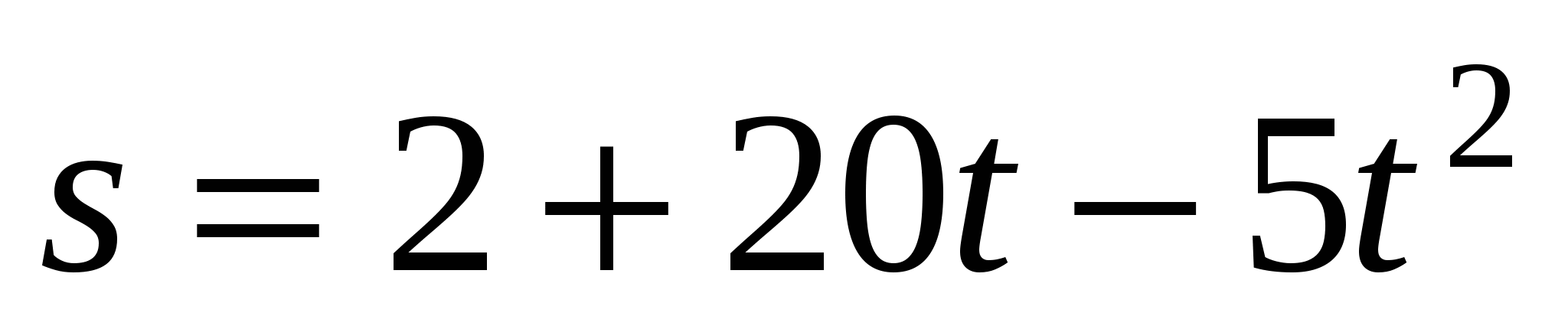 . Найдите закон, по которому меняется его скорость. Найдите закон изменения ускорения. Найдите мгновенную скорость в момент времени
. Найдите закон, по которому меняется его скорость. Найдите закон изменения ускорения. Найдите мгновенную скорость в момент времени 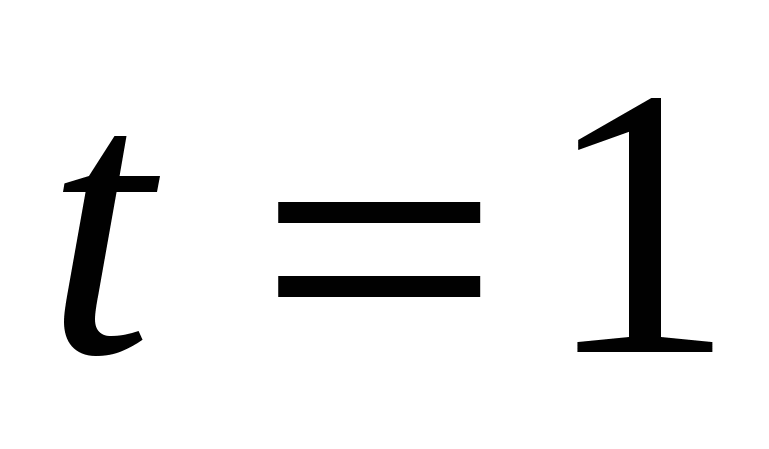 .
. -
Движение точки по оси
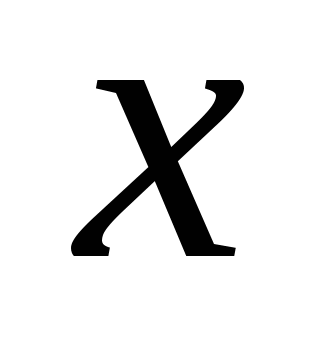 задано законом
задано законом 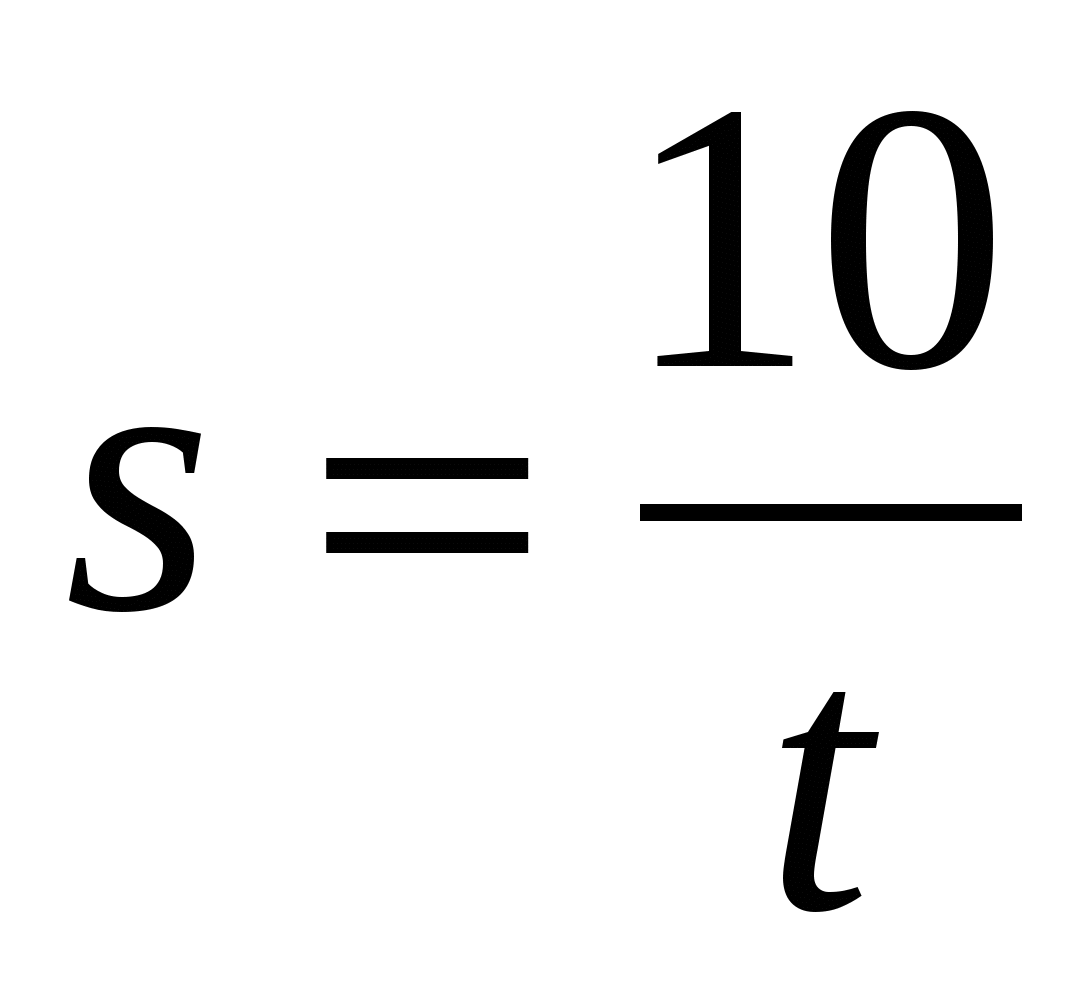 . Найдите мгновенную скорость в момент времени
. Найдите мгновенную скорость в момент времени 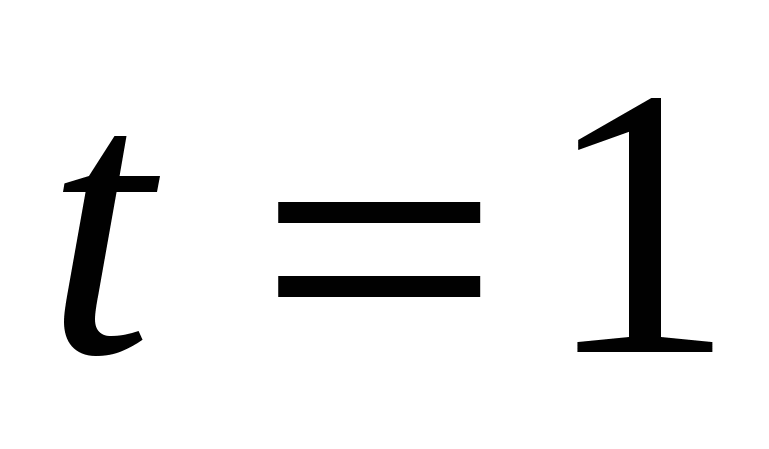 ,
, 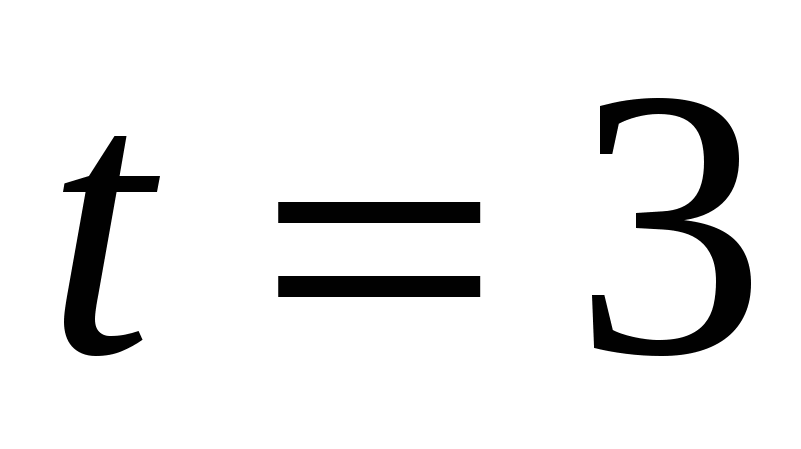 .
.
ЭКОНОМИКА
-
Отпуск товара со склада производится по закону
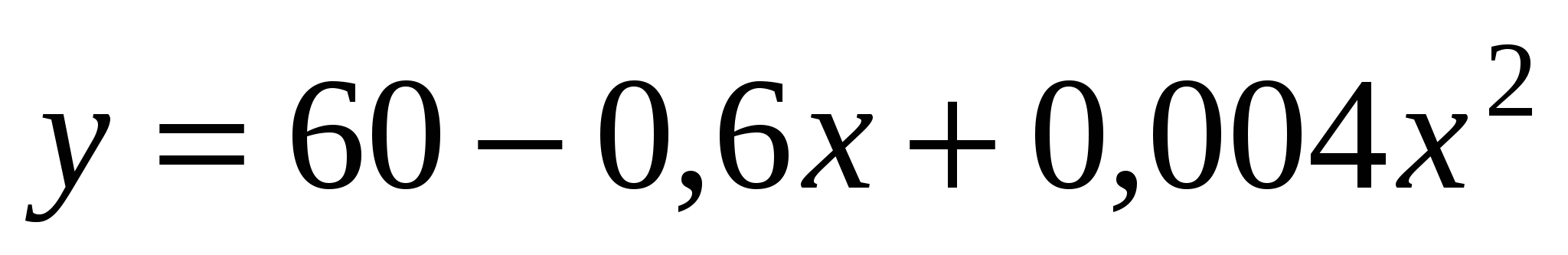 , где
, где 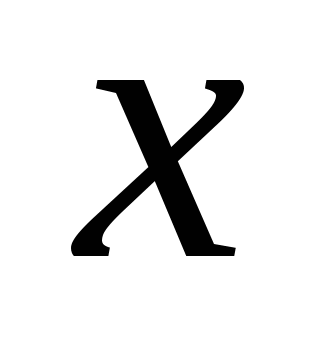 - время отпуска товара в часах. Через сколько часов скорость отпуска товара будет наименьшей.
- время отпуска товара в часах. Через сколько часов скорость отпуска товара будет наименьшей. -
Стоимость эксплуатации автомобиля, идущего со скоростью
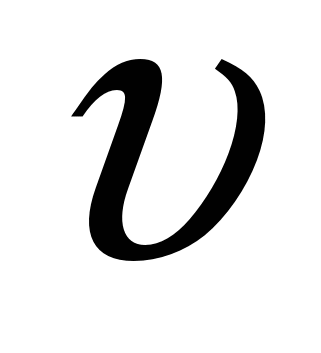 км/ч, составляет
км/ч, составляет 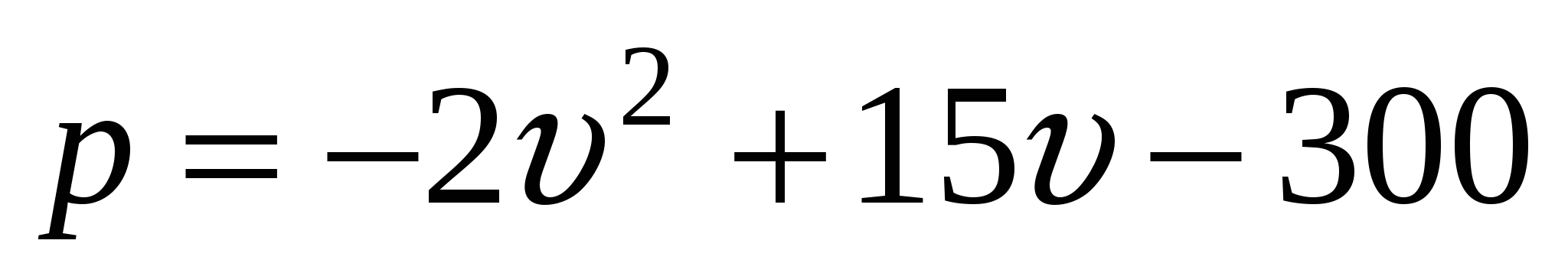 руб/ч. С какой скоростью должен идти автомобиль, чтобы стоимость 1 км пути была наибольшей?
руб/ч. С какой скоростью должен идти автомобиль, чтобы стоимость 1 км пути была наибольшей?
БИОЛОГИЯ
-
Количество зеленой массы растений в регионе изменяется по закону
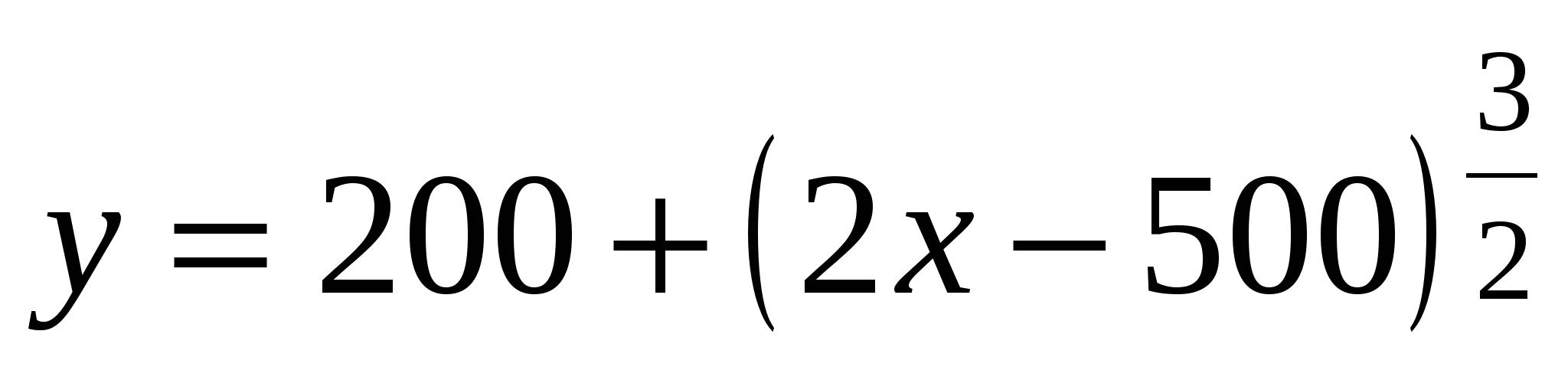 , где
, где 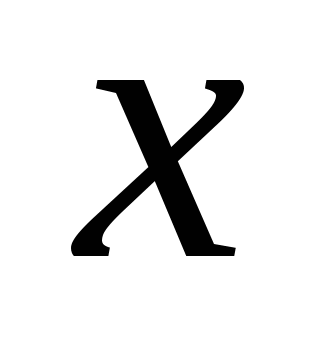 - время в годах. Через сколько лет прирост зеленой массы растений будет наименьшим.
- время в годах. Через сколько лет прирост зеленой массы растений будет наименьшим.
ГЕОМЕТРИЯ
-
Сумма длин катетов прямоугольного треугольника равна 20 см. Какой длины должны быть катеты, чтобы площадь треугольника была наибольшей?
АЛГЕБРА
-
Составьте уравнение касательной к графику функции
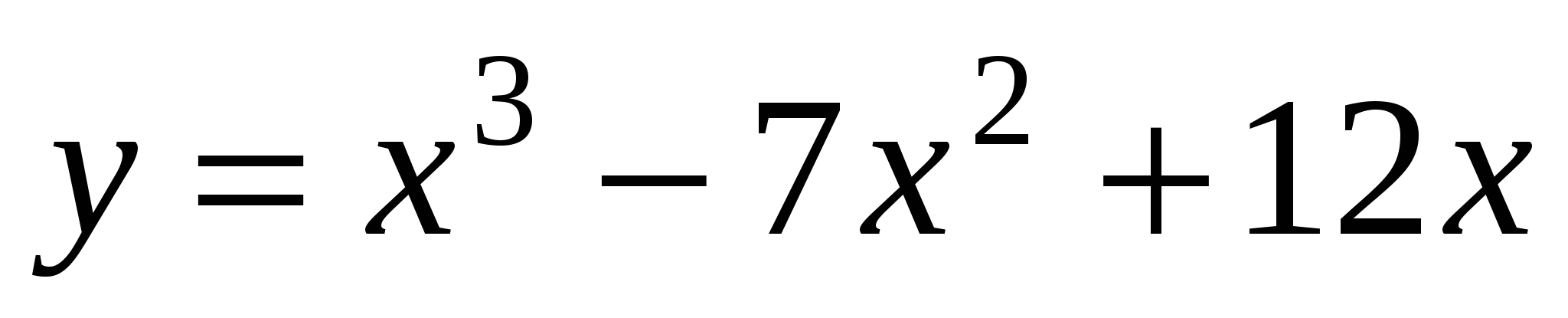 , проведенной в точке
, проведенной в точке 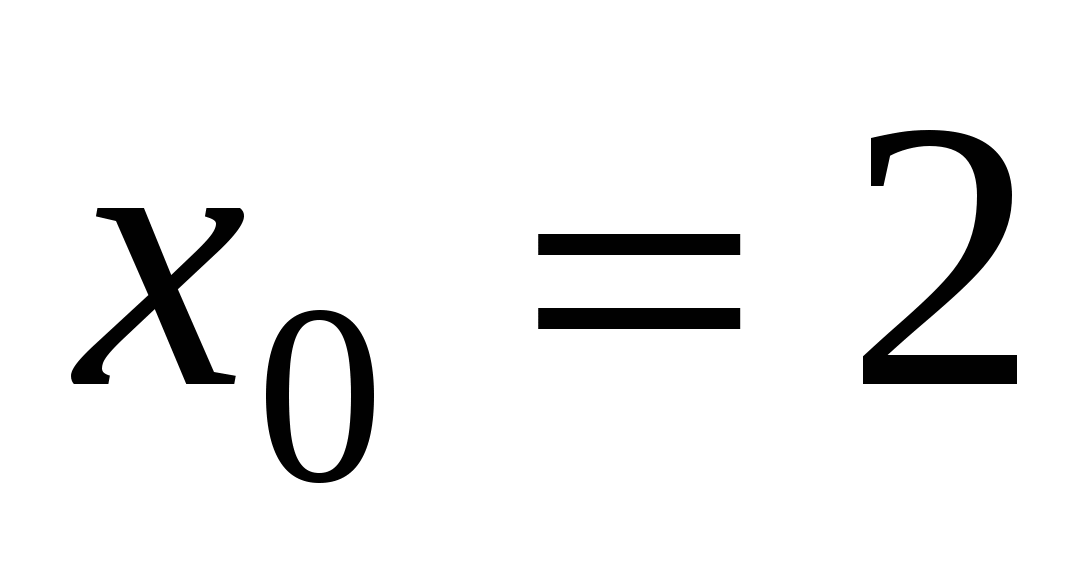 .
. -
Исследуйте функцию
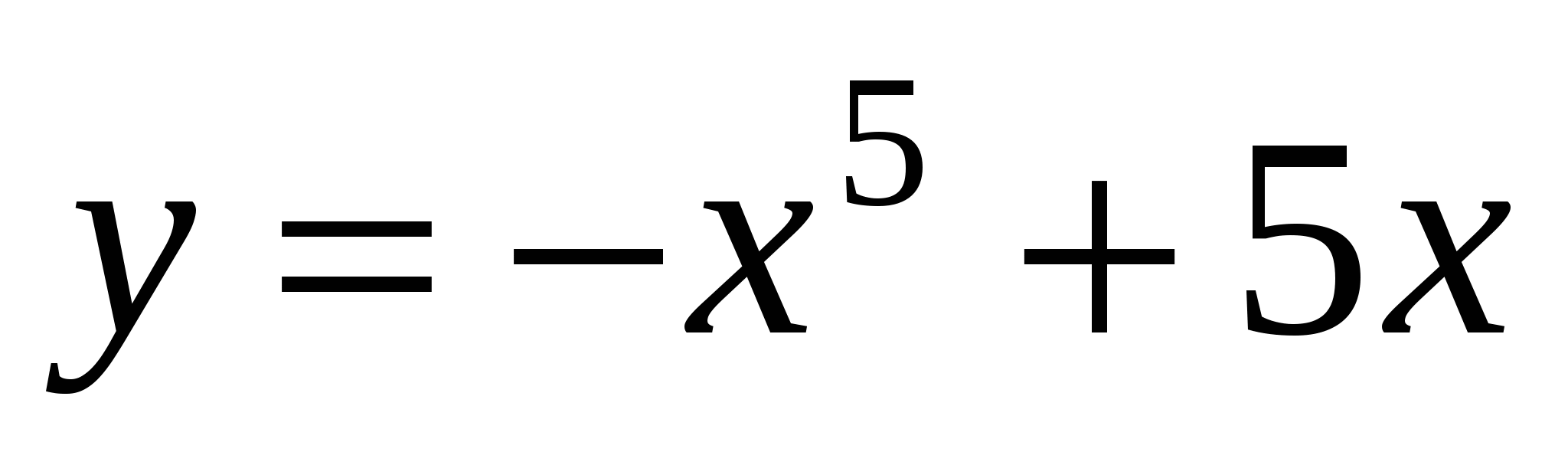 на монотонность и экстремумы.
на монотонность и экстремумы.
Литература
-
Апанасов П.Т., Апанасов Н.П.
Сборник математических задач с практическим содержанием.
Книга для учителя.
М.: Просвещение, 1987.
-
Башмаков М.И.
Математика. Учебник для профтехучилищ.
М.: Высшая школа, 1994.
-
Звавич Л.И., Аверьянов Д.И. и др.
Задания для проведения письменного экзамена по математике в 9 классе.
М.: Просвещение, 1996.
-
Мордкович А.Г., Семенов П.В.
Алгебра и начала анализа. 10 класс. В 2-х частях.
Часть 1. Учебник для общеобразовательных учреждений (профильный уровень).
Часть 2. Задачник для общеобразовательных учреждений (профильный уровень).
М.: Мнемозина, 2006.
-
Чудовский А.Н., Сомова Л.А.
Сборник заданий для проведения письменного экзамена по математике в 9 классе.
М.: Мнемозина, 1995.
Здесь представлен конспект к уроку на тему «Практические приложения производной», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (10 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

