Конспект урока «Тригонометрические уравнения» по алгебре для 10 класса

Конспект урока по алгебре в 10 классе

Автор: Березовская Дарья Ивановна

 учитель математики МБОУ «Сухинская СОШ»

Тема:  Тригонометрические уравнения

Цели урока:

• образовательные – закрепить и систематизировать виды и методы  решения тригонометрических уравнений;

• развивающие – уметь применять приемы сравнения, обобщения, выделения главного; развитие математического кругозора, мышления и речи, внимания и памяти;

• воспитательные – формирование коммуникативных способностей у учащихся.

Тип урока: урок закрепления и систематизации знаний и умений учащихся.

Методы обучения: частично – поисковый, эвристическая беседа, работа по опорным схемам, решение познавательных обобщающих задач, самопроверка.

Формы организации урока: фронтальная, групповая,  индивидуальная формы

Оборудование урока: компьютер, проектор, экран, «кубик – экзаменатор»

Структура урока:

I   Организационный момент (1 мин)

II  Математический диктант (7 мин)

III  Историческая справка (4 мин)

IV  Систематизация теоретического материала (определение видов, типов тригонометрических уравнений и методов их решения)  (7 мин)

V  Обсуждение идей решения уравнений  (10 мин)

VI  Дифференцированная самостоятельная работа  (10 мин)

VII  Домашнее задание  (2 мин)

VIII  Итог урока  (4 мин)

Ход урока.

I   Организационный момент. Объявление темы, цели урока.

II  Математический диктант. (через копирку)

Цель: контроль знаний, приведение в систему знаний по простейшим тригонометрическим уравнениям.

 I вариант

1. Чему равен  arcsin(-a)?  

2. Чему равен arcctg(-a)?

3. Каково будет решение уравнения  sin x = a  при IaI большем 1?

4. Какой формулой выражается решение уравнения sin x =  а при IaI≤ 1 ?

5. Какой формулой выражается решение уравнения   ctg х = а?

6. Каким будет решение уравнения cos x =1?

7. Каким будет решение уравнения cos x =-1?

8. Каким будет решение уравнения cos x =0?

II вариант

1. Чему равен arccos(-a) ? 

2. Чему равен arctg(-a) ?

3. Каково будет решение уравнения  cos x = a  при IaI большем 1?

4. Какой формулой выражается решение уравнения cos x = a при  IaI≤ 1?

5. Какой формулой выражается решение уравнения tgх= а?

6. Каким будет решение уравнения  sin x =1 ?

7. Каким будет решение уравнения sin x = -1?

8. Каким будет решение уравнения sin x =0?

После окончания математического диктанта собираются листочки – оригиналы (верхние), копии (нижние листы) остаются у детей. Учитель открывает правильные ответы на экране, идет самопроверка, самооценка.

Итоги математического диктанта. Выводы. (Учитель спрашивает у кого все верно, у кого 1 ошибка и т.д.)

III  Историческая справка

Выступают 2 учащихся, которые  подготовили сообщения о развитии тригонометрических уравнений.

Цель: развитие математического кругозора, воспитание интереса к математике.

IV  Систематизация теоретического материала (определение видов, типов тригонометрических уравнений и методов их решения)

Цель: Обобщение, систематизация знаний по видам, типам тригонометрических уравнений и методам их решений.

Фронтальная работа. На доске написаны уравнения:

1. sin 3x = 1

2. cos² x – 9 cos x + 8 = 0

3. 2 cos² x + 3 sin x = 0

4.  sin 2x =-  

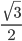
5. tg x + 3ctg x = 4

6. sin x-- 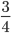  cos x = 0

7. 2 cos 3x + 4 sin x = 7

8.  (ctg x – 1)(2sin 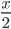 + 1) = 0

9. 6 sin ²х + 4 sin x cos x = 1

10. sin 2x – sin x = 0

      11) cos x + sin x = 2

 Учитель:                                                                                                        Ответы учащихся (примерные)

- Назовите те уравнения, которые простейшие.                                    (1, 4, 6)

- Как они решаются?                                                                                      (по известным формулам)

- Назовите одноименные уравнения и сводящиеся к ним.                (2, 3, 5, 7, 10)

- Какие уравнения из них однородные и сводящиеся к ним?             (7, 10)

- Каков общий вид однородных уравнений?                    (аcos x + вsin x = 0;   аcos² x + вsin ²x = 0 ит.д.)

- Как их решаем?                                                                              (делим  обе части на  cos x ;  cos² x и т.д.)

- Почему имеем право делить на них?            (cos x и sin x одновременно равняться нулю не могут)

- Назовите те уравнения, которые можно решить методом замены переменной.          (2, 3, 5, 10)

- Какие из этих уравнений можно решить методом разложения на множители?            (9, 11)

- Как решить уравнение № 8 ?                                                     (методом оценки левой и правой частей)

- Каким методом решить уравнение № 11 ?           (методом введения вспомогательного аргумента)

Работа в парах. Задания на карточках:  Для данных уравнений выберите соответствующий прием решения и нужную формулу, укажите их стрелкой:

Уравнения                                      Приемы, методы решения                               Формулы

2sin² х + cos x – 1 = 0                     разложение на множители                        2cos²α = 1 +  cos 2α

3sin 2x – sin 2x = 0                         понижение степени уравнения                       sin² α + cos²α= 1

4 cos² x + cos 2x = 5                        преобразование суммы                                 sin 2α = 2 sinα cosα

                                                                 в произведение

sin 7x + sinx = cos 3x                   замена переменной             

Проверка через проектор на экране.

- Сделайте выводы.

Выводы: При решении тригонометрических уравнений нет единого метода, следуя которому удалось бы решить такие уравнения. Но общая цель состоит в преобразовании входящих в уравнение выражений таким образом, чтобы рассматриваемое уравнение привелось к простейшему или распалось на несколько простейших. Ведущий принцип – не терять корни!

- На изображенных на схемах множествах точек выберите те, координаты каждого из которых удовлетворяют заданному условию:

1)  сos⁸х  + sin⁸х = 1                            

2) cos⁸х + sin⁷х = 1

3) cos⁷х+ sin⁷х = - 1

                         схема а)                                схема б)                                 схема в)

- Вопрос: Найдите соответствующую схему для уравнения     cos⁸х+ sin⁹х = 1

- Сколько таких уравнений можно составить?

Ответ: Схема а). Таких уравнений можно составить бесконечно много.

V  Обсуждение и раскрытие идей решения уравнений  (Групповая работа)

 На доске записаны 6 уравнений, каждая из 6 групп выбирает 1 уравнение, обсуждает,  решает в группе.

1. cos² x - 2 cosx = 0

2. 2 sin x cos x = 1

3. сos( 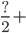x) + 3 sin x = 0

4. (2 cos x – 1) (tg x - 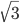) = 0

5. sin x - 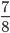 cosx = 0

6. sin² х - 5 cosx – 5 = 0

После истечения времени представители групп выходят к доске, показывают и объясняют ход решения.  Остальные группы задают вопросы и записывают решения в тетрадь.

VI  Дифференцированная самостоятельная работа

 (на выбор учащихся предлагается 3 варианта: А –на «3», В – на «4», С – на «5»)

              Вариант А                                              Вариант В                                  Вариант С

1. сosx = 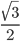                                        1) sin² х - 3 cosx = 0                      1)  8 sin² х + cosx + 1 = 0

2. 2 sin x – 1)(tg x - 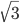) = 0            2) tg² x – 3 tg x + 2 = 0                2) 4 sin ²х + 3 sin x cos x - cos² x = 0

 Проверка самостоятельной работы осуществляется в форме самопроверки по готовым решениям на экране через проектор, оценку ставят сами ученики.

VII  Домашнее задание (на выбор учащихся) Вариант А - №23 (в,г);  Вариант В - №24 (а,г); Вариант С - №25 (в,г), 26 (а).  

VIII  Итог урока. Рефлексия. Оценки за урок, желательно всем. Вот уже несколько уроков вы решаете тригонометрические уравнения. Что это за уравнения? Какие виды тригонометрических уравнений вы знаете? Методы их решения?