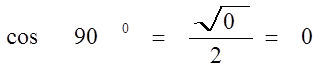
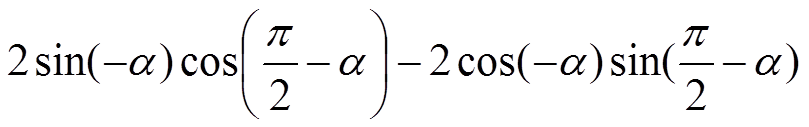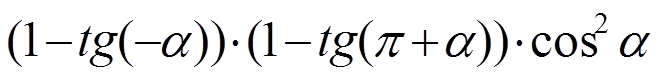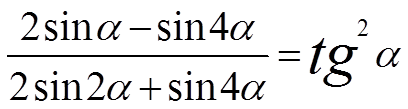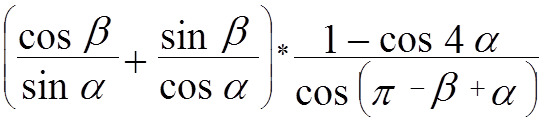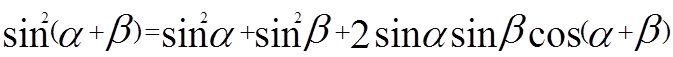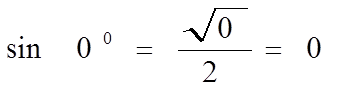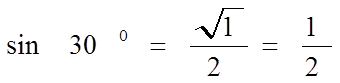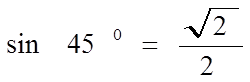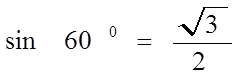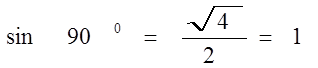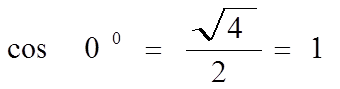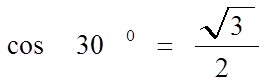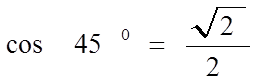Конспект урока «Тригонометрические формулы» по алгебре для 10 класса
Алгебра 10 класс.
Разработал:учитель математики первой категории
МАОУ УЛу-Юльской СОШ
Тема урока:Тригонометрические формулы
Вид урока:обобщающий.
-
Цель урока: Повторить и систематизировать изученный материал
-
Подготовиться к контрольной работе
-
Повторить определение синуса, косинуса, тангенса, котангенса числа α;
-
Повторить формулы приведения, формулы двойного угла, формулы сложения;
-
Повторить основное тригонометрическое тождество и формулы, выражающие связь между тангенсом и косинусом, между котангенсом и синусом.
-
Научить применять полученные знания при решении задач.
-
Повторить определение синуса, косинуса, тангенса, котангенса числа α;
-
Повторить формулы приведения, формулы двойного угла, формулы сложения;
-
Повторить основное тригонометрическое тождество и формулы, выражающие связь между тангенсом и косинусом, между котангенсом и синусом.
-
Научить применять полученные знания при решении задач.
Задачи урока:
-
Блиц-опрос
-
Закрепление знаний и умений
-
Закрепление знаний и умений
-
Проверка самостоятельной работы
-
Это интересно
-
Итог урока
-
Домашнее задание
Ход урока:
-
Синусом угла α называется _____ точки, полученной поворотом точки______ вокруг начала координат на угол α
-
tg α =
-
sin2 α +cos2 α=
-
1+ tg2 α=
-
sin(-α)=
-
tg (-α) =
-
cos (α+β)=
-
sin (α-β)=
-
sin 2α=
-
tg (α+β)=
-
sin(π- α)=
-
cos ( + α)=
-
Косинусом угла α называется _____ точки, полученной поворотом точки______ вокруг начала координат на угол α
-
ctg α=
-
tg α∙ ctg α=
-
1+ ctg2 α=
-
cos (-α)=
-
ctg (-α) =
-
cos (α-β)=
-
sin (α+β)=
-
cos 2α=
-
tg 2α=
-
cos(π- α)=
-
sin ( + α)=
Блиц опрос: оценка
-
«5» - 12
-
«4» - 10 – 11
-
«3» - 7 – 9
-
«2» - 0 – 6
Закрепление знаний и умений.
-
Дано
Найти
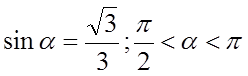
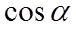
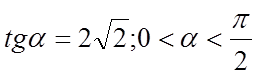
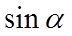
Упростить выражение:
|
|
Доказать:
Упростить:
Доказать:
Самостоятельная работа :
| Вариант2 |
Проверка.
Зарождение тригонометрии относится к глубокой древности. Само название «тригонометрия» греческого происхождения, обозначающее.
Одним из основоположников тригонометрии считается древнегреческий астроном Гиппарх, живший во 2 веке до нашей эры. Гиппарх (Hípparchos) (около 180—190 до н. э., Никея, — 125 до н. э., Родос), древнегреческий учёный.
Одним из основоположников тригонометрии считается древнегреческий астроном Гиппарх, живший во 2 веке до нашей эры. Гиппарх (Hípparchos) (около 180—190 до н. э., Никея, — 125 до н. э., Родос), древнегреческий учёный.
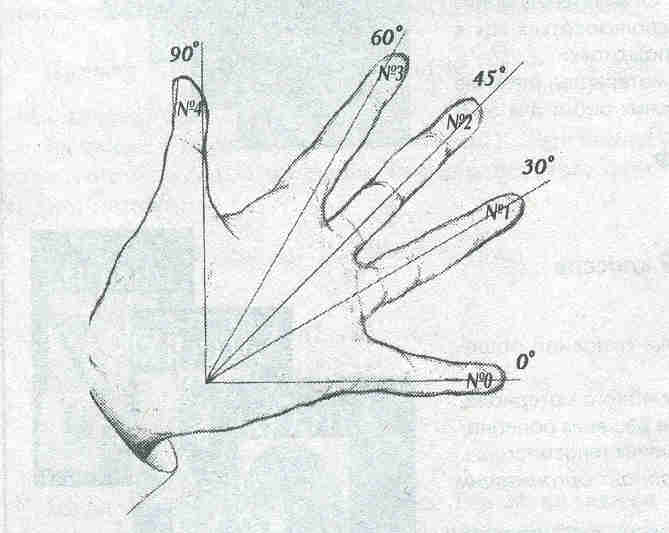
№0 Мизинец 00
№1 Безымянный 300
№2 Средний 450
№3 Указательный 600
№4 Большой 900
sin α =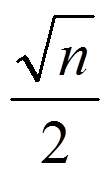
Значение синуса.
| Угол α | | |
| 0 | 0 |
|
| 1 | 30 |
|
| 2 | 45 |
|
| 3 | 60 |
|
| 4 | 90 |
|
Значения косинуса.
| угол | | |
| 4 | 0 |
|
| 3 | 30 |
|
| 2 | 45 |
|
| 1 | 60 |
|
| 0 | 90 |
|
Домашнее задание.
Здесь представлен конспект к уроку на тему «Тригонометрические формулы», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (10 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.